文章目录
- 写在前面
- 快速排序的基本体系
- 快速排序的优化
- 快速排序的非递归实现
- 排序分类总结
- 插入排序
- 选择排序
- 交换排序
- 归并排序
写在前面
快速排序作为效率相当高的排序算法,除了对于特殊数据有其一定的局限性,在大多数应用场景中都有它特有的优势和应用,前面文章有对快速排序做总结,但实际上快速排序由于它广泛的应用和特殊的优势,应当值得单独拿来仔细琢磨分析,因此这篇主要对快速排序的各种细节进行打磨和分析,加深印象也能不断提升效率,打开思维举一反三用到更多的场景中
快速排序的基本体系
在进行快速排序的优化前,先进行一些回忆快速排序的方法,有利于后续对快速排序的总结
首先这里先介绍的都是递归形式的快速排序,从大的方向来看,快速排序实现是很简单的,需要借助一个让数据分布在某一值两侧的算法,再在此基础上递归到左边和右边即可,那么基本框架就是下面的这样:
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = Partsort(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
而上面的算法有三种,分别是hoare算法,挖坑算法,前后指针算法,这三种都能完成快速排序,这里只介绍其中一种前后指针法,掌握一种即可让快速排序跑起来,完成我们对它的目标
下面进行前后指针法
前后指针法可以通俗的认为,cur在前面探路,只要遇到一个比key小的数字就把这个数字扔到后面,最后再把key往前放
int Partsort(int* a, int left, int right)
{
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
prev++;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
快速排序的优化
下面我用leetcode中的一道题进行分析快速排序的多种优化
leetcode – 数组排序
首先,我们把上面的代码放上去,显然leetcode不会允许你这么简单的就通过测试

这里观察发现,过不去的原因是快速排序对于keyi的选择是很重要的,如果keyi恰好选到了最小的一个值,那么时间复杂度一下变成O(N^2),回到上面的测试样例看,如果测试样例让keyi每次都选了最小的,时间复杂度回到了冒泡排序一个级别的效率,很显然是过不了的,那么我们的第一步优化就是让keyi的选择发生一些改变
int GetMid(int* a, int left, int right)
{
int midi = (left + right) / 2;
if (a[left] < a[midi])
{
if (a[midi] < a[right])
{
return midi;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[midi]
{
if (a[midi] > a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
int Partsort(int* a, int left, int right)
{
int midi = GetMid(a, left, right);
Swap(&a[midi], &a[left]);
int cur = left + 1;
int prev = left;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = Partsort(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
嗯,看起来这次靠谱了不少,这样的话对key的选择就相对随机了一点,再跑一次试试看

但依旧被卡住了,那这如何处理?究其原因还是因为这是题目的数据对快速排序进行了特殊照顾,破局的方法也是有的,利用rand随机值处理一下
void Swap(int* p, int* c)
{
int tmp = *p;
*p = *c;
*c = tmp;
}
int GetMid(int* a, int left, int right)
{
//int midi = (left + right) / 2;
int midi = left+(rand() % (right-left));
if (a[left] < a[midi])
{
if (a[midi] < a[right])
{
return midi;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[midi]
{
if (a[midi] > a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
int Partsort(int* a, int left, int right)
{
int midi = GetMid(a, left, right);
Swap(&a[midi], &a[left]);
int cur = left + 1;
int prev = left;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = Partsort(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
但似乎并不奏效,最后还是会被卡住,这里出现问题的原因很简单,如果全是一个数字,快速排序依旧不占优,这里就引入了第三次优化,叫三路划分

三路划分:
主要针对的就是这样的情况,解决的原理就是把定义left cur right指针,如果cur指向的内容比key大,就和left进行交换,如果cur的值和key的值相等就继续向后遍历,如果cur的值大于key,就和right进行交换,由于不知道right换过来的值是多少,但可以保证right此时的值一定是大于key的,因此只需要让right–即可
那么代码实现就可以改成这样
int Partsort(int* a, int left, int right)
{
int cur = left + 1;
int key = a[left];
while (cur <= right)
{
if (a[cur] < key)
{
Swap(&a[cur], &a[left]);
cur++;
left++;
}
else if (a[cur] > key)
{
Swap(&a[cur], &a[right]);
right--;
}
else
{
cur++;
}
}
return left;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = Partsort(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
这样就能解决问题了
由此可见,快速排序从最初版本到可优化版本之间有很多优化点,也侧面反映出快速排序实际上是一个不算稳定的排序,在许多特定的算法下它并不适合
快速排序的非递归实现
快速排序是利用递归实现的,而凡是递归就有可能爆栈的情况出现,因此这里要准备快速排序的非递归实现方法
非递归实现是借助栈实现的,栈是在堆上malloc实现的,栈区一般在几十Mb左右,而堆区有几G左右的空间,在堆上完成操作是没有问题的
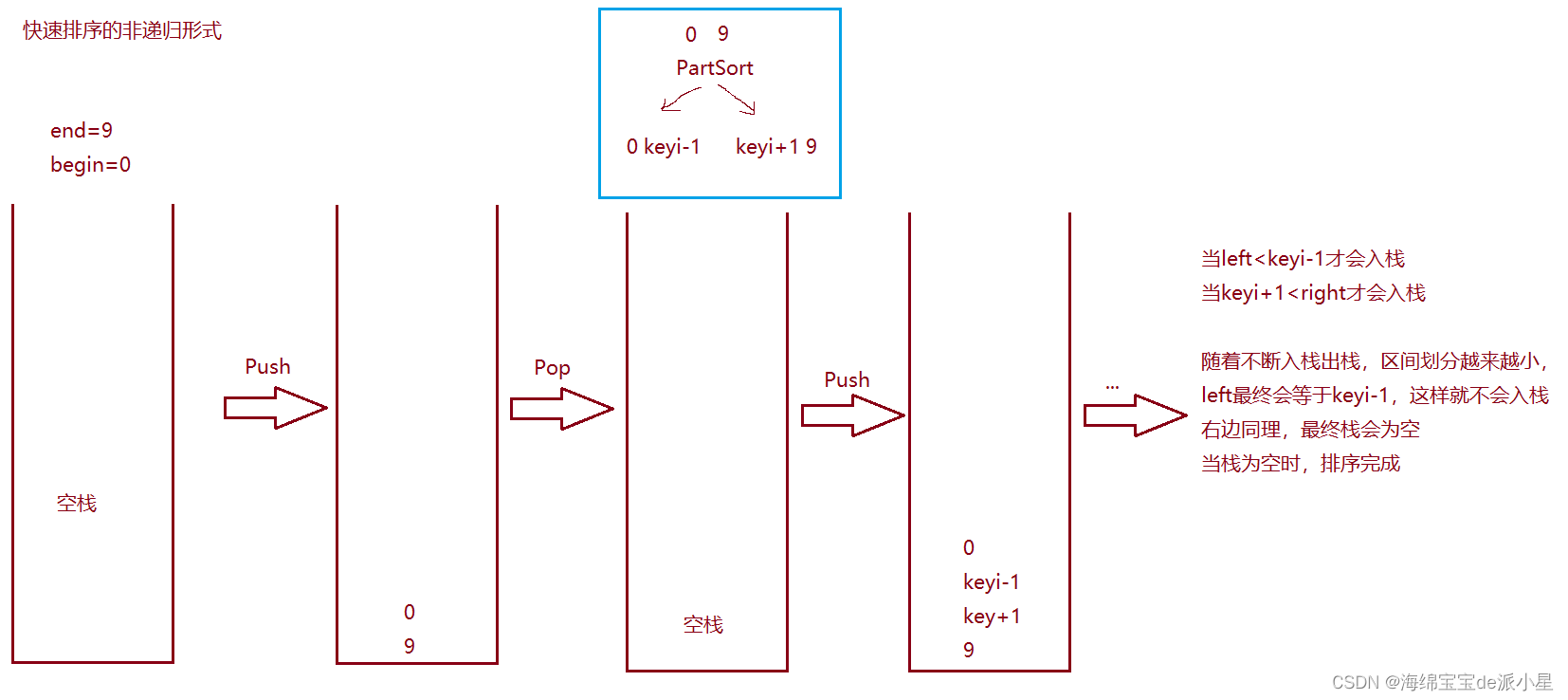
当left<keyi-1才会入栈,当keyi+1<right才会入栈
随着不断入栈出栈,区间划分越来越小,left最终会等于keyi-1,这样就不会入栈,右边同理,不入栈只出栈,最终栈会为空,当栈为空时,排序完成
后续STL中用栈可以很方便表示
排序分类总结
插入排序
插入排序:有直接插入和希尔排序,其中希尔排序是在直接插入的基础上衍生而来的
先说插入排序原理:从前向后遍历,如果遍历的数字比前面的数字小,就继续和前面的前面的数字比,直到该数字比前面的数字大,那么再让比它大的数字向后挪,它本身插入到这当中即可
再说希尔排序原理:希尔排序是在插入排序的基础上衍生出来的,原理是先进行预排序,再进行插入排序,直接插入排序对于数据差异很大的数据表现并不好,因此希尔排序先把数据进行一个预排序,再进行插入排序效果就会好很多
选择排序
选择排序:原理是每次排序都能选出一个最值,这样经过N次后就可以选出每次的最值,这样就能把数据排好,选择排序分为选择排序和堆排序
先说普通的选择排序:就是直接进行选择,效率较差,时间复杂度也很高
再说堆排序:要利用的是一种特殊的数据结构–堆,通过这个数据结构可以把数组中的元素搭建成堆的模型,再用堆的模型选出最大值,放到最后的位置,再重新调整堆,找出新的最大值,依次类推就可以找到正确的顺序,完成一组数的正确排序
交换排序
交换排序分为冒泡排序和快速排序,其中快速排序是比较好用的排序
先说冒泡排序:效率比普通插入排序高一点,冒泡排序的基本原理是把每次进行两两元素的交换,这样可以把一个最大的元素交换到末尾,再进行第二次交换,直到把所有元素按顺序交换到最后,这样就实现了排序的基本功能
再说快速排序:效率是很可观的,基本原理是利用递归的思想,把数据进行分割,选出一个关键数,让所有数字中比关键数大的排在关键数右边,比关键数小的排在关键数左边,再分别到左边和右边进行分割,直到分割的区域足够小,这样就能保证左边中间右边有序,每个区间都这样做,就能保证最终的区间是有序的,这样就能完成快速排序
归并排序
归并排序也是利用了递归的思想,把数字全部拆成零散的数据,再把这些数据都组合起来即可