目录
【案例1】
【题目描述】
【思路解析】
【代码实现】
【案例2】
【题目描述】
【思路解析】
【代码实现】
【案例3】
【题目描述】
【思路解析】
【案例4】
【题目描述】
【思路解析】
【代码实现】
【案例5】
【题目描述】
【子序列概念】
【思路解析1 经典方法 时间复杂度为O(N^2)】
【代码实现1】
【思路解析2 优化技巧之构建单调性 时间复杂度为O(N*logN)】
【代码实现2】
【案例6】
【题目描述】
【思路解析】
【代码实现】
【案例1】
【题目描述】

【思路解析】
一个简单的贪心策略。
对于字符串str,任意一个位置上只能为字符'.'或者'X'。则对于任意i位置有两种情况。
(1)i位置上为字符'X',此位置不需要放路灯
(2)i位置上为字符'.',此位置放灯则需要根据i+1位置来判断,如果i+1位置是‘X',则i位置放灯,如果i+1位置是’.',则i+1位置放灯。
【代码实现】
import java.util.Scanner;
/**
* @ProjectName: study3
* @FileName: Ex1
* @author:HWJ
* @Data: 2023/7/30 9:27
*/
public class Ex1 {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int t = input.nextInt();
for (int i = 0; i < t; i++) {
int n = input.nextInt();
String s = input.nextLine();
System.out.println(minLight(s, n));
}
}
public static int minLight(String s, int length) {
if (s == null || length == 0) {
return 0;
}
char[] str = s.toCharArray();
int i = 0;
int count = 0;
while (i < length) {
if (str[i] == 'X') {
i++;
} else {
count++;
// 加入条件(i + 1) < length 来防止越界
if ((i + 1) < length && str[i + 1] == 'X') {
i += 2;
} else if ((i + 1) < length && str[i + 1] == '.') {
i += 3;
}else { // 如果不是以上两种情况 就说明 i+1 == length,说明已经遍历完成,直接退出循环
break;
}
}
}
return count;
}
}【案例2】
【题目描述】

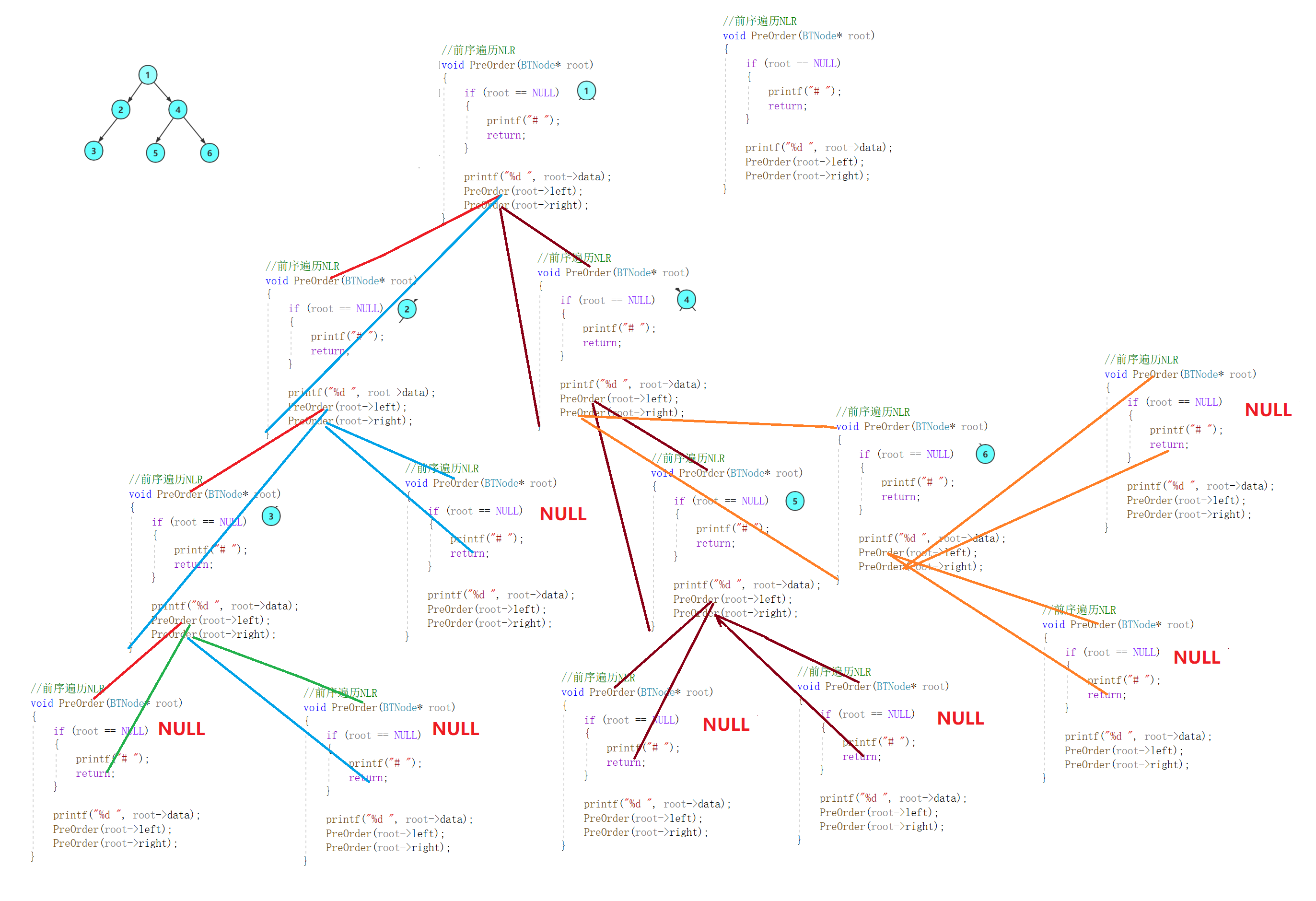
【思路解析】
我们已知先序数组int[ ] pre,中序数组int[ ] in,我们需要得到后序数组int[ ] pos,先序数组和中序数组和后序数组长度相同,然后先序数组对应二叉树的顺序为头左右,中序数组对应二叉树的顺序为左头右,后序数组对应二叉树的顺序为左右头,所以我们可以通过先序数组的第一个位置确定整棵树的头,然后找出它在中序数组的位置,此位置左边就是整棵树最大的左子树,右边就是整棵树最大的右子树,然后在先序数组中头位置的右边同样多的数也是左子树,然后剩下的数为右子树,这样又可以继续递归确定子树的位置然后将其填入后序数组中。填入时,头位置填入在当前填充后序数组位置中最后一个,然后填入右子树,然后填入左子树,填入顺序为从右至左。
【代码实现】
代码中在中序数组中寻找头的位置使用的是遍历的方式,我们可以对中序数组中每个位置上的值做一个哈希表来对应,这样下次寻找头的时候直接访问哈希表即可,创建哈希表只需要做一次遍历,所以这是一个优化搜索的方法。
import java.util.Arrays;
/**
* @ProjectName: study3
* @FileName: Ex2
* @author:HWJ
* @Data: 2023/7/30 10:16
*/
public class Ex2 {
public static void main(String[] args) {
int[] pre = {1,2,4,5,3,6,7};
int[] in = {4,2,5,1,6,3,7};
int[] pos = getPosArray(pre, in);
System.out.println(Arrays.toString(pos));
}
public static int[] getPosArray(int[] pre,int[] in){
int N = pre.length;
int[] pos = new int[N];
process(pre, 0, N - 1, in, 0, N - 1, pos, 0, N - 1);
return pos;
}
public static void process(int[] pre, int prei, int prej,
int[] in, int ini, int inj,
int[] pos, int posi, int posj){
if (prei > prej){
return;
}
pos[posj] = pre[prei];
int find = ini;
for (; find < inj; find++) {
if (in[find] == pre[prei]){
break;
}
}
process(pre, prei + 1 + find - ini, prej, in, find + 1, inj, pos, posj - (find - ini), posj - 1);
process(pre, prei + 1, prei + find - ini, in, ini, find - 1, pos, posi, posi - 1 + (find - ini));
}
}
【案例3】
【题目描述】
将一个数字用中文表示出来,表示规则需要满足中国人的读数习惯。
经考查 15中国人习惯读十五,215习惯读二百一十五(个别省份读两百一十五),1017习惯读一千零十七,1215习惯读一千二百一十五,所以十位前读不读1,取决于有没有百位。
【思路解析】
纯coding问题,但是有一个策略,可以先完成1-10的发言,再完成1-99,在完成1-999,后面依次累加,完成全部。
【案例4】
【题目描述】

【思路解析】
如果使用遍历的话完全能得到个数,但时间复杂度为O(N),所以我们需要利用完全二叉树的特性来进行优化,时间复杂度可以达到O((logN)^2)。

【代码实现】
/**
* @ProjectName: study3
* @FileName: Ex4
* @author:HWJ
* @Data: 2023/7/30 11:17
*/
public class Ex4 {
public static void main(String[] args) {
}
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
}
// 请保证以head为头的树是一颗完全二叉树。
public static int nodeNum(Node head) {
if (head == null) {
return 0;
}
return bs(head, 1, mostLeftLevel(head, 1));
}
// level 表示node节点所在层数, h表示整棵树的深度
public static int bs(Node node, int level, int h) {
if (level == h) {
return 1;
}
if (mostLeftLevel(node.right, level + 1) == h) {
// 如果mostLeftLevel(node.right, level + 1) == h,即右子树的最左节点到了h层说明左子树一定是一个满二叉树。
// 否则说明右子树是一个满二叉树。
return (1 << (h - level)) + bs(node.right, level + 1, h);
} else {
return (1 << (h - level - 1)) + bs(node.left, level + 1, h);
}
}
// 求出此节点在这棵树上的最左节点的层数
// L表示node在的层数
// 以node为节点的整棵树应该满足完全二叉树的定义
public static int mostLeftLevel(Node node, int L) {
while (node.left != null) {
L++;
node = node.left;
}
return L;
}
}
【案例5】
【题目描述】

【子序列概念】
子序列是指一个序列中任意选取若干个元素(可以是相邻的元素,也可以是不相邻的元素)组成的序列。这些元素的原先相对顺序保持不变。例如,对于序列 [1, 2, 3, 4],其子序列可以是 [1, 2, 3]、[1, 4]、[2, 4]、[1, 3, 4] 等等。在算法和数据结构中,子序列广泛用于字符串匹配、最长子序列等问题的求解。
【思路解析1 经典方法 时间复杂度为O(N^2)】
生成一个与数组arr等长的数组dp,dp[i]的含义为以arr[i[为结尾的子序列最长长度为多少。这样对于任意位置i,它前面的位置已经形成了它的最长递增子序列,然后我们以i位置的数字结尾,我们只需要找到0 --- i-1位置上小于i位置数字的最优解作为倒数第二个数字即可(如果找不到这样的第二个数字,这dp[i]填充1),这样就可以完成对dp数组的填充。然后找出dp数组中最大的那个,我们便得到了最长递增子序列的长度。
【代码实现1】
/**
* @ProjectName: study3
* @FileName: Ex5
* @author:HWJ
* @Data: 2023/7/30 12:58
*/
public class Ex5 {
public static void main(String[] args) {
int[] arr = {6, 1, 5, 2, 7, 3, 4};
System.out.println(getMaxSub(arr));
}
public static int getMaxSub(int[] arr) {
int N = arr.length;
int[] dp = new int[N];
for (int i = 0; i < N; i++) {
dp[i] = 1; //初始化为1,不管后面是否能找到,都能得到正确的dp结果
for (int j = i - 1; j >= 0; j--) {
if (arr[i] > arr[j]) { // 找到0 --- i-1位置上小于i位置数字的最优解作为倒数第二个数字
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int max = dp[0];
for (int i = 1; i < N; i++) {
max = Math.max(max, dp[i]);
}
return max;
}
}
【思路解析2 优化技巧之构建单调性 时间复杂度为O(N*logN)】
构建一个等长的ends数组,刚开始里面数据全是无效区域,然后遍历arr数组每个数字,然后在ends数字的有效区域中找到大于这个数字的最左位置,然后更新这个位置上的数字,如果找不到这个数字,则扩充有效区域,然后将这个数字更新到有效区域上,因为这个数组满足单调性,所以在ends数组遍历时可以使用二分法,使遍历的时间复杂度为O(logN)。然后确定了这个数字的在ends上的所在位置后如果该位置假设为i位置,则以它为结尾的最长递增子序列的长度为i+1。
但是如果我们只需要得到最长递增子序列的长度,而不需要知道以arr每个数字结尾的最长递增子序列的长度,我们便可以不再构造dp数组,而是将ends的有效区域长度作为最优解返回。
即代码2的返回修改为 return right + 1;
【代码实现2】
/**
* @ProjectName: study3
* @FileName: Ex6
* @author:HWJ
* @Data: 2023/7/30 13:15
*/
public class Ex6 {
public static void main(String[] args) {
int[] arr = {6, 1, 5, 2, 7, 3, 4};
System.out.println(getMaxSub(arr));
}
public static int getMaxSub(int[] arr) {
int N = arr.length;
int[] dp = new int[N];
int[] ends = new int[N];
int left = 0;
int right = 0;
ends[0] = arr[0];
dp[0] = 1;
for (int i = 1; i < N; i++) {
int index = getIndex(ends, left, right, arr[i]);
if (index == -1){
ends[++right] = arr[i];
dp[i] = right + 1;
}else {
ends[index] = arr[i];
dp[i] = index + 1;
}
}
int max = Integer.MIN_VALUE;
for (int i = 0; i < N; i++) {
max = Math.max(dp[i], max);
}
return max;
}
// 这里的left和right与上面的left和right同义,代表ends数组的有效区域,范围为[left,right]
// 返回ends数组中,大于num的最左数字的索引
// 如果返回的索引为-1,则没有找到比num大的数字,则需要扩充ends数组的有效区域,然后更新数组,否则直接根据索引进行更新
public static int getIndex(int[] ends, int left, int right, int num){
int index = -1;
while(left <= right){
int mid = (left + right) / 2;
if (ends[mid] > num){
right = mid - 1;
index = mid;
}else {
left = mid + 1;
}
}
return index;
}
}
【案例6】
【题目描述】

【思路解析】
如果n=13,则这个数字为12345678910111213,然后他能不能被3整除可以转化为(1+2+3+4+5+6+7+8+9+1+0+1+1+1+2+1+3)能不能被3整除,然后10能不能被3整除又可以转化为1+0能不能被3整除,所以我们可以将(1+2+3+4+5+6+7+8+9+1+0+1+1+1+2+1+3)这里的数字作同语替换改为(1+2+3+4+5+6+7+8+9+10+11+12+13),这就可以转为 ((n * (n+1))/2)%3,然后防止((n * (n+1))/2)过大,所以使用long来存放
【代码实现】
import java.util.Scanner;
/**
* @ProjectName: study3
* @FileName: Ex7
* @author:HWJ
* @Data: 2023/7/30 14:00
*/
public class Ex7 {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int l =input.nextInt();
int r = input.nextInt();
int count = 0;
for (int i = l; i <= r; i++) {
long s = ((long) (i + 1) * i) / 2;
if (s % 3 == 0){
count++;
}
}
System.out.println(count);
}
}