文章目录
- 动态规划(子数组系列)
- 1. 最大子数组和
- 2. 环形子数组的最大和
- 3. 乘积最大子数组
- 4. 乘积为正的最长子数组的长度
- 5. 等差数列划分
- 6. 最长湍流子数组
- 7. 单词拆分
- 8. 环形字符串中的唯一的子字符串
动态规划(子数组系列)
1. 最大子数组和
题目链接
-
状态表示
dp[i]表示到 i 位置时所有子数组的最大和如下展示的这样:

-
状态转移方程

-
初始化
为了方便初始化,采用虚拟节点的方式,这里初始化
dp[0] = 0 -
填表
从左到右
-
返回值
由于每个dp表里的每个值都表示到这个位置的最大子数组的和,所有需要返回最大值
AC代码:
class Solution
{
public:
int maxSubArray(vector<int>& nums)
{
int n = nums.size();
vector<int> dp(n + 1);
int ret = -0x3f3f3f3f;
for (int i = 1; i <= n; i++)
{
dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
ret = max(ret, dp[i]);
}
return ret;
}
};
2. 环形子数组的最大和
题目链接
分析题目:这道题目可以取环形数组,是不是可以像之间做的环形的打家劫舍题目一样来解决?
还是分为两种情况来考虑:

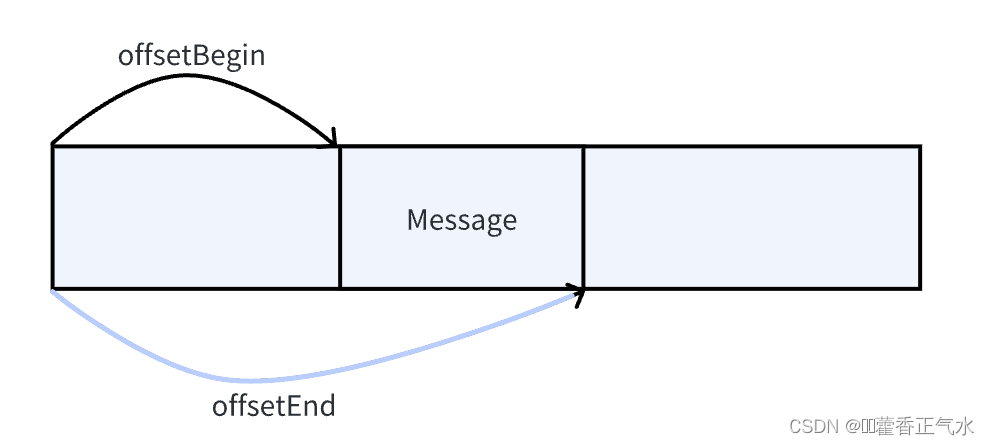
如果最大和是蓝色区域的部分,只需要求出最大子数组的和就可以
如果是这样,由于数组整体的和是固定的,只需要求出中间的最小值然后相减即可
-
状态表示
讲过前面的题目分析,发现这个题目需要两个状态表示:
f[i]表示到 i 位置时所有子数组,子数组和最大的值g[i]表示到 i 位置时所有子数组,子数组和最小的值 -
状态转移方程

-
初始化
采用虚拟节点的方式
-
填表
-
返回值
返回两种情况的较大值
AC代码:
class Solution
{
public:
const int N = 0x3f3f3f3f;
int maxSubarraySumCircular(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
int fMax = -N, gMin = N, sum = 0;
for (int i = 1; i <= n; i++)
{
f[i] = max(nums[i - 1], f[i - 1] + nums[i - 1]);
fMax = max(fMax, f[i]);
g[i] = min(nums[i - 1], g[i - 1] + nums[i - 1]);
gMin = min(gMin, g[i]);
sum += nums[i - 1];
}
if (sum == gMin) return fMax;
else return max(fMax, (sum - gMin));
}
};
3. 乘积最大子数组
题目链接
-
状态表示
f[i]表示以 i 为结尾所有子数组中最大乘积g[i]表示以 i 为结尾所有子数组中最小乘积 -
状态转移方程

-
初始化
虚拟节点的方式,为了不影响后续的填表采用
f[0] = 1, g[0] = 1 -
填表
从左到右
-
返回值
返回乘积最大的即可
AC代码:
class Solution
{
public:
int maxProduct(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
f[0] = g[0] = 1;
int ret = -0x3f;
for (int i = 1; i <= n; i++)
{
if (nums[i - 1] < 0)
{
f[i] = g[i - 1] * nums[i - 1];
g[i] = f[i - 1] * nums[i - 1];
}
if (nums[i - 1] > 0)
{
f[i] = f[i - 1] * nums[i - 1];
g[i] = g[i - 1] * nums[i - 1];
}
f[i] = max(nums[i - 1], f[i]);
g[i] = min(nums[i - 1], g[i]);
ret = max(ret, f[i]);
}
return ret;
}
};
4. 乘积为正的最长子数组的长度
题目链接
-
状态表示
f[i]表示:以 i 位置为结尾所有子数组中乘积为正数的最大长度g[i]表示:以 i 位置为结尾所有子数组中乘积为负数的最大长度 -
状态转移方程
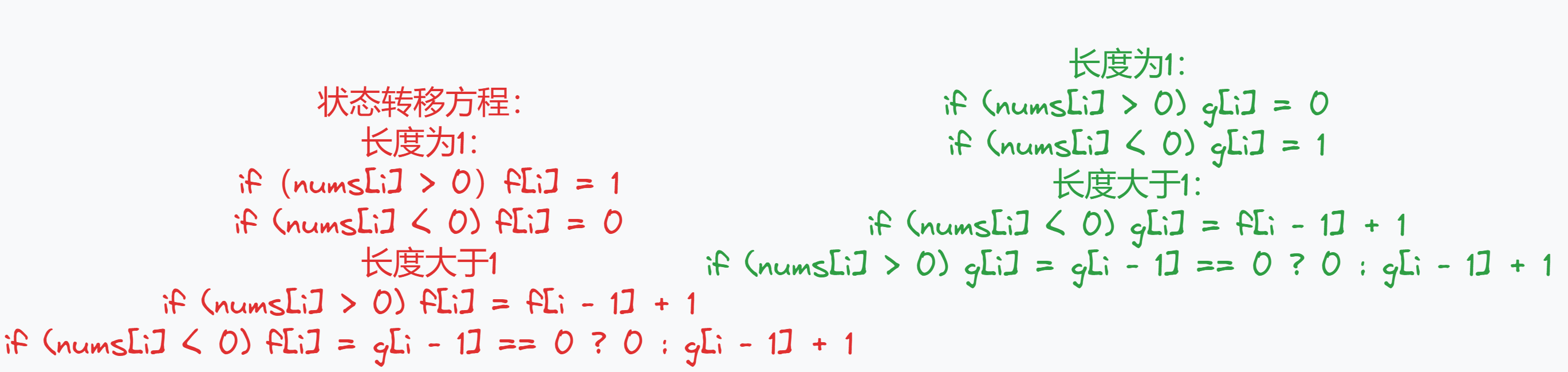
-
初始化
f[0] = 1, g[0] = 0 -
填表
-
返回值
返回乘积为正的最大长度
AC代码:
class Solution
{
public:
int getMaxLen(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
int ret = -0x3f3f3f3f;
for (int i = 1; i <= n; i++)
{
if (nums[i - 1] > 0)
{
f[i] = max(1, f[i - 1] + 1);
g[i] = max(0, g[i - 1] == 0 ? 0 : g[i - 1] + 1);
}
if (nums[i - 1] < 0)
{
f[i] = max(0, g[i - 1] == 0 ? 0 : g[i - 1] + 1);
g[i] = max(1, f[i - 1] + 1);
}
ret = max(ret, f[i]);
}
return ret;
}
};
5. 等差数列划分
题目链接
-
状态表示
dp[i]表示到 i 位置时,所有是等差数列子数组之和 -
状态转移方程
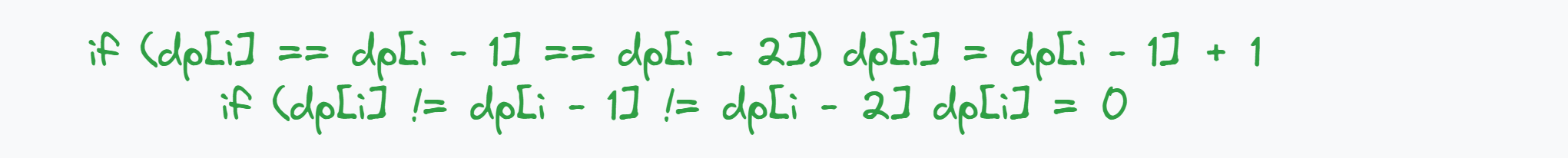
-
初始化
为了防止后续的填表不越界
dp[0] = 0, dp[1] = 0 -
填表
从左到右
-
返回值
dp表的所有元素之和
AC代码:
class Solution
{
public:
int numberOfArithmeticSlices(vector<int>& nums)
{
int n = nums.size();
vector<int> dp(n);
int sum = 0;
for (int i = 2; i < n; i++)
{
if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2])
{
dp[i] = dp[i - 1] + 1;
}
sum += dp[i];
}
return sum;
}
};
6. 最长湍流子数组
题目链接
-
状态表示
f[i] 以 i 位置为结尾的所有子数组当中,最后呈现“上升” 状态下最长湍流子数组的长度g[i] 以 i 位置为结尾的所有子数组当中,最后呈现“下降”状态下最长湍流子数组的长度 -
状态转移方程

-
初始化
表里的数据都初始化为1
-
填表
从左到右
-
返回值
返回两个表的最大值
AC代码:
class Solution
{
public:
int maxTurbulenceSize(vector<int>& arr)
{
int n = arr.size();
vector<int> f(n, 1), g(n, 1);
int ret = 1;
for (int i =1; i < n; i++)
{
if (arr[i] > arr[i - 1]) f[i] = g[i - 1] + 1;
else if (arr[i] < arr[i - 1]) g[i] = f[i - 1] + 1;
ret = max(ret, max(f[i], g[i]));
}
return ret;
}
};
7. 单词拆分
题目链接
-
状态表示
dp[i] 表示0到i之间的字符串能否被字典拼接 -
状态转移方程

-
初始化
可以在字符串s前面加上一个占位符这样就可以没有下标的映射关系
-
填表
从左到右
-
返回值
AC代码:
class Solution
{
public:
bool wordBreak(string s, vector<string>& wordDict)
{
unordered_set<string> hash;
for (auto e : wordDict) hash.insert(e);
int n = s.size();
vector<bool> dp(n + 1);
dp[0] = true;
s = ' ' + s;
for (int i = 1; i <= n; i++)
{
for (int j = i; j >= 1; j--)
{
if (dp[j - 1] && hash.count(s.substr(j, i - j + 1)))
{
dp[i] = true;
break;
}
}
}
return dp[n];
}
};
8. 环形字符串中的唯一的子字符串
题目链接
-
状态表示
dp[i]表示到 i 位置的所有子串当中有多少个在base中出现过 -
状态转移方程

-
初始化
初始化为1
-
填表
-
返回值
由于dp表当中存的值可能是重复的,所以需要进行去重操作。相同字符串结尾的dp值,取最大的值即可
AC代码:
class Solution
{
public:
int findSubstringInWraproundString(string s)
{
int n = s.size();
vector<int> dp(n, 1);
for (int i = 1; i < n; i++)
{
if ((s[i - 1] + 1 == s[i]) || (s[i - 1] == 'z' && s[i] == 'a'))
{
dp[i] = dp[i - 1] + 1;
}
}
int hash[26] = {0};
int sum = 0;
for (int i = 0; i < n; i++)
{
hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);
}
for (auto x : hash) sum += x;
return sum;
}
};