论文题目

SVO: Semidirect Visual Odometry for Monocular and Multicamera Systems

内容

1） 具有最小特征漂移的长特征轨迹；
2） 图像平面中的大量均匀分布的特征；
3）新特征与旧地标的可靠关联（即环路闭合）。

算法不限于使用局部点特征（例如，角或斑点），而是可以跟踪边缘[14]，或者更一般地，跟踪图像中具有梯度的所有像素时，例如，在具有少量或高频纹理的场景（例如，沙子[12]或沥青[13]）中，许多像素被可靠跟踪的概率会增加，例如在密集[15]或半密集方法[16]中。

效率的提高是由于以下三个原因:首先，SVO只提取平行线程中选定关键帧的特征，因此与硬实时约束解耦。其次，所提出的直接跟踪算法消除了鲁棒数据关联的必要性。最后，与以前的直接方法相反，SVO只需要对环境进行稀疏重建

与svo1的提升:1本文的新颖之处在于推广到宽视场（FoV）透镜（见第VII节）、多摄像机系统（见第VIII节）、包含运动先验（见第IX节）和边缘特征的使用。

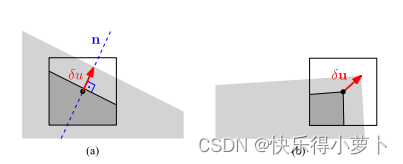
图4。拐角和小边的不同对齐策略。边缘特征的对齐被限制在边缘的法线方向n上。（a） 边缘对齐。（b） 拐角对齐。

Relaxation and Refinement

随着对准中帧之间距离的增加，不能保证对准的鲁棒性（见第XI-A节中的实验）。因此，我们建议放宽由三维点的重投影给出的几何约束，并对相应的特征块执行单独的二维对齐。相对于来自第一次提取特征的帧的参考补丁来执行新帧中的每个补丁的对准；因此，最老的帧是可能的，这应该最大限度地减少特征漂移。然而，二维对齐会产生重投影误差，即投影的三维点和对齐的特征之间的差异。因此，在最后一步中，我们执行束调整，以优化三维点的位置和相机姿态，从而将重新投影误差降至最低。我们特别注意位于强度梯度边缘上的特征。

对齐

对于点的
$$\begin{array}{l}{\mathbf{u}}^{\prime \ast }={\mathbf{u}}^{\prime }+\delta {\mathbf{u}}^{\star },\text{ with }{\mathbf{u}}^{\prime }=\pi \left({\mathrm{T}}_{\mathrm{CB}}{\mathrm{T}}_{kr}{\mathrm{T}}_{\mathrm{BC}}{\pi }_{\rho }^{-1}(\mathbf{u})\right)\\ \delta {\mathbf{u}}^{\star }=\arg {\min }_{\delta \mathbf{u}}{\sum }_{\Delta \mathbf{u}\in \mathcal{P}}\frac{1}{2}{\Vert {\mathrm{I}}_k^{\mathrm{C}}\left({\mathbf{u}}^{\prime }+\delta \mathbf{u}+\Delta \mathbf{u}\right)-{\mathrm{I}}_r^{\mathrm{C}}(\mathbf{u}+\mathbf{A}\Delta \mathbf{u})\Vert }^2\end{array}$$

对于边缘点的(这里的n是梯度方向)
$$\begin{array}{l}{\mathbf{u}}^{\prime \star }={\mathbf{u}}^{\prime }+\delta u^{\star }\cdot \mathbf{n},\text{ with }\\ \delta u^{\star }=\arg {\min }_{\delta u}{\sum }_{\Delta \mathbf{u}\in \mathcal{P}}\frac{1}{2}{\Vert {\mathrm{I}}_k^{\mathrm{C}}\left({\mathbf{u}}^{\prime }+\delta u\cdot \mathbf{n}+\Delta \mathbf{u}\right)-{\mathrm{I}}_r^{\mathrm{C}}(\mathbf{u}+\mathbf{A}\Delta \mathbf{u})\Vert }^2\end{array}$$

优化位姿

在特征对齐之后，我们建立了具有亚像素精度的特征对应关系。然而，特征对齐违反了对极约束，并引入了重投影误差δu，该误差通常远低于0.5像素。因此，在运动估计的最后一步中，我们通过最小化重投影误差的平方和来细化相机姿态和地标位置$X=T_{kW}，\rho i$
$$\begin{array}{rl}{\mathcal{X}}^{\star }=& \arg \underset{\mathcal{X}}{\min }\sum _{k\in \mathcal{K}}\sum _{i\in {\mathcal{L}}_k^C}\frac{1}{2}{\Vert {\mathbf{u}}_i^{\prime \ast }-\pi \left({\mathrm{T}}_{\mathrm{CB}}{\mathrm{T}}_{k\mathrm{W}}{\mathbf{\rho }}_i\right)\Vert }^2\\ & +\sum _{k\in \mathcal{K}}\sum _{i\in {\mathcal{L}}_k^E}\frac{1}{2}{\Vert {\mathbf{n}}_i^{\top }\left({\mathbf{u}}_i^{\prime \ast }-\pi \left({\mathrm{T}}_{\mathrm{CB}}{\mathrm{T}}_{k\mathrm{W}}{\mathbf{\rho }}_i\right)\right)\Vert }^2\end{array}$$

大fov相机

为了估计新特征的深度（参见第六节），我们需要沿着核线对像素进行采样。对于失真的图像，极线是弯曲的（见图7）。因此，我们定期对大圆进行采样，大圆是对极平面与以感兴趣的相机姿态为中心的单位球体的交点。采样的角度分辨率大约对应于图像平面中的一个像素。对于每个样本，我们应用相机投影模型π（·）来获得弯曲核线上对应的像素坐标。

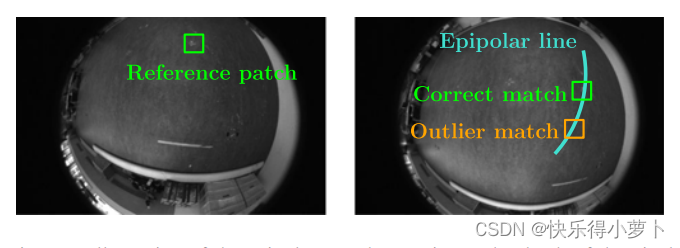
用于估计左图像中参考补丁中心像素深度的极线搜索示意图。给定两个图像的外在和内在校准，计算对应于参考像素的核线。由于自相似的纹理，沿着极线的错误匹配是经常发生的。

多相机系统

所提出的运动估计算法从相对姿态Tk k−1的优化开始。由于在第V-A节中，我们已经介绍了一个固定在相机上的机身框架B，因此现在可以直接将稀疏图像对齐推广到多个相机。给定具有M个相机的相机装备（见图9），我们假设单个相机c∈c相对于机身$T_{CB}$的相对姿态是从外部校准中已知的。3为了将稀疏图像对准推广到多个相机，我们只需要在（1）的成本函数中添加一个额外的代价函数
$${\mathrm{T}}_{kk-1}^{\star }=\arg \underset{{\mathrm{T}}_{k-1}}{\min }\sum _{\mathrm{C}\in \mathrm{C}}\sum _{\mathbf{u}\in {\overline{\mathcal{R}}}_{k-1}^{\mathrm{C}}}\frac{1}{2}{\Vert {\mathbf{r}}_{{\mathrm{I}}_{\mathrm{u}}^{\mathrm{C}}}\left({\mathrm{T}}_{kk-1}\right)\Vert }_{{\Sigma }_{\mathrm{I}}}^2.$$

运动先验

在特征较差的环境中，在快速运动过程中，或在动态障碍物的情况下，使用运动先验可能非常有帮助。运动先验是在（11）中添加到成本函数的附加项，它惩罚与先验估计不一致的运动。因此，可以抑制由于无约束DoF或异常值引起的运动估计中的“跳跃”。例如，在汽车场景中，可以假设等速运动模型，因为汽车的惯性阻止了从一帧到下一帧的突然变化。其他先验可能来自额外的传感器，如陀螺仪，这使我们能够测量两帧之间的增量旋转。
假设我们在$p_{k,k-1}$之前得到了相对平移（例如，来自恒定速度假设），在$R_{k,k-1}$之后得到了相对旋转（例如，源自积分陀螺仪）。在这种情况下，我们可以通过向稀疏图像对齐步骤的成本添加附加项来使用运动先验

$$\begin{array}{rl}{\mathrm{T}}_{kk-1}^{\star }=& \arg \underset{{\mathrm{T}}_{kk-1}}{\min }\sum _{\mathbf{c}\in \mathrm{C}}\sum _{\mathbf{u}\in {\overline{\mathcal{R}}}_{k-1}^{\mathrm{c}}}\frac{1}{2}{\Vert {\mathbf{r}}_{{\mathrm{I}}_{\mathbf{u}}^{\mathrm{C}}}\left({\mathrm{T}}_{kk-1}\right)\Vert }_{{\Sigma }_{\mathrm{I}}}^2\\ & +\frac{1}{2}{\Vert {\mathbf{p}}_{kk-1}-{\tilde{\mathbf{p}}}_{kk-1}\Vert }_{{\Sigma }_{\mathbf{p}}}^2\\ & +\frac{1}{2}{\Vert \log {\left({\tilde{\mathrm{R}}}_{kk-1}^{\top }{\mathrm{R}}_{kk-1}\right)}^{\vee }\Vert }_{{\Sigma }_{\mathrm{R}}}^2\end{array}$$

实现细节

在本节中，我们将提供有关我们实施的各个方面的更多详细信息。

Initialization

该算法使用[58]中的五点相对姿态算法进行自举，以获得前两个关键帧的姿态和初始贴图。在多摄像机配置中，通过立体匹配来获得初始映射。

Sparse Image Alignment

对于稀疏图像对齐，我们使用4×4像素的补丁大小。在实验部分，我们证明了具有如此小的补丁大小的稀疏方法实现了可比性当帧间距离很小时，在鲁棒性方面优于半密集和密集方法，这对于帧到帧的运动估计来说通常是正确的。为了处理大的运动，我们以粗到细的方案应用稀疏图像对齐算法。因此，对图像进行半采样以创建五个级别的图像金字塔。然后，从初始条件$T_{k,k-1}=I_{4\times 4}$开始，在最粗略的水平上优化光度成本，直到收敛。随后，在下一个更精细的级别上继续优化，以提高结果的精度。为了节省处理时间，我们在第三级收敛后停止，在这个阶段，估计足够准确，可以初始化特征对齐。为了提高对动态障碍、遮挡和反射的鲁棒性，我们还采用了鲁棒成本函数[24]，[34]。

Feature Alignment

对于特征对齐，我们使用8×8像素的补丁大小。由于参考补丁可能是多帧旧的，我们使用仿射照明模型来应对照明变化[59]。对于所有实验，我们将匹配特征的数量限制为180，以保证每帧的成本不变。

Mapping

在映射线程中，我们将图像划分为固定大小的单元（例如，32×32像素）。对于每个关键帧，在单元中得分最高的FAST角[60]处初始化一个新的深度过滤器，除非已经存在2-D到3-D的对应关系。在没有发现角的单元中，我们检测具有最高梯度大小的像素，并初始化边缘特征。这将在图像中产生均匀分布的特征。为了加快深度估计，我们只对沿极线的短距离进行采样；在我们的情况下，该范围对应于当前深度估计的标准偏差的两倍。我们使用8×8像素的补丁大小进行核极搜索。

总结

在本文中，我们提出了半直接VO算法“SVO”，它比当前最先进的VO算法快得多，同时实现了极具竞争力的精度。速度的提高是由于只为并行线程中选定的关键帧提取特征，并且使用新的稀疏图像对齐算法可以非常快速和稳健地建立特征匹配。稀疏图像对齐在极线约束下联合跟踪一组特征，当特征位置的场景深度已知时，可以使用稀疏图像对齐来代替KLT跟踪[69]。我们进一步建议使用明确建模异常值测量的鲁棒滤波器来估计场景深度。稳健的深度估计和直接跟踪使我们能够跟踪非常弱的拐角特征和边缘。SVO的另一个好处是，它直接从优化开始，这使我们能够轻松地集成来自多个相机的测量以及运动先验。公式可进一步在配有鱼眼和折反射透镜的大型FoV相机使用。SVO算法已被进一步证明在现实世界的应用中是成功的，例如基于视觉的四旋翼飞行[54]或智能手机的三维扫描应用。