Q1：6917. 满足目标工作时长的员工数目（简单枚举模拟题）

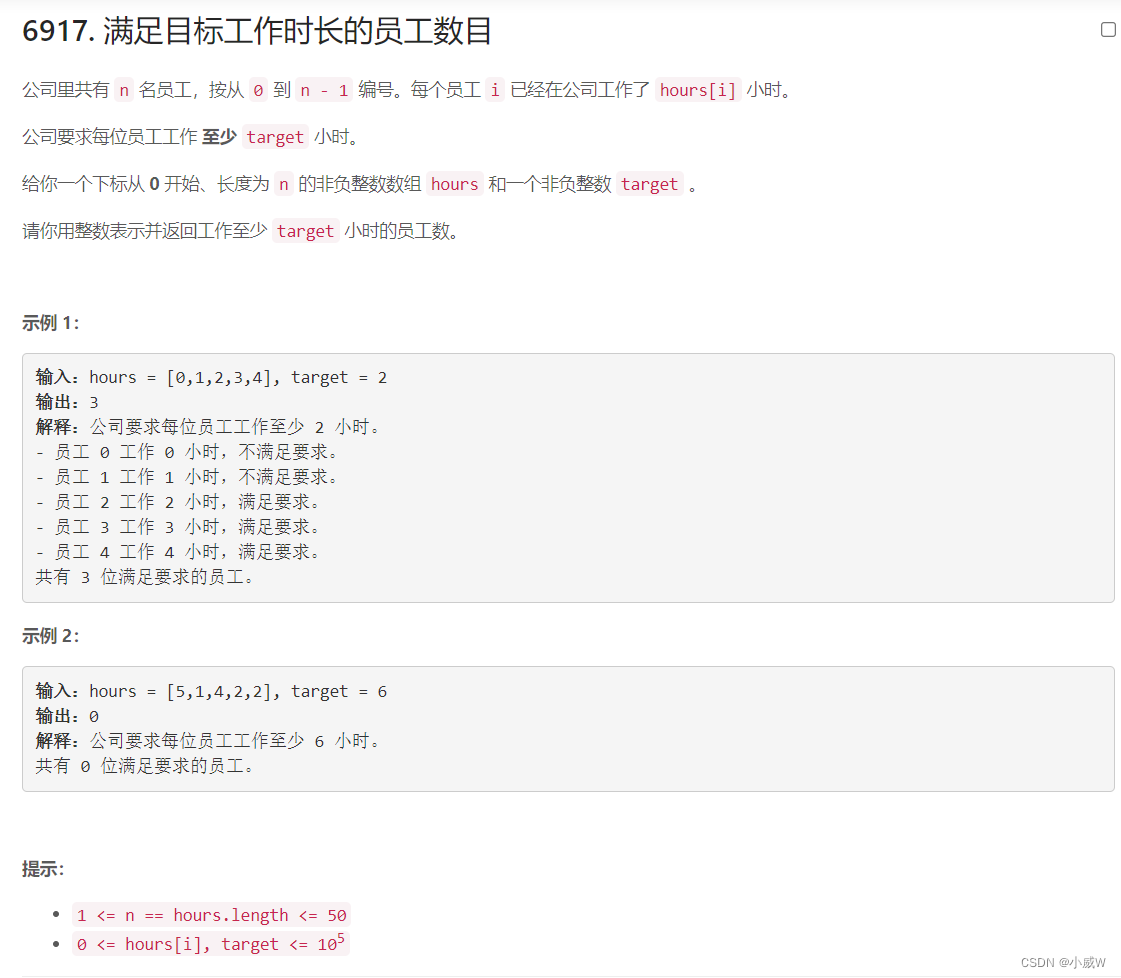
在这里插入图片描述

按题意枚举遍历一遍即可。

class Solution {
    public int numberOfEmployeesWhoMetTarget(int[] hours, int target) {
        int ans = 0;
        for (int h: hours) {
            if (h >= target) ans++;
        }
        return ans;
    }
}

Q2：6900. 统计完全子数组的数目（双指针+滑动窗口）

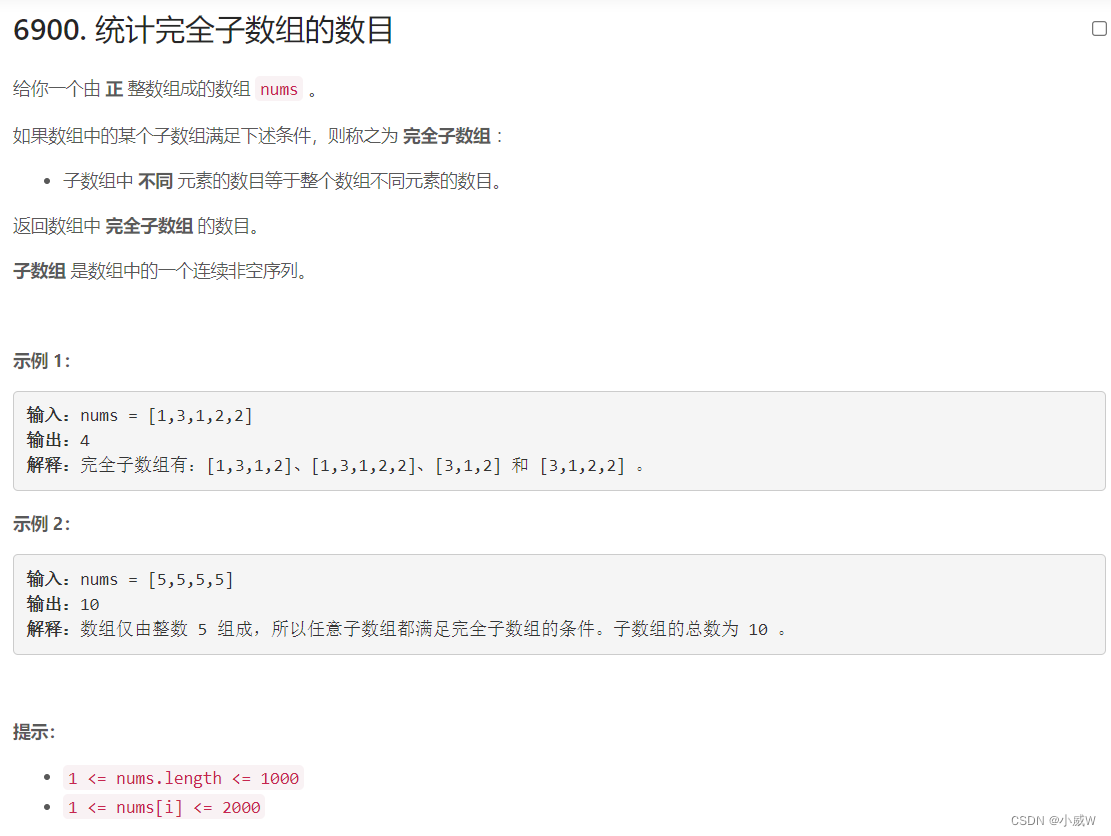
在这里插入图片描述

数据范围比较小只有1000，使用 $O(n^2)$ 的方法估计也能过，但是这里我使用了 $O (n)$ 的双指针 + 滑动窗口。

枚举的是右端点，不断尝试将左端点向右移动。
对于每个右端点，当前左指针向左的所有位置都可以作为左端点，所以 ans += l + 1。

class Solution {
    public int countCompleteSubarrays(int[] nums) {
        Set<Integer> s = new HashSet();
        for (int num: nums) s.add(num);
        
        int n = nums.length, sum = s.size(), ans = 0;
        Map<Integer, Integer> m = new HashMap();
        for (int r = 0, l = 0; r < n; ++r) {
            m.merge(nums[r], 1, Integer::sum);
            while (m.get(nums[l]) > 1) {
                m.merge(nums[l], -1, Integer::sum);
                l++;
            }
            if (m.size() == sum) ans += l + 1;
        }
        return ans;
    }
}

Q3：6918. 包含三个字符串的最短字符串

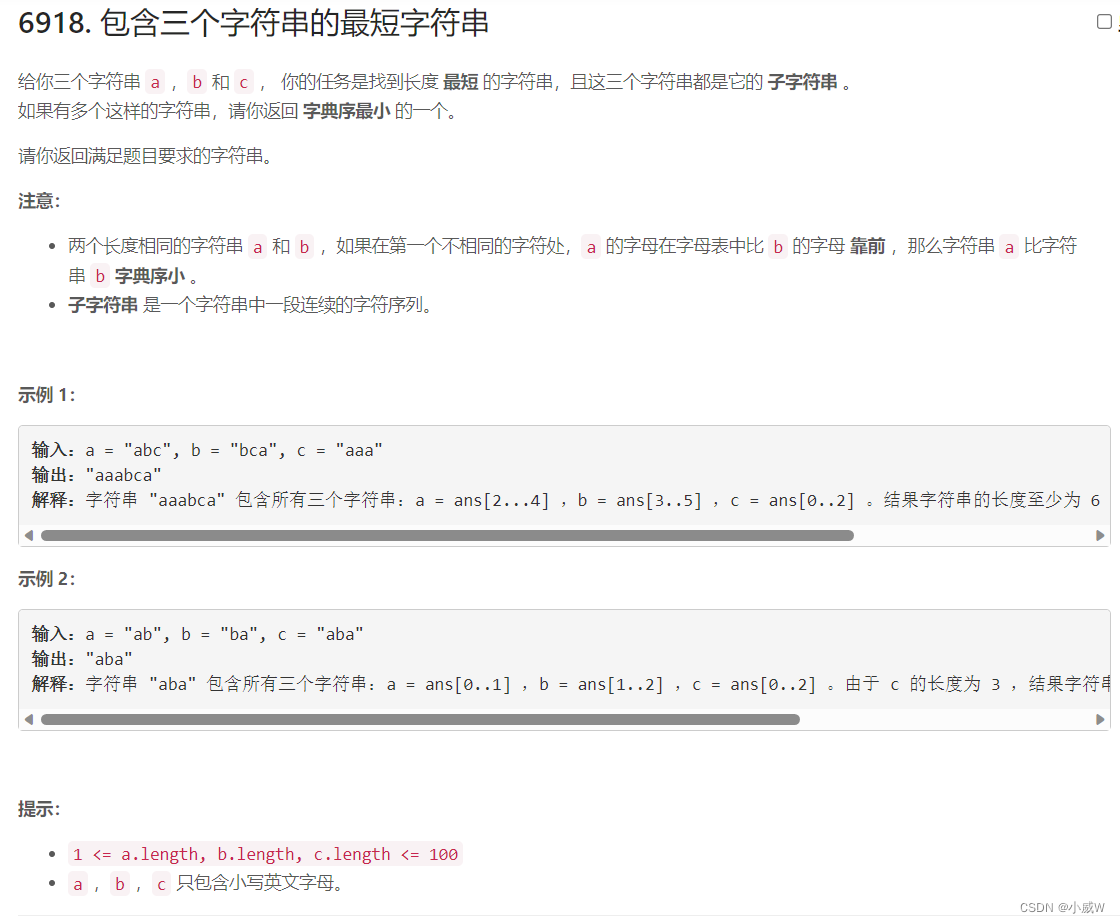
在这里插入图片描述

这题感觉是挺怪的，但是数据范围比较小，字符串的长度只有 100 ，而且只有 3 个字符串。

只有 3 个字符串意味着只有 6 种拼接可能，分别是 abc，acb，bac，bca，cab，cba。（拼接的原则是找到最长的公共前后缀）
将这 6 个字符串放入列表中，按照长度 + 字典序排序即可。

class Solution {
    public String minimumString(String a, String b, String c) {
        List<String> ls = new ArrayList();
        ls.add(op(a, b, c));
        ls.add(op(a, c, b));
        ls.add(op(b, a, c));
        ls.add(op(b, c, a));
        ls.add(op(c, a, b));
        ls.add(op(c, b, a));
        Collections.sort(ls);
        int l = ls.get(0).length(), id = 0;
        for (int i = 1; i < 6; ++i) {
            if (ls.get(i).length() < l) {
                l = ls.get(i).length();
                id = i;
            }
        }
        return ls.get(id);
    }
    
    public String op(String a, String b, String c) {
        String ans = new String(op2(op2(a, b), c));
        return ans;
    }
    
    public String op2(String a, String b) {
        for (int i = 0; i < b.length(); ++i) {
            String t = a + b.substring(b.length() - i, b.length());
            if (t.indexOf(b) != -1) return new String(t);
        }
        return new String(a + b);
    }
}

Q4：6957. 统计范围内的步进数字数目（数位DP）

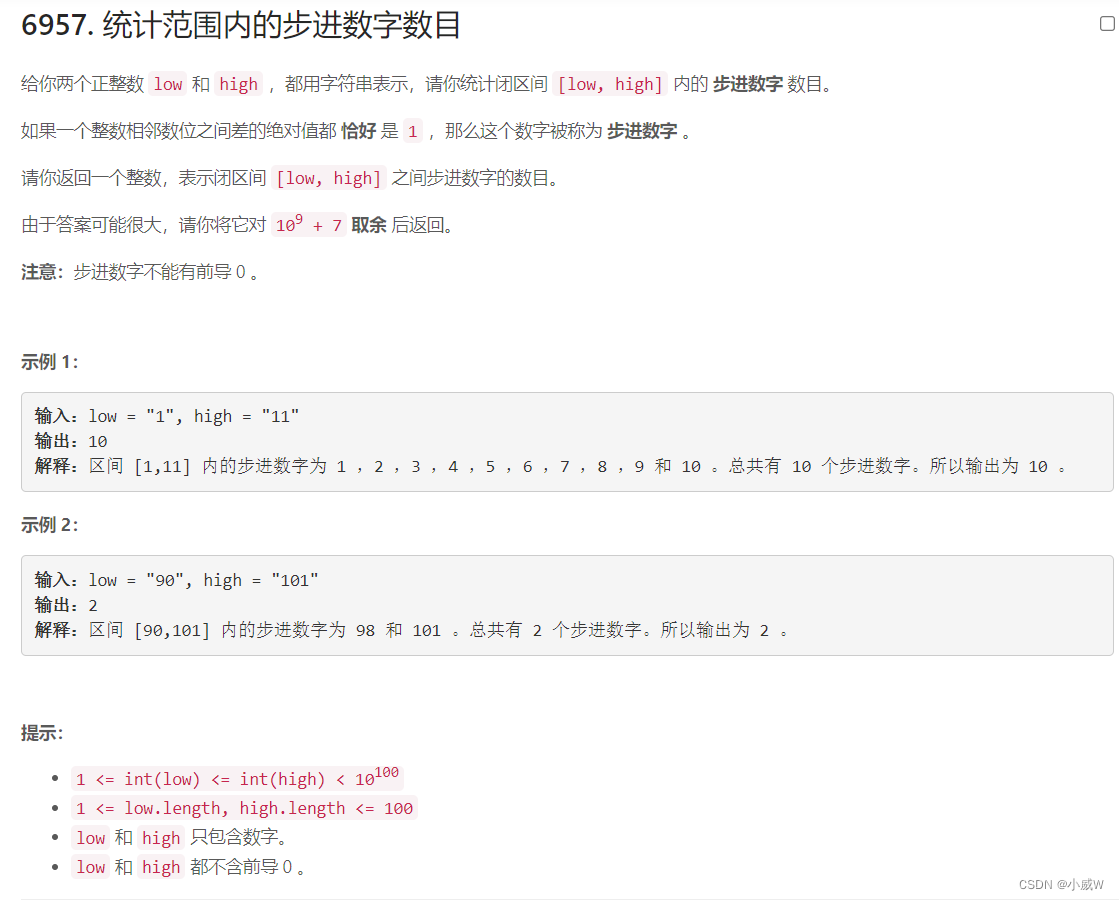
在这里插入图片描述

经典的数位DP题目，相关的链接可见：
【算法】数位DP
【算法基础：动态规划】5.4 数位统计DP（计数问题）（数位DP）

class Solution {
    char[] s;
    int[][] memo;
    final int mod = (int)1e9 + 7;
    
    public int countSteppingNumbers(String low, String high) {
        int ans = op(high) - op(low);
        if (check(low)) ans++;
        return (ans + mod) % mod;		// 不要忘了取模
    }
    
    public int op(String n) {
        s = n.toCharArray();
        int m = s.length;
        memo = new int[m][10];
        for (int i = 0; i < m; ++i) Arrays.fill(memo[i], -1);
        return f(0, true, false, -1);
    }
    
    public int f(int i, boolean isLimit, boolean isNum, int last) {
        if (i == s.length) return isNum? 1: 0;
        if (!isLimit && isNum && memo[i][last] != -1) return memo[i][last];
        
        int res = 0;
        if (!isNum) res = f(i + 1, false, false, -1) % mod;
        
        int up = isLimit? s[i] - '0': 9;
        for (int d = isNum? 0: 1; d <= up; ++d) {
            if (Math.abs(d - last) == 1 || last == -1) res = (res + f(i + 1, isLimit && d == up, true, d)) % mod;
        }
        if (!isLimit && isNum) memo[i][last] = res;
        return res;
    }
    
    // 单独检查 low 是不是步进数字
    public boolean check(String s) {
        char ch = s.charAt(0);
        for (int i = 1; i < s.length(); ++i) {
            char ch2 = s.charAt(i);
            if (ch == ch2 + 1 || ch == ch2 - 1) ch = ch2;
            else return false;
        }
        return true;
    }
}