骑士的最短路径 II :

在 国际象棋 中 , 骑士 类似 与 象棋 中的 马 , 走 " 日 " 字 格子 ;

骑士有 8 种走法 : " 日 " 字 格子 , 参考 百度百科

• 左走一格向前走两格
• 左走一格向后走两格
• 左走两格向前走一格
• 左走两格向后走一格
• 右走一格向前走两格
• 右走一格向后走两格
• 右走两格向前走一格
• 右走两格向后走一格

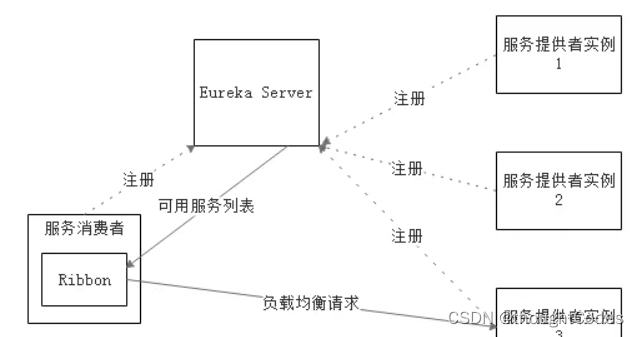
下图是 骑士 的走法 , 黑色是 骑士的初始位置 ( 0 , 0 ) , 绿色 和 红色 是 骑士 可以走的 下一步位置 ;

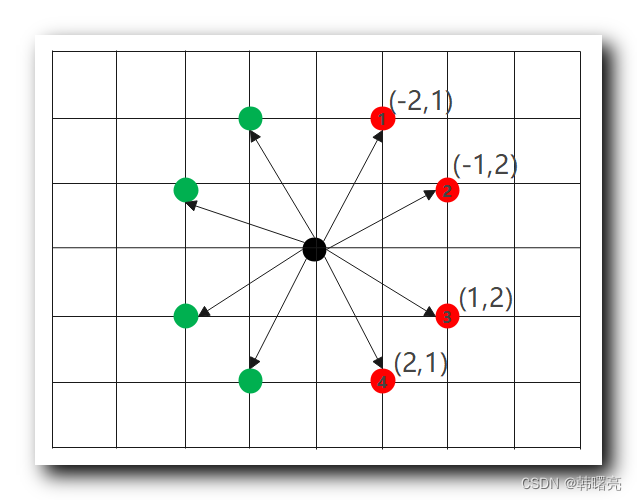
给定一个二维坐标 , 在该坐标系中 , 骑士只能走 上图中 右边 红色的四个方向的步骤 , 计算从 左上角 到 右下角 的最短路径数 ;

一、问题分析

---

如果 骑士 可以走 8 个方向 ,

• 那么需要 使用 BFS 宽度优先搜索 算法 ;
• 此时 不能使用 动态规划解决上述问题 , 如果 可以走 8 个方向 , 那么路径就可以反复 , 会出现 循环依赖的情况 ;

如果 骑士 只能走右边的 4 个方向 , 没有循环依赖 , 则可以使用动态规划 , 解决上述问题 ;

如果 骑士 只能走 右侧的 四个方向 , 也就是

• 从 黑点 走到 红点 1 , 纵坐标方向上 i 减少 2 行 , 横坐标方向上 j 增加 1 列 ;
• 从 黑点 走到 红点 2 , 纵坐标方向上 i 减少 1 行 , 横坐标方向上 j 增加 2 列 ;
• 从 黑点 走到 红点 3 , 纵坐标方向上 i 增加 1 行 , 横坐标方向上 j 增加 2 列 ;
• 从 黑点 走到 红点 4 , 纵坐标方向上 i 增加 2 行 , 横坐标方向上 j 增加 1 列 ;

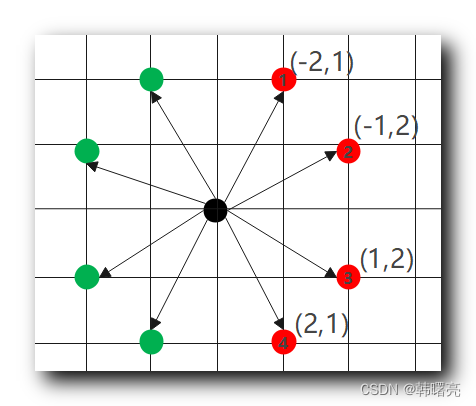
那么 如果当前位置是 ( i , j ) , 那么当前位置的 最短路径 是 dp[i][j] , 那么该点的 最短路径 依赖于 如下几个点的最短路径 :

• ( i + 2 , j - 1 ) , 对应 从 黑点 走到 红点 1 , 纵坐标方向上 i 减少 2 行 , 横坐标方向上 j 增加 1 列 ;
• ( i + 1 , j - 2 ) , 对应 从 黑点 走到 红点 2 , 纵坐标方向上 i 减少 1 行 , 横坐标方向上 j 增加 2 列 ;
• ( i - 1 , j - 2 ) , 对应 从 黑点 走到 红点 3 , 纵坐标方向上 i 增加 1 行 , 横坐标方向上 j 增加 2 列 ;
• ( i - 2 , j - 1 ) , 对应 从 黑点 走到 红点 4 , 纵坐标方向上 i 增加 2 行 , 横坐标方向上 j 增加 1 列 ;

初始化状态值时 , dp[i][j] 代表了从 起始点 ( 0 , 0 ) 位置 跳转到 ( i , j ) 位置的 最短路径数 ;

该算法求的是 最短路径数 , 初始化 状态 值 时 , 不能初始化为 0 , 这里 初始化为 Integer.MAX_VALUE 值 , 如果值为 Integer.MAX_VALUE 说明该点走不到 ;

如果 算法求的是 方案数 , 则初始化状态值时 , 可以初始化为 0 ;

二、代码示例

---

代码示例 :

class Solution {

    // 根据骑士只能向右的四个方向 , 走到 (i, j) 点的最短路径, 需要依赖
    // ( i + 2 , j - 1 )
    // ( i + 1 , j - 2 )
    // ( i - 1 , j - 2 )
    // ( i - 2 , j - 1 )
    // 四个点的最短路径, 将上述累加值保存到数组中, 用于快速找到依赖点
    public static int[] deltaX = {2, 1, -1, -2};
    public static int[] deltaY = {-1, -2, -2, -1};

    public int shortestPath2(int[][] obstacleGrid) {
        // 验证函数参数
        if (obstacleGrid == null || obstacleGrid.length == 0) {
            return 0;
        }

        // 1. 动态规划状态 State
        // dp[i][j] 表示 从 (0, 0) 位置出发 , 到 (i, j) 位置的方案总数 ;
        int m = obstacleGrid.length, n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];

        // 2. 动态规划初始化 Initialize
        // 还没开始跳, 此时先将所有的点的状态值设置为 Integer.MAX_VALUE
        // 含义是 所有的点 都无法跳到 , 需要跳无数次才能跳到
        // 但是 (0, 0) 点除外, 其本身跳到本身路径数为 0
        for (int i = 0; i < m ; i++) {
            for (int j = 0; j < n; j++) {
                dp[i][j] = Integer.MAX_VALUE;
            }
        }
        dp[0][0] = 0;

        // 3. 动态规划方程 Function
        // 运动时 , 只能向 右侧的 四个日字方向走
        // ① 纵坐标方向上 i 减少 2 行 , 横坐标方向上 j 增加 1 列 ;
        // ② 纵坐标方向上 i 减少 1 行 , 横坐标方向上 j 增加 2 列 ;
        // ③ 纵坐标方向上 i 增加 1 行 , 横坐标方向上 j 增加 2 列 ;
        // ④ 纵坐标方向上 i 增加 2 行 , 横坐标方向上 j 增加 1 列 ;
        // 从这四个方向中 , 找出路径最小的方向即可
        // 如果遇到障碍物 , 则需要 continue 跳过本次计算 , 继续执行下一次计算 ;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 遇到障碍物 , 跳过
                if (obstacleGrid[i][j] == 1) {
                    continue;
                }

                // 遍历依赖的四个方向
                for (int d = 0; d < 4; d++) {
                    int x = i + deltaX[d];
                    int y = j + deltaY[d];

                    // 判断 x, y 是否超出边界
                    if (x < 0 || x >= n || y < 0 || y >= m) {
                        continue;
                    }

                    // 判断当前位置是否可达, 如果为无穷大 , 说明不可达
                    if (dp[x][y] == Integer.MAX_VALUE) {
                        continue;
                    }

                    // 取当前依赖路径的最小值作为最终的 最小路径数
                    dp[i][j] = Math.min(dp[i][j], dp[x][y] + 1);
                }
            }
        }

        // 4. 动态规划答案 Answer
        if (dp[m - 1][n - 1] == Integer.MAX_VALUE) {
            System.out.println("终点不可达");
            return -1;
        }
        return dp[m - 1][n - 1];
    }

    public static void main(String[] args) {
        // 1 的位置是障碍物
        int[][] obstacleGrid = {{0,0,0,0}, {0,0,0,0}, {0,0,0,0}, {0,0,0,0}};
        int result = new Solution().shortestPath2(obstacleGrid);
        System.out.println("最短路径数为 " + result);
    }
}

执行结果 :

最短路径数为 2