最近学习数据结构,对于从未接触过数据结构的我来说,老师不仅讲解理论,还有代码的逐层分析,非常不错,受益匪浅!!!(以下是学习记录)
数据结构与算法(Python语言描述)——完整顺序版_哔哩哔哩_bilibili
目录
1.重点+基础语法
2.时间复杂度(主要关注最坏时间复杂度)
3.timeit,list,dic内置函数
4.数据结构
5.顺序表
5.1 顺序表的2个形式
5.2 顺序表的结构与实现
5.3 顺序表数据区扩充
5.4 顺序表的操作
5.5 python_list使用顺序表数据结构
6.链表
6.1 链表概念
6.2 单链表的实现
6.3 链表与顺序表的对比
6.4 双向链表
6.5 单向循环链表
7.栈
8.队列
9.排序
1.重点+基础语法
- python语言只要是给出的变量名,里边存储的都是地址值(可以把类,函数,付给变量a)。
如a=5 a=“s” a=Person() a=f 方法。
- time.time()
2.时间复杂度(主要关注最坏时间复杂度)

不同方法间的复杂度
import time
start= time.time()
for i in range(0,1001):
for j in range(0,1001):
for k in range(0,1001):
if i+j+k==1000 and i**2+j**2==k**2:
print(i,j,k)
end = time.time()
print("总开销:",end-start)#总开销: 126.49699997901917
start1= time.time()
for i in range(0,1001):
for j in range(0,1001):
k=1000-i-j
if i**2+j**2==k**2:
print(i,j,k)
end1= time.time()
print("总开销:",end1-start1)#总开销: 1.0120000839233398
- T(n)时间复杂度,n执行的步数
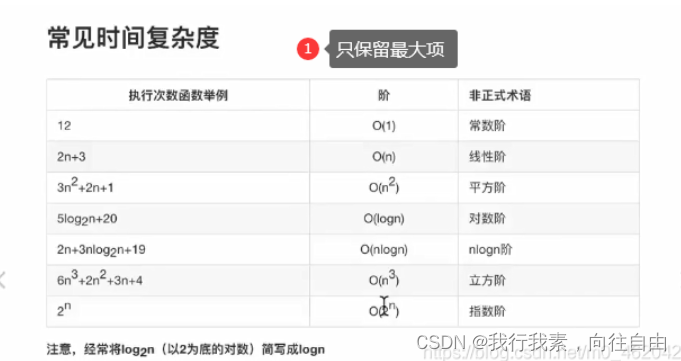
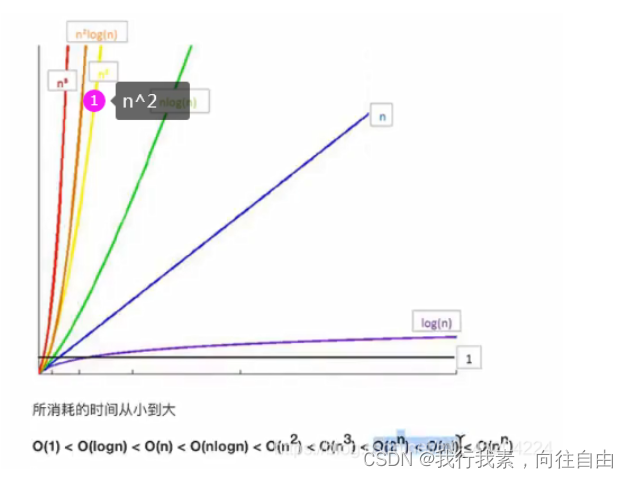
大O表示法,只记录最显著特征O(n)=nxn
- 最坏时间复杂度(平常说的就是这个)
比如对一个list排序,无序的复杂度要高于有序。
基本步骤:顺序,条件(取T最大值),循环
li.append()不能看成一步,只有分析函数中的封装才能看到append的时间复杂度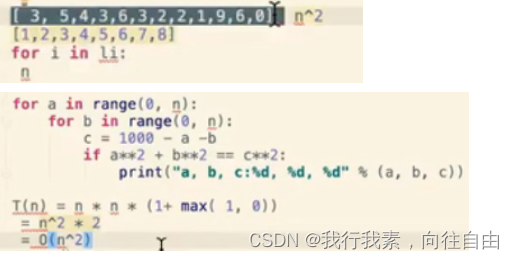
3.timeit,list,dic内置函数
timeit模块

from timeit import Timer
def test():
l=[i for i in range(1000)]
t=Timer("test()","from __main__ import test")##1函数名,2import,因为这个Timer不一定在这里运行
print(t.timeit(number=10000))
对于上例使用不同方法实现时:
1.
('list(range(1000)) ', 0.014147043228149414, 'seconds')
('l = [i for i in range(1000)]', 0.05671119689941406, 'seconds')
('li.append ', 0.13796091079711914, 'seconds')
('concat加 ', 1.7890608310699463, 'seconds')
2.由于数据的存储方式不同,导致插头部和尾部
append()#2.159s
insert(0,i)#30.00s
pop(end)#0.00023,对尾部弹出
pop(0)#1.91


4.数据结构
数据是一个抽象的概念,将其分类后得到程序语言的基本类型,如int,float,char。数据结构指对数据的一种封装组成,如高级数据结构list,字典。数据结构就是一个类的概念,数据结构有顺序表、链表、栈、队列、树。
算法复杂度只考虑的是运行的步骤,数据结构要与数据打交道。数据保存的方式不同决定了算法复杂度。
程序 = 数据结构 + 算法
总结:算法是为了解决实际问题而设计的,数据结构是算法需要处理的问题载体
抽象数据类型(Abstract Data Type):是指一个数学模型以及定义在此数学模型上的一组操作。
class Stu(object):
def adds(self):pass
def pop(self):pass
def sort(self):pass
def modify(self):pass
== 代码编写注意==
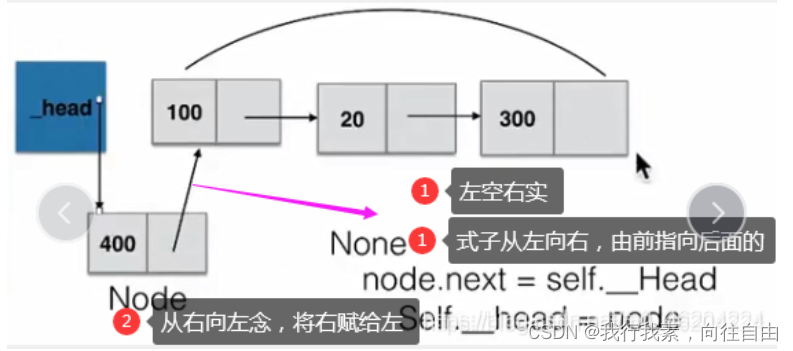
2.对于链表要先接入新的node,再打断原来的,要注意顺序
下面讲的各种表都是一种数据的封装结构
5.顺序表
顺序表+链表=线性表:一根线串起来,两种表都是用来存数据的
5.1 顺序表的2个形式
- 计算机存储
计算机最小寻址单位是1字节,就是一个字节,才有一个地址,所有的地址都是统一大小0x27 4个字节。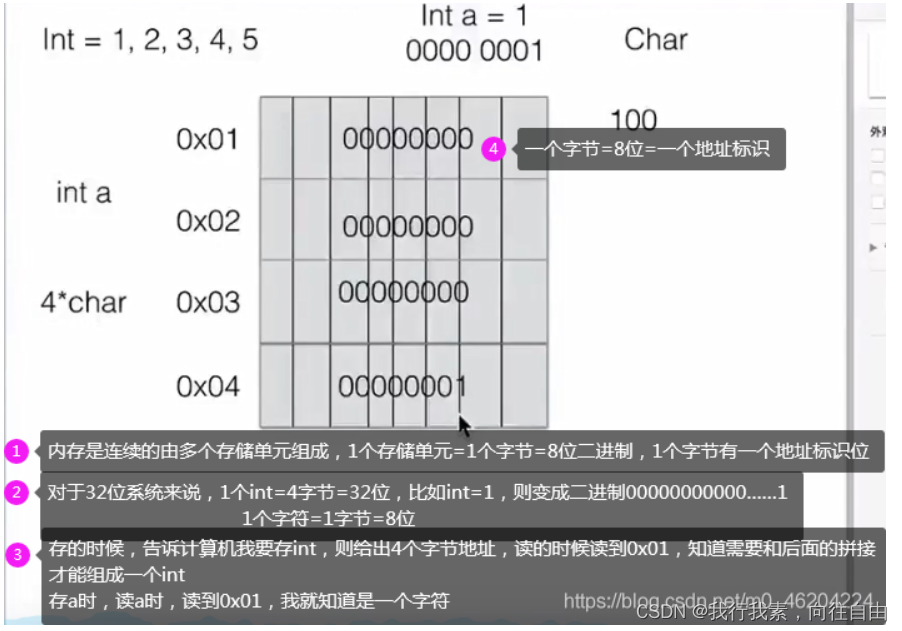
- 元素内置顺序表
对于存放一个含有相同类型元素的list来讲,用顺序表封装成一个数据结构。
- 元素外置顺序表
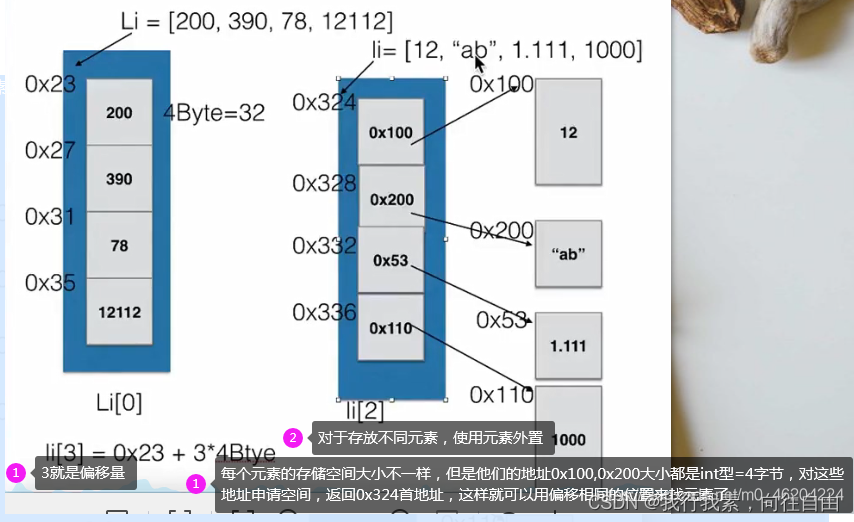
元素内置顺序表,是指存储的数据类型都是一样,这样为每个元素开辟的空间都是一样大的,在根据index找元素的时候
如list1=[1,2,3], 可以根据list的首地址0x12,很容易计算要查询元素的物理地址=0x12+index x 4.
元素外置, 指存的数据类型不一样,如list2=[1,3,“b”,4,“ccc”]

5.2 顺序表的结构与实现
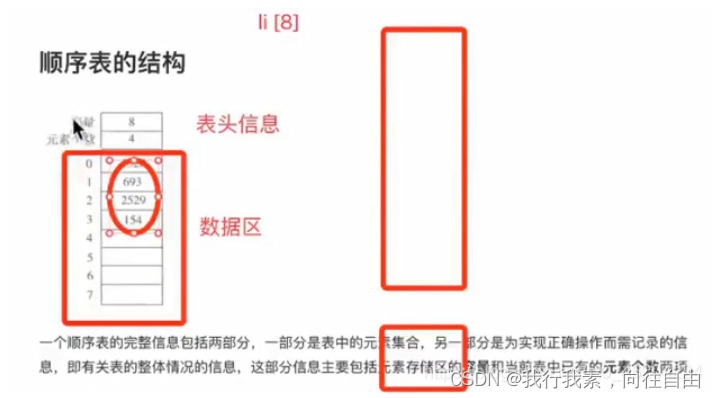
对于python来讲已经做好封装,不需要写容量,元素个数。

元素存储区替换
- 一体式结构由于顺序表信息区与数据区连续存储在一起,所以若想更换数据区,则只能整体搬迁,即整个顺序表对象(指存储顺序表的结构信息的区域)改变了。
- 分离式结构若想更换数据区,只需将表信息区中的数据区链接地址更新即可,而该顺序表对象不变。
- so常用的是分离式
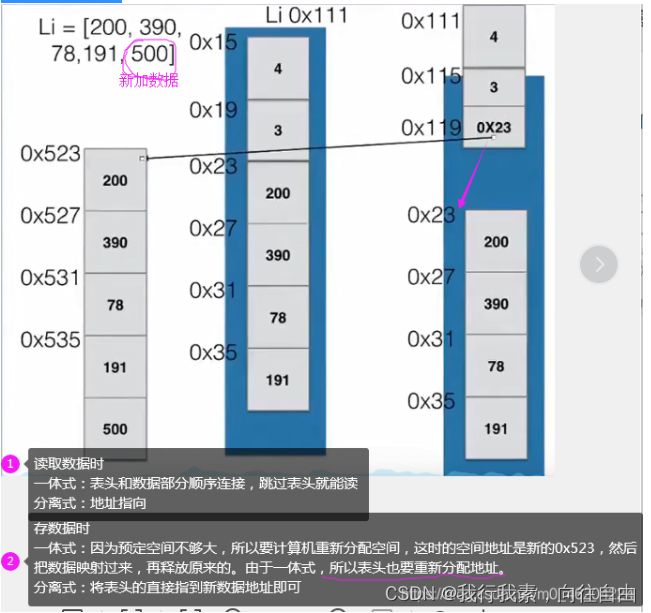
5.3 顺序表数据区扩充
如果数据要来回增,删,导致空间不稳定,所以有了策略:

5.4 顺序表的操作

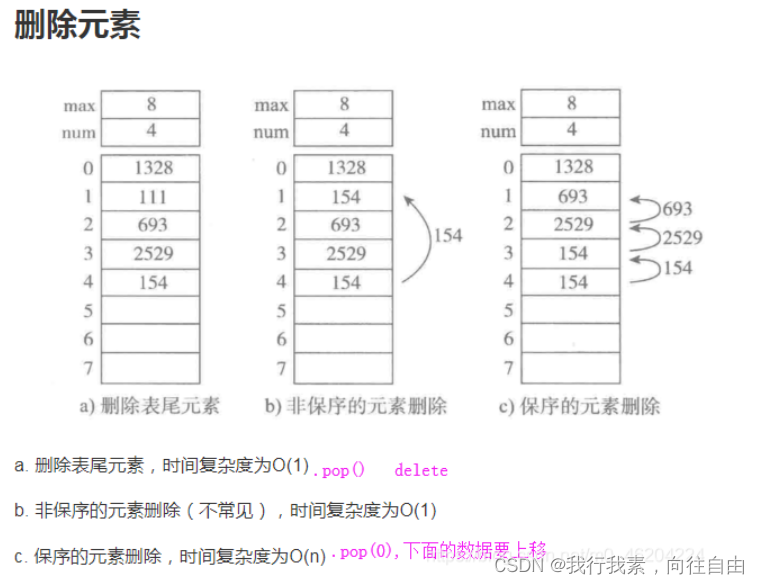
5.5 python_list使用顺序表数据结构
- 表头与数据分离式
- 因为一个list中有int,也有字符所以用的是元素外置
- 动态顺序中的倍数扩充

6.链表
6.1 链表概念
# cur做判断,逻辑(不是指针)走到最后一个元素时,里面的方法体是执行的
# 用cur.next做判断,while循环中是不执行的
# 如果发现少一次执行语句,可以手动打印,就不用完全在while循环中执行

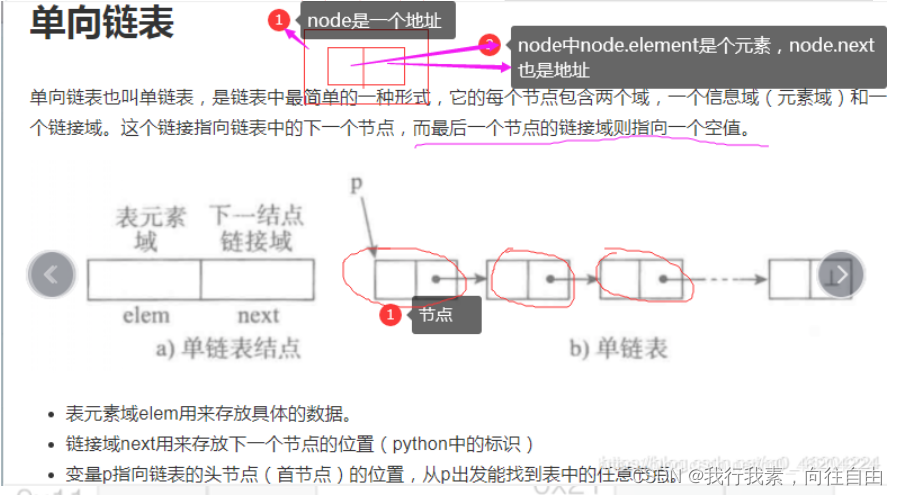
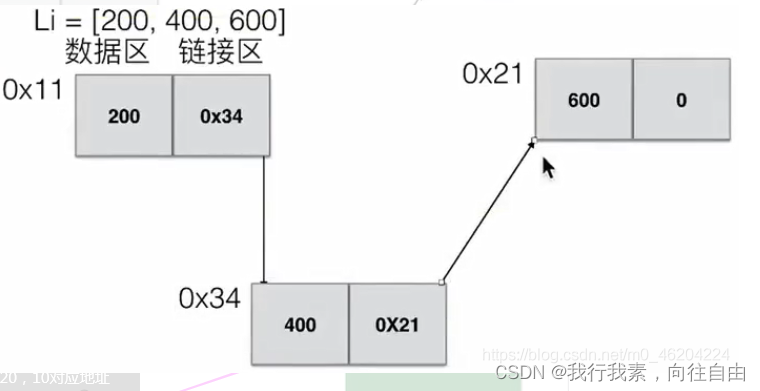
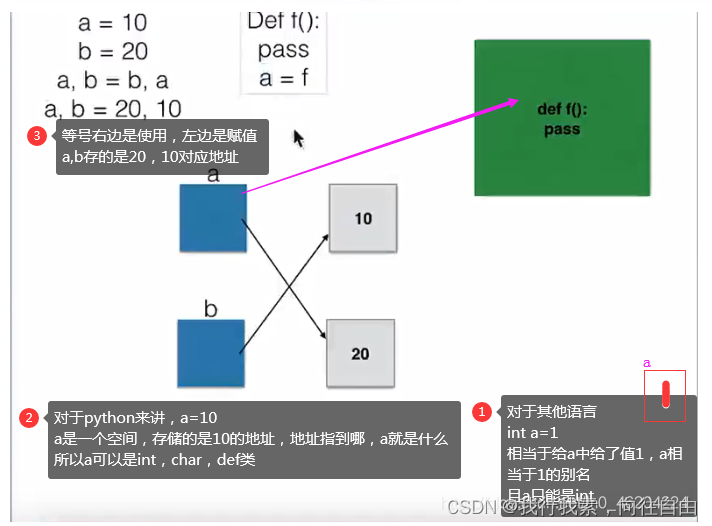
java,c语言是需要中间变量temp,才能完成交换,只有python可以直接交换。
6.2 单链表的实现
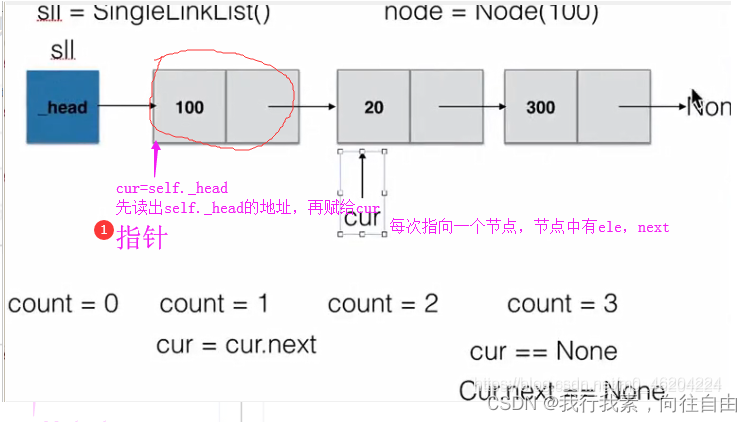
- cur:指针地址
- cur.elment:地址中的元素
- cur=self._head先提出等式右边地址,再给cur
多写几次单链表,有助理解,链表的运行过程。
##1.单链表的节点,里面存放element区和next==>相当于元组(element,next)
class SingleNode(object):
def __init__(self,item):
##item存放数据元素
self.item=item
##next是下一个节点的标识
self.next=None
##2.单链表数据结构类,具有以下功能==>相当于python中的list数据结构类,同时它页具有以下功能
class SingleLinkList(object):
def __init__(self):
self._head=None#私有属性,head=None,说明p指向的单链表中没有node
def is_empty(self):
return self._head==None
def length(self):
cur=self._head
count=0
while cur!=None:
count+=1
cur=cur.next
return count
def travel(self):
##遍历链表
cur=self._head
while cur!=None:
print(cur.item)
cur=cur.next
print("")
def add(self,item):
##头部添加元素
node=SingleNode(item)
node.next=self._head
self._head=node
def append(self,item):
##尾部添加元素
node=SingleNode(item)
if self.is_empty():
self._head=node
else:
cur=self._head
while cur.next!=None:
cur=cur.next
cur.next=node
if __name__=="__main__":
li=SingleLinkList()
print(li.is_empty())
print(li.length())
node=SingleNode(3)
li.append(111)
li.travel()指定位置添加元素:
def insert(self, pos, item):
"""指定位置添加元素"""
# 若指定位置pos为第一个元素之前,则执行头部插入
if pos <= 0:
self.add(item)
# 若指定位置超过链表尾部,则执行尾部插入
elif pos > (self.length()-1):
self.append(item)
# 找到指定位置
else:
node = SingleNode(item)
count = 0
# pre用来指向指定位置pos的前一个位置pos-1,初始从头节点开始移动到指定位置
pre = self._head
while count < (pos-1):
count += 1
pre = pre.next
# 先将新节点node的next指向插入位置的节点
node.next = pre.next
# 将插入位置的前一个节点的next指向新节点
pre.next = node
查找节点是否存在:
def search(self,item):
"""链表查找节点是否存在,并返回True或者False"""
cur = self._head
while cur != None:#一直往后走,起到遇到none停止
if cur.item == item:
return True
cur = cur.next
return False
删除节点:
def remove(self,item):
"""删除节点"""
cur = self._head
pre = None
while cur != None:
# 找到了指定元素
if cur.item == item:
# 如果第一个就是删除的节点
if not pre:
# 将头指针指向头节点的后一个节点
self._head = cur.next
else:
# 将删除位置前一个节点的next指向删除位置的后一个节点
pre.next = cur.next
break
else:
# 继续按链表后移节点
pre = cur
cur = cur.next
6.3 链表与顺序表的对比
链表只能记录头节点地址,因此在访问,尾部插,中间查时,都需要从头节点,遍历过去,所以复杂度O(n):
- 链表可以利用离散的空间,顺序表只能开辟完整的连续空间,只要list不够,必须重新开辟
- 链表时间花费到遍历地址上,顺序表花费到表的复制搬迁

6.4 双向链表
对于前面单向的,当前node不能查看其前面node的信息,所以引入双向。添加,删除node时,要保证每个node中的P,N都 给上值,如:中间插入.
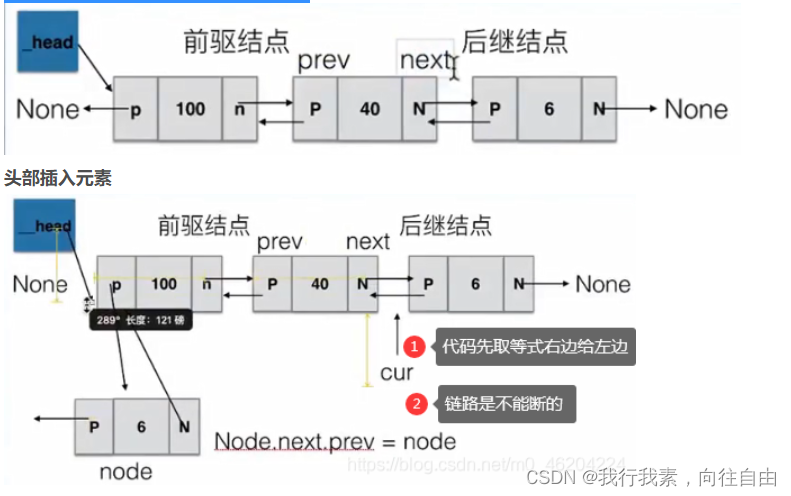
def add(self, item):
"""头部插入元素"""
node = Node(item)
if self.is_empty():
# 如果是空链表,将_head指向node
self._head = node
else:
# 将node的next指向_head的头节点
node.next = self._head
# 将_head的头节点的prev指向node
self._head.prev = node
# 将_head 指向node
self._head = node
尾部插入元素:
def append(self, item):
"""尾部插入元素"""
node = Node(item)
if self.is_empty():
# 如果是空链表,将_head指向node
self._head = node
else:
# 移动到链表尾部
cur = self._head
while cur.next != None:
cur = cur.next
# 将尾节点cur的next指向node
cur.next = node
# 将node的prev指向cur
node.prev = cur中间插入:
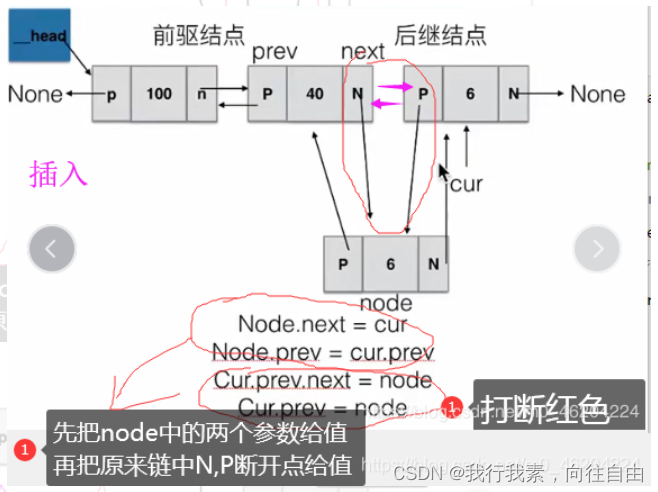
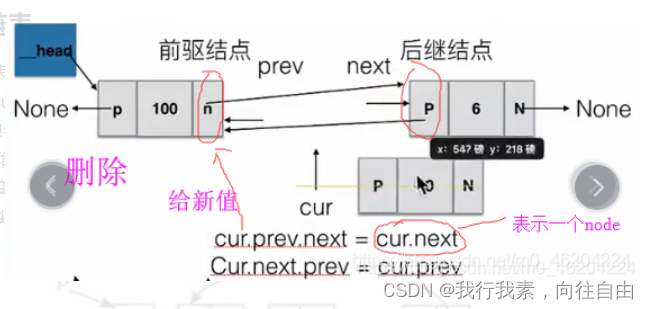
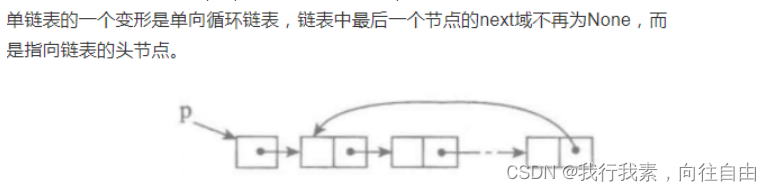
6.5 单向循环链表
- 由于是循环列表,最后的尾结点不再是None结束,而是指向self._head
- 由于一开始将cur = self._head设成游标,所以判断语句只能是cur.next
- while cur.next != self._head
使用cur.next不能进到循环体,会导致少一次打印,可以手动打印
length(self)返回链表长度: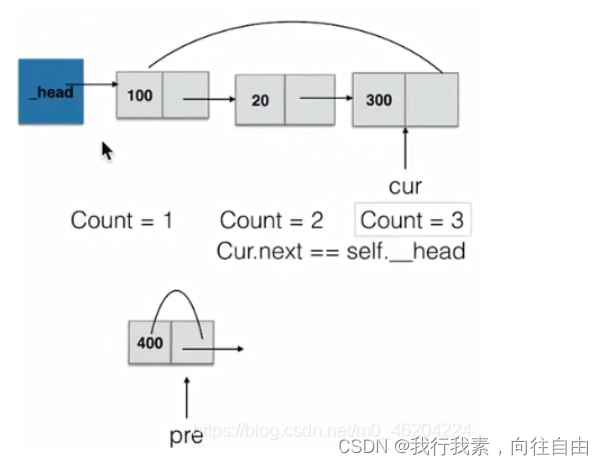
def length(self):
"""返回链表的长度"""
# 如果链表为空,返回长度0
if self.is_empty():
return 0
count = 1
cur = self._head#指针启动地址
while cur.next != self._head:#因为循环链表最后一个node要带有self._head,所以通过判断是否有self._head来看是否一个循环结束
count += 1
cur = cur.next
return count
头部添加节点:
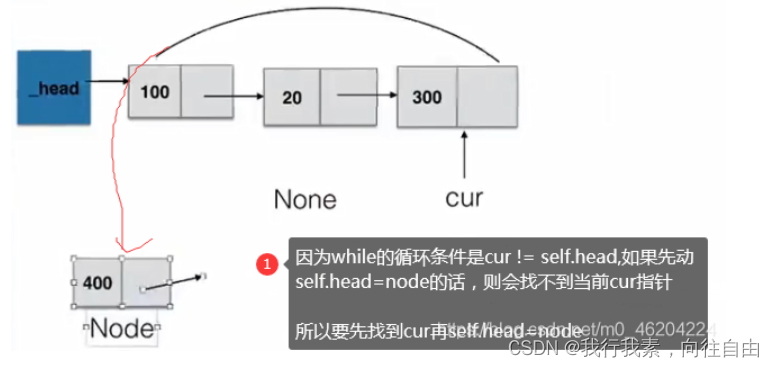
def add(self, item):
"""头部添加节点"""
node = Node(item)
if self.is_empty():
self._head = node
node.next = self._head
else:
#添加的节点指向_head
node.next = self._head
# 移到链表尾部,将尾部节点的next指向node
cur = self._head
while cur.next != self._head:
cur = cur.next
cur.next = node
#_head指向添加node的
self._head = node
7.栈
栈=杯
顺序表,链表是用来存数据的
栈和队列不考虑数据是如何存放的,栈stack,队列是一种容器,执行什么样的操作,抽象结构。
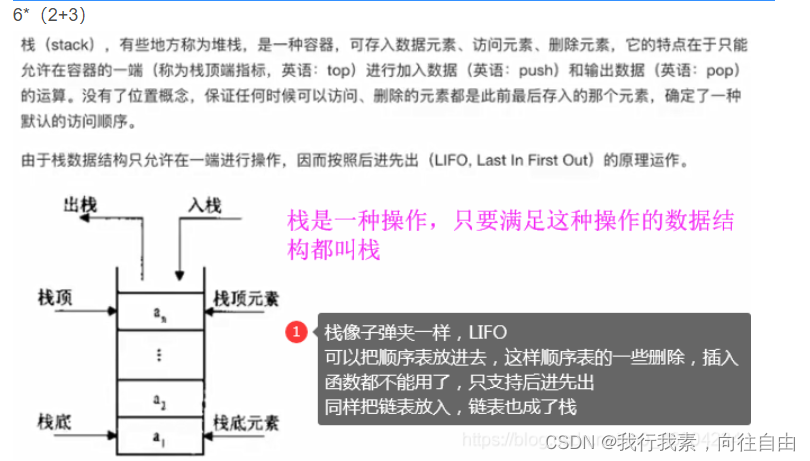

#利用前面封装好的顺序表的二次开发
class Stack(object):
"""栈"""
def __init__(self):#初始化的时候要生成一个容器,顺序表就是python中的list,然后再执行操作,可将list设成私有的,self.__items = []这样就不能修改原来的list容器
self.items = []
def is_empty(self):
"""判断是否为空"""
return self.items == []#右边是一个判断返回True
#对于存放的数据结构是顺序表来讲,尾部压栈出栈复杂度为o(1),对于链表来讲,头部复杂度为o(1),所以要考虑
def push(self, item):#从尾部压,从尾部取
"""加入元素"""
self.items.append(item)
def pop(self):
"""弹出元素"""
return self.items.pop()
def peek(self):
"""返回栈顶元素"""
return self.items[len(self.items)-1]
def size(self):
"""返回栈的大小"""
return len(self.items)
if __name__ == "__main__":
stack = Stack()
stack.push("hello")
stack.push("world")
stack.push("itcast")
print stack.size()
print stack.peek()
print stack.pop()
print stack.pop()
print stack.pop()
8.队列


#因为出入队总有一个复杂度为N,所以考虑是出队用的多,还是入队多,再写程序
class Queue(object):
"""队列"""
def __init__(self):#空列表保存队列
self.items = []
def is_empty(self):
return self.items == []
def enqueue(self, item):
"""进队列"""
self.items.insert(0,item)
def dequeue(self):
"""出队列"""
return self.items.pop()
def size(self):
"""返回大小"""
return len(self.items)
if __name__ == "__main__":
q = Queue()
q.enqueue("hello")
q.enqueue("world")
q.enqueue("itcast")
print q.size()
print q.dequeue()
print q.dequeue()
print q.dequeue()
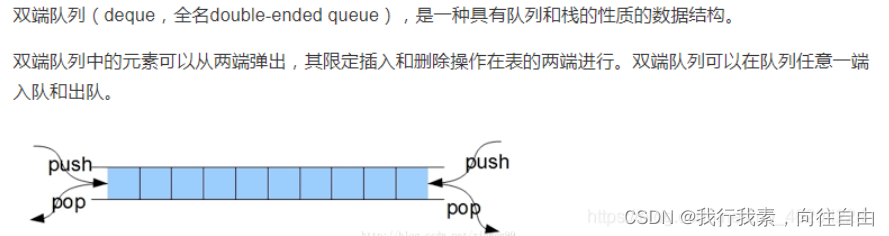
双端队列:两个栈尾部放一起

9.排序
接下来有兴趣了,继续更新。。。。。。