一种新的基于区域的在线活动轮廓模型研究（Matlab代码实现）

news2024/9/28 1:16:22

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

摘要：

该文提出一种新的基于区域的在线活动轮廓模型（ORACM）。经典测地线活动等值线（GAC）模型仅具有局部分割属性，尽管 Chan–Vese （C–V）模型具有全局性。Zhang， Zhang， Song， and Zhou （2010）中提出的最新的活动轮廓模型（ACM with SBGFRLS）既具有全局/局部分割的性质，又结合了GAC和C-V模型以提高活动轮廓在图像分割方面的性能。但是，它有两个主要缺点。首先，它仅使用迭代设置的当前水平的梯度使活动轮廓模型变形，因此工作速度太慢。其次，它需要一个参数α，该参数对结果有重大影响，并根据输入图像进行调整。所提出的模型ORACM通过使用新的二元水平集公式和新的正则化操作（如形态开合）消除了这两个缺点。在不改变分割精度的情况下，与传统的 ACM 相比，ORACM 不需要任何参数和更少的时间。在合成和真实图像上的实验表明，ORACM在形态学操作下的计算成本平均比传统ACM低3.75倍。

稳健而快速的图像分割步骤对消费者（Subašić，Lončarić，&Heđi，2012）和医学图像处理（Lai and Chang，2009，Vard等人，2011）的应用结果产生重大影响。已经提出了许多分割技术，其中主动计数器模型（ACM）（Zhang等人，2010，Chan和Vese，2001，Caselles等人，1997，Tseng等人，2009）是最成功的方法之一。ACM的主要思想是通过最小化与内部和外部能量之和相关的能量，从嘈杂的图像中描绘出物体轮廓。现有的ACM方法可分为两类（Chan和Vese，2001，Li等人，2007，Lie等人，2006，Zhang等人，2010）和基于边缘的（Brox等人，2010，Caselles等人，1997，Osher和Fedkiw，2002，Tseng等人，2009）。）模型。基于区域的方法从图像分割到明确定义的区域中得出计数器表示，而基于边缘的方法则考虑到边界点可以通过差分属性作为图像梯度来表征，并且计数器表示可以拟合到边界点。在基于区域的方法中，首先确定用户定义的曲线，然后使用能量最小化算法使活动计数器模型变形，直到其拟合对象边界。在基于边缘的方法中，如果像素通过数值测试，例如图像梯度的局部最大值，则像素属于边界（Ronfard，1994）。

与基于边缘的方法相比，基于区域的方法具有许多优势，因此通常是首选。一个优点是，基于区域的模型利用等值线内部和外部的统计信息来更新活动等值线。因此，它们对噪点不太敏感，对于边缘较弱或没有边缘的图像具有更好的性能。其次，他们试图同时检测外部和内部边界，并且它们对初始轮廓的位置的敏感性显着降低（Zhang等人，2010）。

由于编码的许多优点，如内在的、无参数的和隐式的，水平集方法（Brox等人，2010，Lie等人，2006，Osher和Fedkiw，2002，Zhang等人，2010）提供了一种直接的方式来估计演化结构的几何性质，可以改变拓扑结构。水平集方法可用于以隐式方式有效地解决曲线/曲面传播问题。总之，它们提供了一个非常方便的框架以及基于区域的主动轮廓模型来解决图像分割问题。

该文提出一种基于区域的在线活动轮廓模型（称为ORACM），该模型采用新的水平集公式。简而言之，与传统的ACM相比，ORACM的优势可以表示为在不改变精度比的情况下提供更少的时间，并且没有参数。

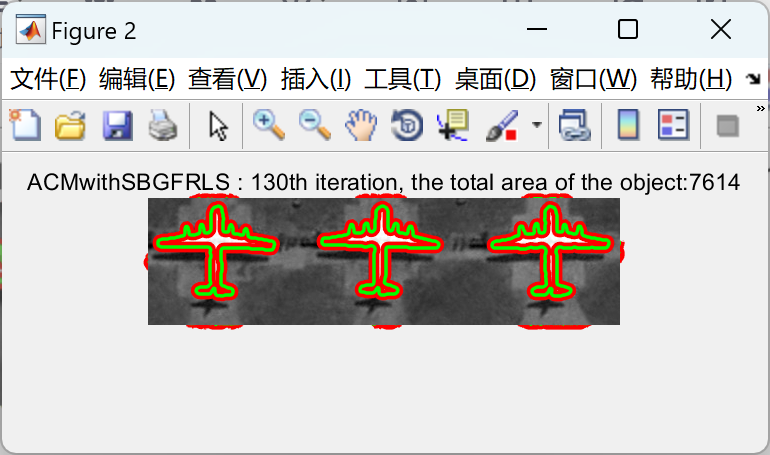
📚2 运行结果

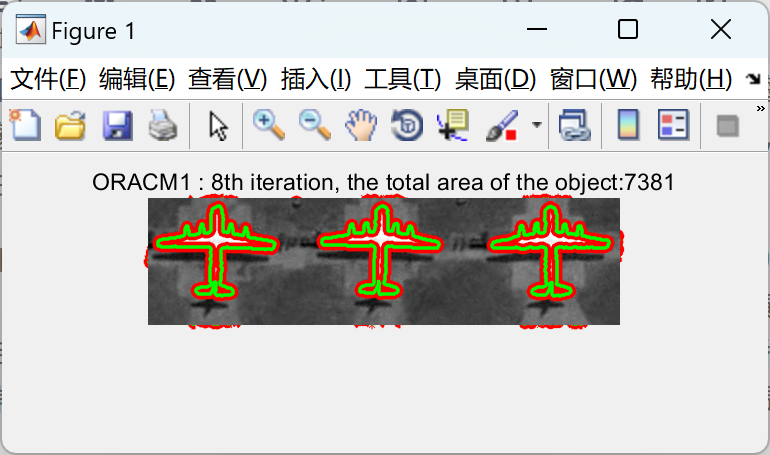
部分代码；

function [time,itr] = ACMwithSBGFRLS(Img,show)
[row,col] = size(Img);
u = -ones(row,col);
u(10:row-10,10:col-10) = 1;
sigma = 1; G = fspecial('gaussian', 5, sigma);
delt = 1; mu = 10;itr = 0;
objPos = u >= 0; objNeg = ~objPos;
Area1 = sum(u(:)); Area2 =0;
if show,
figure;imshow(Img,[]); hold on;
contour(u, [0 0], 'r','LineWidth',4);hold on;
contour(u, [0 0], 'g','LineWidth',1.3);hold on;
title(['ACMwithSBGFRLS : ',int2str(itr),'th iteration, the total area of the object:',int2str(abs(Area2))]);axis off;
end
tic