617. 合并二叉树

class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
root = TreeNode()
if not root1 and not root2:
return
elif root1 and not root2:
root = root1
elif not root1 and root2:
root = root2
elif root1 and root2:
root.val = root1.val + root2.val
root.left = self.mergeTrees(root1.left, root2.left)
root.right = self.mergeTrees(root1.right,root2.right)
return root
700.二叉搜索树中的搜索
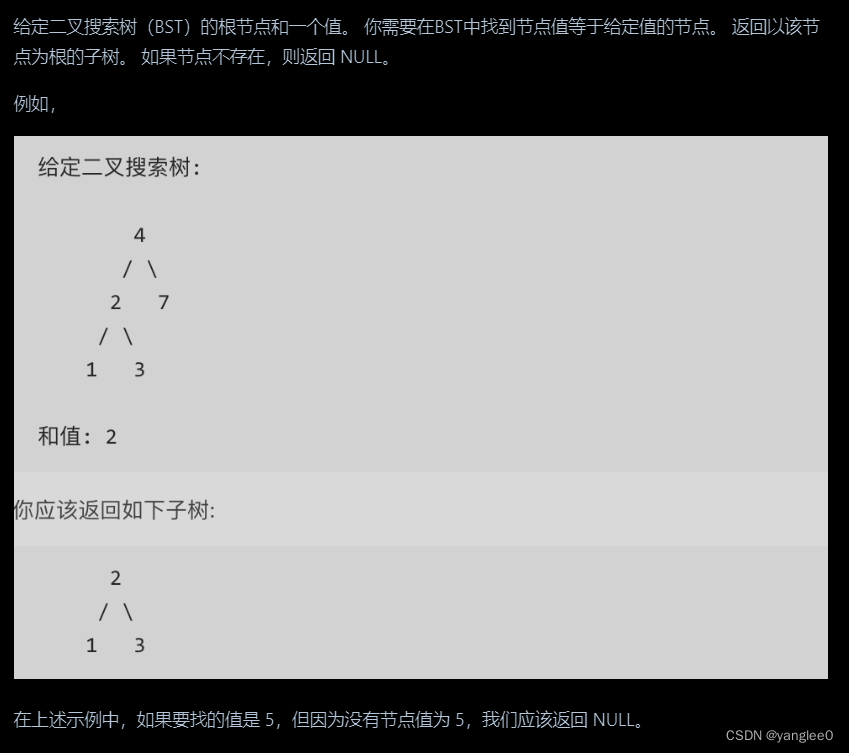
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root or root.val==val:
return root
if root.val<val:
return self.searchBST(root.right,val)
elif root.val>val:
return self.searchBST(root.left,val)
98.验证二叉搜索树
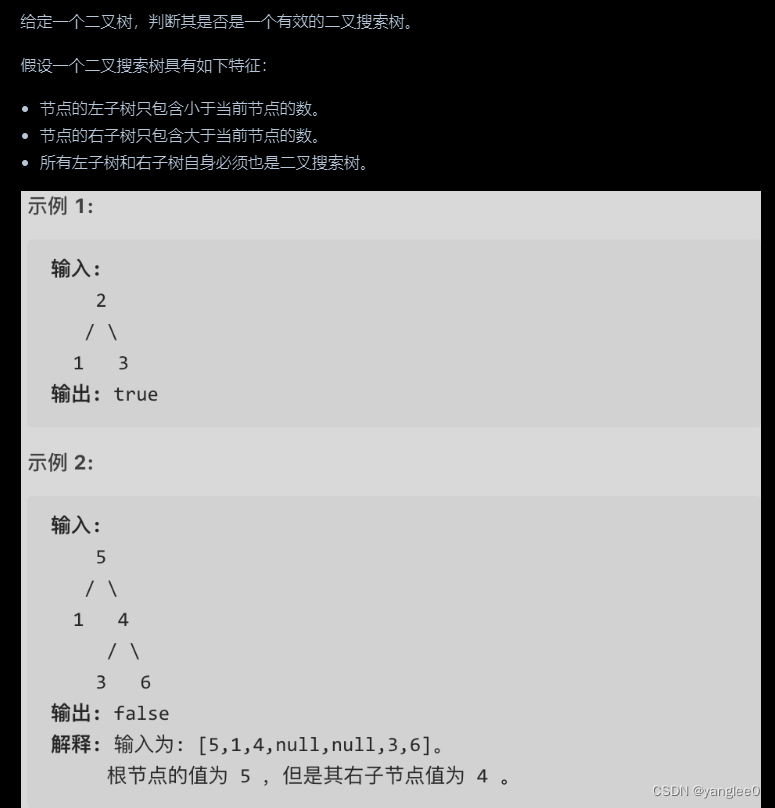
class Solution:
def __init__(self):
self.valid = float('-inf')
def isValidBST(self, root: Optional[TreeNode]) -> bool:
# 中序遍历的结果一定是从小到大,否则为false
if not root:
return True
left = self.isValidBST(root.left)
if self.valid<root.val:
self.valid = root.val
else:
return False
right = self.isValidBST(root.right)
return left and right
530.二叉搜索树的最小绝对差

class Solution:
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
# 先中序遍历,在找到差值最小的两个值之间。因为二插搜索树的中序遍历是从小到大,所以两两找就可以找到差值最小值了。
res = []
def dfs(root):
if not root:
return
dfs(root.left)
res.append(root.val)
dfs(root.right)
dfs(root)
min_value = res[-1]
for i in range(len(res)-1):
min_value = min(min_value,res[i+1]-res[i])
return min_value
501.二叉搜索树中的众数
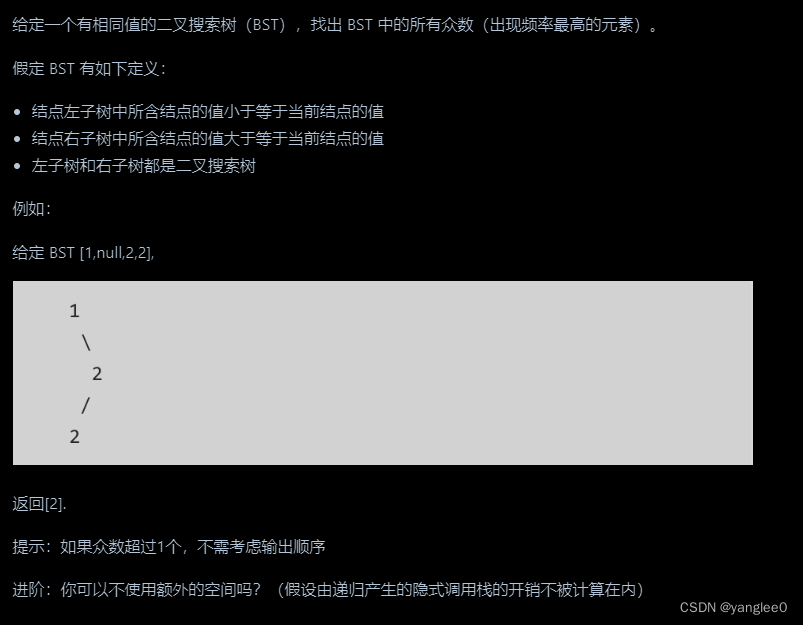
class Solution:
def findMode(self, root: Optional[TreeNode]) -> List[int]:
# 先中序遍历,在按照counter的次数进行排序,返回计数最大的几个值。
res = []
def dfs(root):
if not root:
return
dfs(root.left)
res.append(root.val)
dfs(root.right)
dfs(root)
final_statics = collections.Counter(res)
sorted_value = sorted(final_statics.items(),key=lambda x:x[-1],reverse = True)
res = []
for key,value in sorted_value:
if value == sorted_value[0][1]:
res.append(key)
return res
236. 二叉树的最近公共祖先
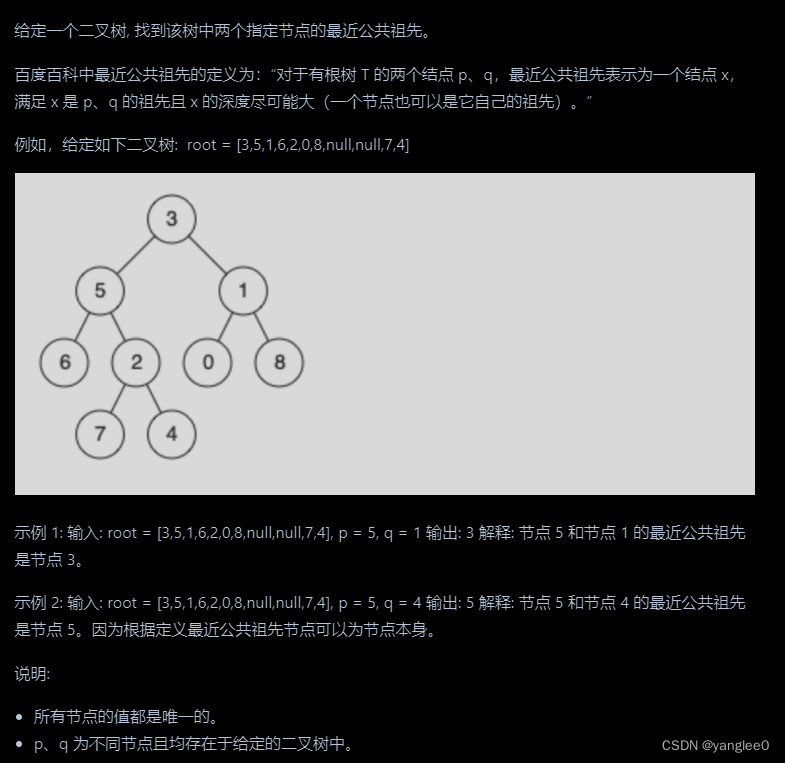
详细看代码随想录中本题题解
思路:
- 求最小公共祖先,需要从底向上遍历,那么二叉树,只能通过后序遍历(即:回溯)实现从底向上的遍历方式。
- 在回溯的过程中,必然要遍历整棵二叉树,即使已经找到结果了,依然要把其他节点遍历完,因为要使用递归函数的返回值(也就是代码中的left和right)做逻辑判断。
- 要理解如果返回值left为空,right不为空为什么要返回right,为什么可以用返回right传给上一层结果。
如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。
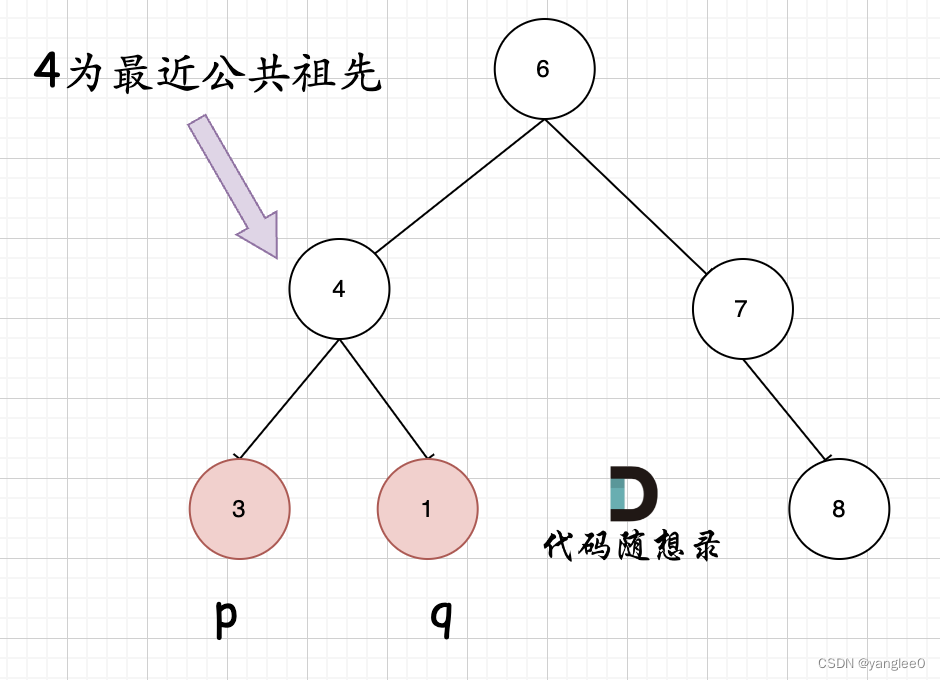
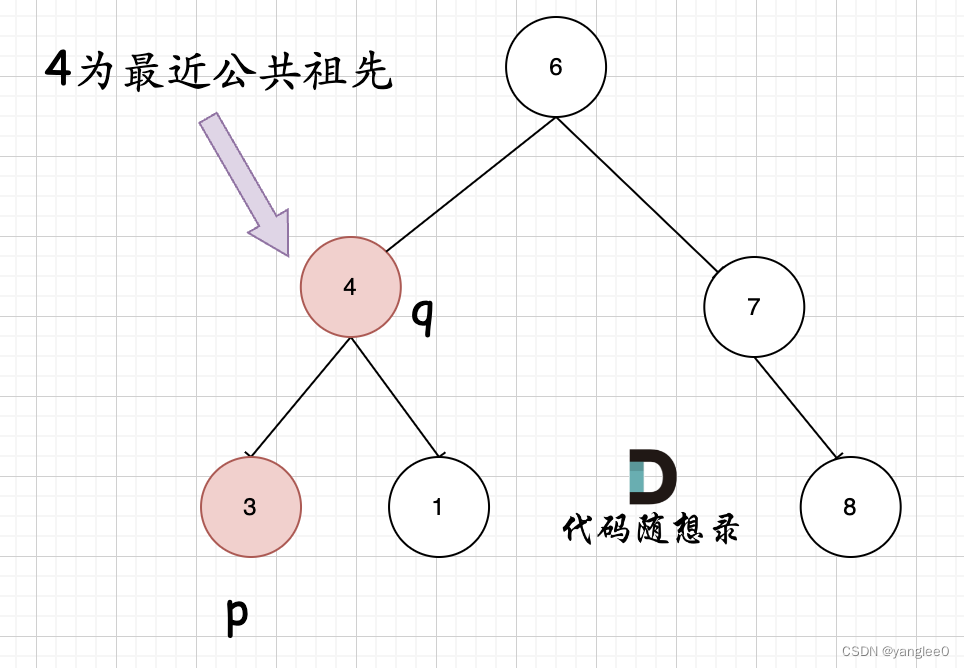
递归三部曲:
1、确定递归函数返回值以及参数
lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
2、确定终止条件
遇到空的话,因为树都是空了,所以返回空。
那么我们来说一说,如果 root == q,或者 root == p,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到,那么中节点的处理逻辑,下面讲解。
if (root == q || root == p || root == NULL) return root;
3、确定单层递归逻辑 (是遍历一边?还是遍历整颗树?)
PS:

本题中,在递归函数有返回值的情况下:如果要搜索一条边,递归函数返回值不为空的时候,立刻返回,如果搜索整个树,直接用一个变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯)。

如果left 和 right都不为空,说明此时root就是最近公共节点。这个比较好理解
如果left为空,right不为空,就返回right,说明目标节点是通过right返回的,反之依然。
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if p==root or q==root or not root: # 要么返回p,要么返回q,要么返回空。
return root
left = self.lowestCommonAncestor(root.left,p,q)
right = self.lowestCommonAncestor(root.right,p,q)
if left and not right:
return left # 如果左存在,右与空,则说明左侧中包含p/q,先找到的本身就是最近祖先
if right and not left:
return right # 如果左为空,右存在,则说明右侧中包含p/q,先找到的本身就是最近祖先
if left and right:
return root # 这里注意返回的是root,也就是祖先,而不是返回left/right
450.删除二叉搜索树中的节点

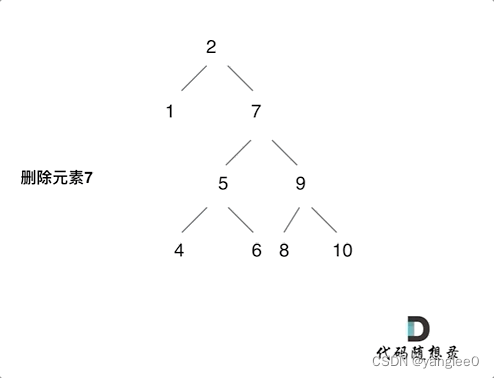
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root: # 没找到删除的节点,遍历到空节点直接返回了
return root
if root.val == key: # 找到删除的节点
if root.right and not root.left: # 删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
return root.right
elif root.left and not root.right: # 删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
return root.left
elif root.left and root.right: # 既有左孩子,也有由孩子的情况
cur = root.right
while cur.left is not None: # 找到右子树最左下角的一个
cur = cur.left
cur.left = root.left
return root.right
else: # 左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
return None
if root.val>key: # left
root.left = self.deleteNode(root.left,key)
if root.val<key:
root.right = self.deleteNode(root.right,key)
return root
701.二叉搜索树中的插入操作

class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
subTree = TreeNode(val = val)
return subTree
if root.val>val:
root.left = self.insertIntoBST(root.left,val) # 关键点:注意返回值要接住
if root.val<val:
root.right = self.insertIntoBST(root.right,val) # 关键点:注意返回值要接住
return root
450.删除二叉搜索树中的节点


class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root: # 没找到删除的节点,遍历到空节点直接返回了
return root
if root.val == key: # 找到删除的节点
if root.right and not root.left: # 删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
return root.right
elif root.left and not root.right: # 删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
return root.left
elif root.left and root.right: # 既有左孩子,也有由孩子的情况
cur = root.right
while cur.left is not None: # 找到右子树最左下角的一个
cur = cur.left
cur.left = root.left
return root.right
else: # 左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
return None
if root.val>key: # left
root.left = self.deleteNode(root.left,key)
if root.val<key:
root.right = self.deleteNode(root.right,key)
return root
701.二叉搜索树中的插入操作

class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
subTree = TreeNode(val = val)
return subTree
if root.val>val:
root.left = self.insertIntoBST(root.left,val) # 关键点:注意返回值要接住
if root.val<val:
root.right = self.insertIntoBST(root.right,val) # 关键点:注意返回值要接住
return root






![[STL]详解list模拟实现](https://img-blog.csdnimg.cn/img_convert/d0485487dcf0b76b3eaf15eaa7220ebb.png)