Wasserstein Distance, Contraction Mapping, and Modern RL Theory | by Kowshik chilamkurthy | Medium
一、说明
数学家们在考虑一些应用的情况下探索的概念和关系 - 几十年后成为他们最初从未想象过的问题的意想不到的解决方案。 黎曼的几何学只是出于纯粹的原因才被发现的——完全没有应用,后来被爱因斯坦用来解释时空结构和广义相对论。
二、RL强化学习概念
强化学习(RL)中,智能体为顺序决策问题寻求最佳策略。 强化学习的常用方法,它模拟了对这种回报或价值的期望。 但是,在 “分布RL”旗帜下的RL的最新进展侧重于代理收到的随机返回R的分布。 状态操作值可以显式视为随机变量 Z,其期望值为 Q
![]()
方程1:普通贝尔曼操作员B
普通贝尔曼算子 B (Eq-1) 通过迭代最小化 Q 和 BQ 之间的 L 平方距离(TD 学习),在近似 Q 值方面起着至关重要的作用。
![]()
方程2:分布贝尔曼算子ⲧπ
类似地,分布贝尔曼算子 ⲧπ 通过迭代最小化 Z 和 ⲧπ Z 之间的距离来近似 Z 值。
Z 和 ⲦπZ 不是向量,而是分布,如何计算 2 个不同概率分布之间的距离? 答案可能很多(KL,DL指标等),但我们对Wasserstein距离特别感兴趣。
三、什么是瓦瑟斯坦距离
俄罗斯数学家列昂尼德·瓦塞尔施泰恩(Leonid Vaseršteĭn)于1969年提出了这一概念。 瓦瑟斯坦距离是两个概率分布之间距离的度量。 它也被称为推土机距离,EM距离的缩写,因为非正式地,它可以被解释为移动和转换一堆泥土的最小能量成本,以一种概率分布的形状转变为另一种分布的形状。
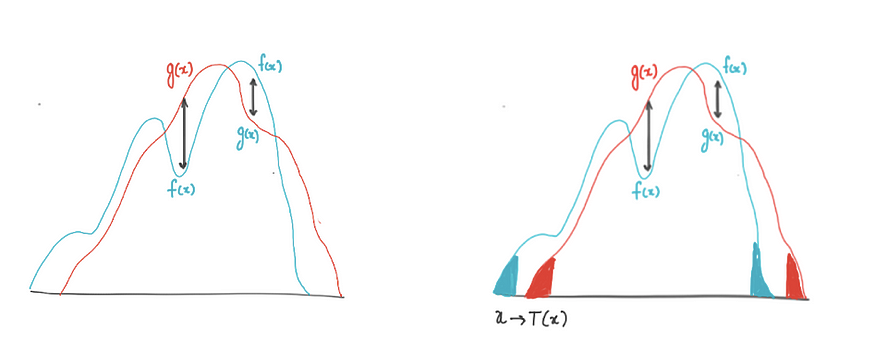
推土机的距离,图片来源:作者
累积分布函数 F、G 之间的瓦瑟斯坦度量 (dp) 定义为:

方程3:瓦瑟斯坦度量
其中下确界取用所有随机变量对(U,V),具有各自的累积分布F和G.dp(F,G)也写为:

方程4:瓦瑟斯坦度量
例
让我们先看一个简单的情况:假设我们有两个离散分布 f(x) 和 g(x),定义如下:
f(1) = .1, f(2) = .2, f(3) = .4, f(4) = .3 g(1) = .2, g(2) = .1, g(3) = .2,g
(4) = .5
让我们计算方程 3:δ0 = 0.1–0.2 = -0.1 δ1= 0.2–0.1 = 0.1–2.0 = 4.0 δ2= 0.2–3.0 = 3.0
δ5= 0.2–<>.<> = -<>.<> 中定义的 Wasserstein 度量 (dp)
因此 Wasserstein metric (dp) =∑|δi|=0.6
四、为什么选择瓦瑟斯坦距离
与Kullback-Leibler散度不同,Wasserstein度量是一个真实的概率度量,考虑了各种结果事件的概率和距离。与KL-散度等其他距离指标不同,Wasserstein 距离提供了分布之间距离的有意义且平滑的表示。
这些属性使 Wasserstein 非常适合结果的潜在相似性比完全匹配可能性更重要的域。
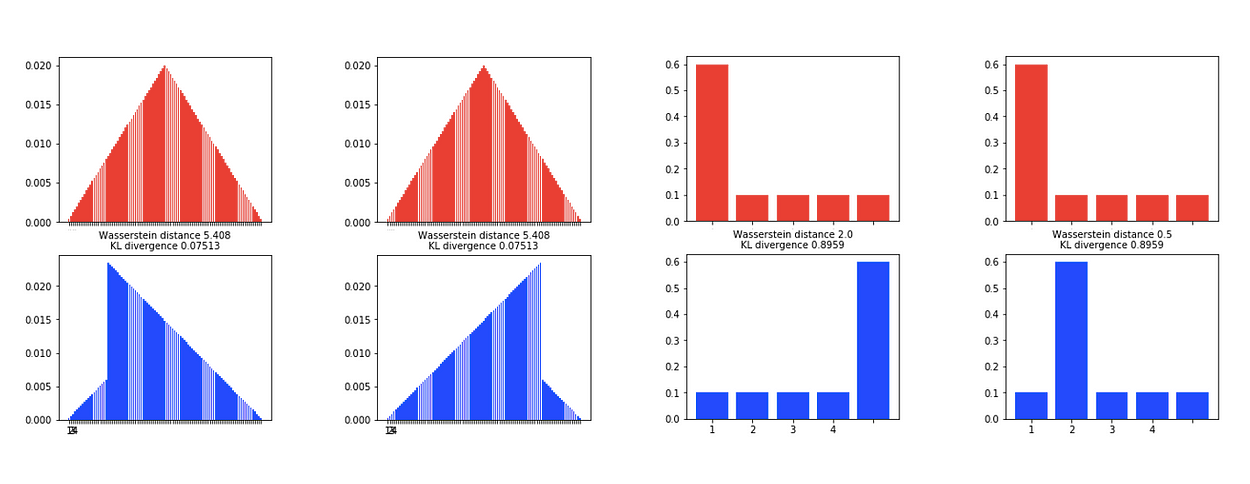
Python 生成的示例,图片来源:作者
右图:对于KL散度,红色和蓝色分布之间的测量值相同,而Wasserstein距离测量将概率质量从红色状态传输到蓝色状态所需的功。
左图:瓦瑟斯坦距离确实有问题。只要转移,距离就保持不变,无论转移发生什么方向,概率质量都保持不变。因此,我们没有办法对距离进行推理。
五、ɣ-收缩
收缩映射在强化学习的经典分析中起着关键的数学作用。让我们首先定义收缩
5.1 收缩映射
在度量空间的元素上定义的函数(或运算符或映射)是收缩,如果存在一些常量 ɣ,使得对于度量空间 X₁ 和 X₂ 的任何两个元素,以下条件成立:(X, d)
![]()
公式5:收缩映射
这意味着在元素 X₁ 和 X₂ 上应用映射 f(.) 后,它们彼此之间的距离至少增加了一个因子 ɣ 。
5.2 RL 收缩
证明收缩非常重要,因为它证明了距离度量本身的使用是合理的。分布运算符 ⲧπ 用于估计 Z(x,a),证明 ⲧπ 是 dp 的收缩意味着所有矩也以指数方式快速收敛。

方程6:ɣ收缩
收缩表明,将运算符 Ⲧ 应用于 2 个不同的分布会缩短它们之间的距离,因此距离度量的选择非常重要。现在让我们尝试证明“分布算子 ⲧπ” 是 Wasserstein 距离 (dp) 的收缩。
5.3 证明
Wasserstein度量的3个重要性质有助于我们证明收缩。

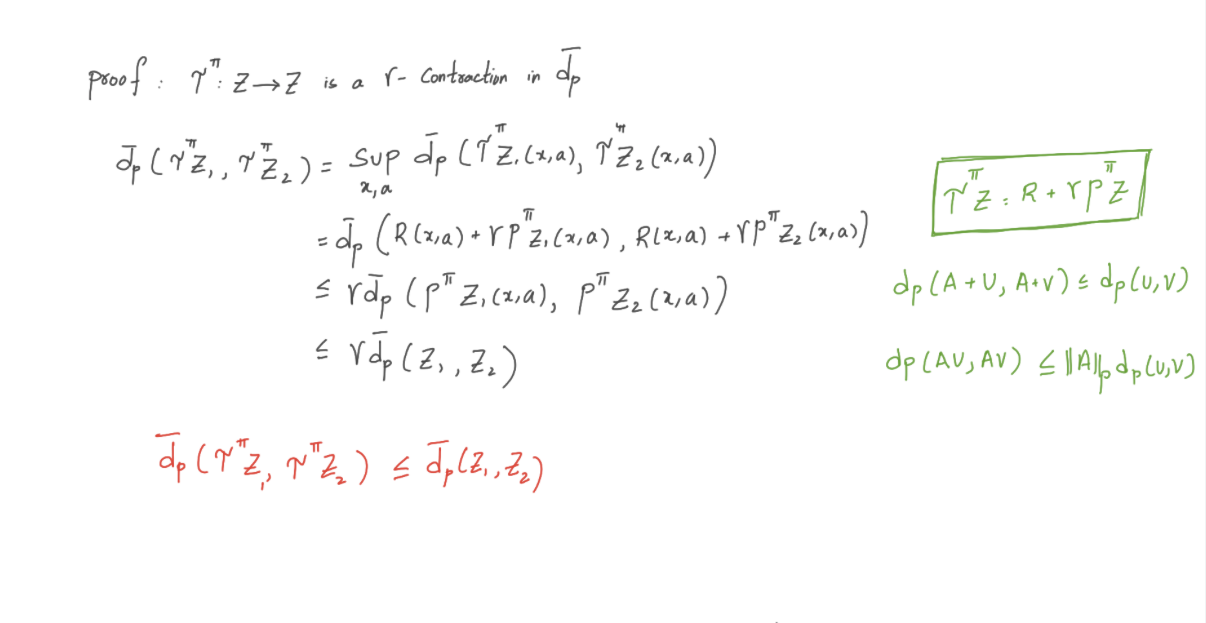
六、结论
在这篇博客中,我们定义了瓦瑟斯坦距离,讨论了它的优缺点。 我们通过证明它的收缩来证明它在分布贝尔曼算子中作为距离度量的使用是合理的。 但这只是开始的结束,Wasserstein距离在计算随机梯度时提出了挑战,这使得它在使用函数近似时无效。 在我的下一篇博客中,我将讨论如何使用分位数回归来近似 Wasserstein 度量。
七、引用
- distributions - What is the advantages of Wasserstein metric compared to Kullback-Leibler divergence? - Cross Validated
- https://runzhe-yang.science/2017-10-04-contraction/#contraction-property
3. 强化学习的分布视角






![[STL]详解list模拟实现](https://img-blog.csdnimg.cn/img_convert/d0485487dcf0b76b3eaf15eaa7220ebb.png)