2023牛客暑期多校-J-Qu‘est-ce Que C‘est?（DP)

news2024/9/23 5:22:17

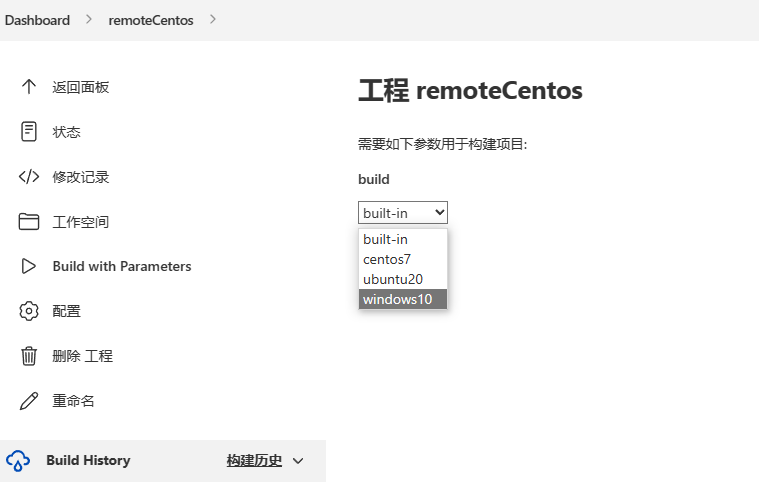
题意：

给定长度为n的数列 ${a}_{i=1}^{n}$ ,要求每个数都在 $[-m,m]$ 的范围，且任意长度大于等于2的区间和都大于等于0，问方案数。 $1\leq n,m\leq 5\times 10_{}^{3}$ 。

思路：

首先要看出是dp题， $dp[i][x]$ 用来表示遍历到第i位且后缀和最小为x的可行方案数（此时的后缀可以只有最后一位）。很显然j的值在区间 $[-m,m]$ 。下面考虑dp如何转换：

1.对于 $x\epsilon [0,m]$ 。先讨论 $dp[i][0]$ ， $dp[i][0]$ 可由 $dp[i-1][j],j< 0$ 加一位值为 $-j$ 转换而来；也可由 $dp[i-1][j],j>=0$ 加一位值为0 转换而来。就有 $dp[i][0]=\sum_{j=-m}^{m} dp[i-1][j]$ 。再讨论 $dp[i][1]$ ，可由 $dp[i-1][j],j<0,1-j\leq m$ ，加一位值为 $1-j$ 转换而来；也可由 $dp[i-1][j],j>=0$ 加一位值为1转换而来。就有 $dp[i][1]=\sum_{j=1-m}^{m} dp[i-1][j]$ 。依次讨论可以得出 $dp[i][x]$ 可以由 $dp[i-1][j],j< 0,x-j<=m$ ,末位加值为 $x-j$ 转换而来；也可由 $dp[i-1][j],j>=0$ ，末位加x转换而来。综上所诉： $dp[i][x]=\sum_{j=x-m}^{m} dp[i-1][j]$

2.对于 $x\epsilon [-m,0)$ 。可以去验证，只有 $dp[i-1][j],j>=-x$ ,末位加值为x才能转换成 $dp[i][x]$ 。所以 $dp[i][x]=\sum_{j=-x}^{m}dp[i-1][j]$ 。

为了方便计算我们把 $[-m,m]$ 这个区间平移映射到 $[0,2m]$ 区间上。按照上述思想去找新的dp转换式就有：

$dp[i][x]=\sum_{j=x-m}^{2m}dp[i-1][j],x\varepsilon [m,2m]$

$dp[i][x]=\sum_{j=2m-x}^{2m}dp[i-1][j],x\epsilon [0,m)$

由于都是求和到2m，所以可以考虑后缀和优化。

代码：

//#define _CRT_SECURE_NO_WARNINGS 
//#include<iostream>
//#include<algorithm>
//#include<cstdio>
//#include<map>
//#include<string.h>
//#include<string>
//#include<vector>
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 998244353;
const int N = 5005;
ll dp[N][N*2];//dp[i][j]表示遍历到i位，后缀和最小为j且合法的数量。（这里后缀和包含了只含有最后一位的情况）
ll sum[N * 2];//后缀数组
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n, m;
	cin >> n >> m;
	ll ans = 0;
	//初始化
	for (int i = 0; i <= m*2; i++)
	{
		dp[1][i] = 1;
	}
	for (int i = 2; i <= n; i++)
	{
		//处理后缀和
		for (int j = m * 2; j >= 0; j--)sum[j] = (sum[j + 1] + dp[i - 1][j]) % mod;
		//[0,m）的情况
		for (int j = 0; j < m; j++)
		{
			dp[i][j] = sum[2 * m - j];
		}
		//[m,2m]的情况
		for (int j = m; j <= 2 * m; j++)
		{
			dp[i][j] = sum[j - m];
		}
	}
	//统计
	for (int i = 0; i <= m * 2; i++)
	{
		ans = (ans + dp[n][i]) % mod;
	}
	cout << ans << endl;
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/807149.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！