一)组合总和

377. 组合总和 Ⅳ - 力扣（LeetCode）

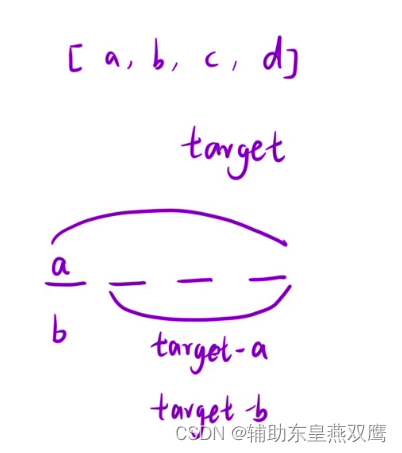
排列:所有情况是有序的

组合:所有情况是无序的

一)定义一个状态表示:

有限制条件下的组合问题:

1)dp[i][j]表示从前i个物品中进行挑选，总体积不超过j，所有的选法中，要的是最大的价值

但是这个状态表示没有规定挑选的顺序，第一个位置挑选什么，第二个位置挑选什么，仅仅是在所有的选法中要的是最大的价值，因此在这些选发中本质上是没有顺序的，所以背包问题本质上解决的是一个组合问题，因此此排列问题不能用背包问题解决；

2)这道题非常像背包问题，依旧是给定一些数从里面挑，限定条件就是目标和，每一个数都是可以无限使用的，因此这个题非常像完全背包问题

3)之前在做动态规划的时候，定义状态标识都是使用线性dp来进行解决的，或者是以区间dp来进行解决的，以某一个位置为结尾巴拉巴拉，以某一个位置为起点巴拉巴拉，或者是选取一段区间，巴拉巴拉

4)还可以根据分析问题的过程中，发现重复子问题，抽象出来一个状态表示，

dp[i]就表示凑成组合数是i，一共有多少种排列数

二)根据状态标识推到状态转移方程:

1)dp[i]=dp[i-nums[j]]，以j位置为结尾，要找的是总和为i的最小排列数，那么只是需要去总和为i-nums[i]的排列数即可

2)在所有总和是i-nums[j]为结尾的所有情况中后面拼接上一个nums[j]即可

3)dp[i]+=dp[i-nums[j]](i>=nums[j])

 

 三)初始化+填表顺序(从左向右)+返回值(dp[target])

dp[0]表示从选择组合数是0的方案个数，什么都不选，选择一个1个空集，就是一种方案，所以dp0]=1，如果初始化等于0，那么根据状态转移方程，后面的数都是等于0的

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp=new int[target+1];
        dp[0]=1;
        for(int i=1;i<=target;i++){
            for(int j=0;j<nums.length;j++){
                if(i-nums[j]>=0)
                dp[i]+=dp[i-nums[j]];
            }
        }
    return dp[target];
    }
}

二)不同的二叉搜索树

96. 不同的二叉搜索树 - 力扣（LeetCode）

左子树<根节点<右子树

一)定义一个状态表示在分析问题的过程中发现重复子问题，抽象出来一个状态标识

之前想看看有5个结点的时候一共有多少种二叉搜索树，但是当我固定完成一个根节点3的时候左子树有两个节点的时候有多少种二叉搜索树，右子树有两个结点的时候有多少种二叉搜索树，所以分析思路就是当某一个节点是某一个数的时候，左子树是N-1个结点的时候有多少种二叉搜索树，右子树是i-(n-1)个结点的时候有多少种二叉搜索树

所以dp[i]就表示以节点个数为i的时候一共有多少种二叉搜索树

二)根据状态标识推到状态转移方程:

1)当我们进行选择节点数是i的时候一共有多少种二叉搜索数，那么1-i中间的数都是有可能充当根节点的

2)根节点是j，左边的节点个数是dp[j-1]，右边的节点个数是dp[i-j]，所以当根节点是j的时候，左子树的节点数量是j-1，右子树的节点数量就是i-j；

三)初始化

dp[0]=1，当节点个数是0的时候，就是一颗空树，空树也是可以被认为是一种二叉搜索树

如果你的dp[0]!=1的话，那么根据你的状态转移方程后面的值都是0

class Solution {
    public int numTrees(int n) {
     int[] dp=new int[n+1];
     dp[0]=1;
     for(int i=1;i<=n;i++){
         for(int j=1;j<=i;j++){
             dp[i]+=dp[j-1]*dp[i-j];
         }
     }
      return dp[n];
    }
}