本篇文章介绍了符号距离函数Signed Distance Funciton(SDF),占用场Occupancy Field,神经辐射场Neural Radiance Field(NeRF)的概念、联系与区别。
显式表示与隐式表示
三维空间的表示形式可以分为显式和隐式。
比较常用的显式表示比如体素Voxel,点云Point Cloud,三角面片Mesh等。
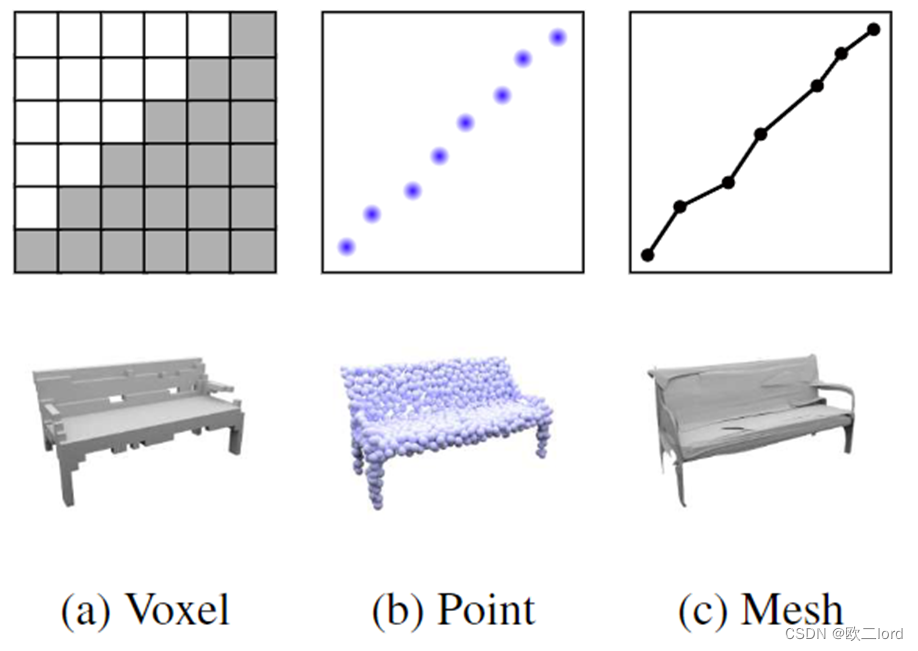
比较常用的隐式表示有 符号距离函数Signed Distance Funciton(SDF),占用场Occupancy Field,神经辐射场Neural Radiance Field(NeRF) 等。
本文将对几种隐式表示进行介绍,并以我本人的理解讲一讲它们的联系和区别。
概述
首先,对这三种隐式表示进行概述,帮助大家对三种表示有一个大致的认识,这里看不懂没关系,后面有更加详细的介绍。
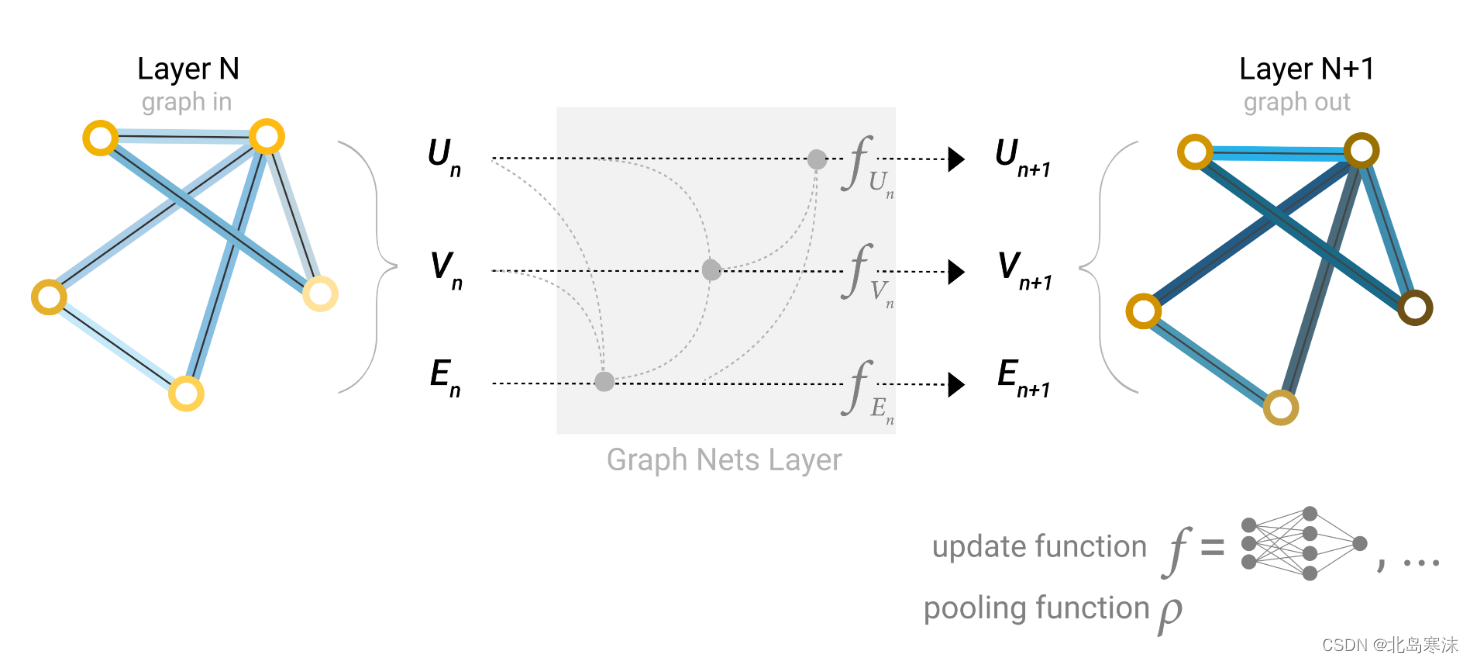
函数function与场field
先回顾一下函数和场的概念,我认为函数和场实际上都是代表了一种映射关系。
函数 f(x)=y 是自变量 x 到因变量 y 的映射。
场的定义是向量到向量或数的映射,空间中的场可以认为是空间中点到这个点的属性的映射。以磁场为例,磁场就是空间中每个点都具有一个磁感应矢量B,也就是点到向量的映射,即空间中每个点都映射到一个特定的向量 B B B。在其他情况下,点不一定映射到向量,也可以映射到标量或者其他属性,只要是空间中点到属性的映射都是空间场。( 一般用坐标 ( x , y , z ) (x,y,z) (x,y,z)表示空间中的点,所以点到属性的映射实际上是 ( x , y , z ) (x,y,z) (x,y,z)到属性 s s s的映射,如场 F : ( x , y , z ) → s F: (x,y,z)→s F:(x,y,z)→s,这里的 s s s可以是向量也可以是标量)
本文讲的三种隐式表示都可以看做是一种映射关系,而且我们都可以用神经网络去拟合这种映射关系,达到用神经网络去表示三维空间的目的。
Signed Distance Funciton(SDF)
Signed Distance Funciton对应的中文是“符号距离函数”,我们更常见到的是它的缩写SDF。
SDF表示一个点到一个曲面的最小距离,同时用正负来区分点在曲面内外。点在曲面内部则规定距离为负值,点在曲面外部则规定距离为正值,点在曲面上则距离为0.
SDF的映射关系如下:

这里
x
x
x是个三维向量,代表三维空间中的点,
s
s
s是一个值。也就是说
S
D
F
SDF
SDF实际上是一个点到一个值的映射。
相应的 s < 0 s<0 s<0 则表示 x x x 在曲面内, s > 0 s>0 s>0表示 x x x 在曲面外, s = 0 s=0 s=0表示 x x x 在曲面上。我们就可以用 S D F ( x ) = 0 SDF(x)=0 SDF(x)=0 来表示一个曲面。
Occupancy Field
占用场表示一个点是否被曲线占用(占用就是在曲面内部)。
占用场的映射关系如下:

这里的 p p p是空间中的点, s s s表示 p p p被曲面占用的概率。可以看到占用场的映射关系和SDF是一致的,它和SDF的区别在于,占用场的 s s s的取值是 [ 0 , 1 ] [0,1] [0,1],即必须在0,1之间,所以占用场是将一个三维空间映射到 [ 0 , 1 ] [0,1] [0,1],即:

通常以0.5为标准,即占用概率 s s s大于0.5我们倾向于认为点被曲面占用, s s s小于0.5我们倾向于认为点没有被曲面占用, s s s等于0.5我们认为点在曲面上。所以我们可以用 F ( p ) = 0.5 F (p)=0.5 F(p)=0.5 在连续的三维占用场中表示一个曲面。
Neural Radiance Field
Neural Radiance Field 神经辐射场是这几年很火的概念,主要是由于NeRF以及后续系列工作的优异表现。
辐射场就是将“点+这个点发出的一条射线”映射到“点的密度值+射线的方向对应的颜色值”,映射关系如下:

x
,
y
,
z
x,y,z
x,y,z表示点坐标,
d
d
d表示从这个点发出的一条射线的方向,
R
,
G
,
B
R,G,B
R,G,B表示从这个射线的方向去看这个点的颜色值,
σ
\sigma
σ表示这个点的密度值(比如烟雾的密度比较低,固体点的密度就很高)。
而神经辐射场,就是用神经网络去拟合辐射场的映射关系。
下面将详细介绍每个隐式表示:
Signed Distance Funciton(SDF)
SDF在2D和3D中都有应用,我们可以先看一下SDF在2D中的形式,了解其在2D上的应用会对理解其在3D中的表示有帮助。
Signed Distance Funciton表示带符号的距离函数,其实还有不带符号的距离函数,也就是Unsigned Distance Funciton,2D中的Unsigned Distance Funciton可以表示如下:

这里黑色的就是表示的形状,在Unsigned Distance Funciton下,形状内部的点的距离会被定义为0,而形状外部的点的值代表了这个点到形状的最短距离。
相对于Unsigned Distance Funciton,Signed Distance Funciton增加了正和负的概念,内部和外部的点的绝对值都代表了点到形状的距离,这时内部的点不再都是0,而是用负值表示,外部的点的值用正值表示。如下图所示:

这张图红色的表示在形状外部的点,绿色代表在形状内部的点,黑色代表边界,可以看到黑色两侧的点的值的正负发生了变化,也就是说 S D F = 0 SDF=0 SDF=0表示的曲线可以代表形状的边界。
理解了二维的SDF,就可以类推到三维的SDF,可以想象一个空间,空间中有正值和负值的点,而正负点的交界处就可以认为是空间曲面。
这里展示一张《DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation》(CVPR2019)