A:模拟

 

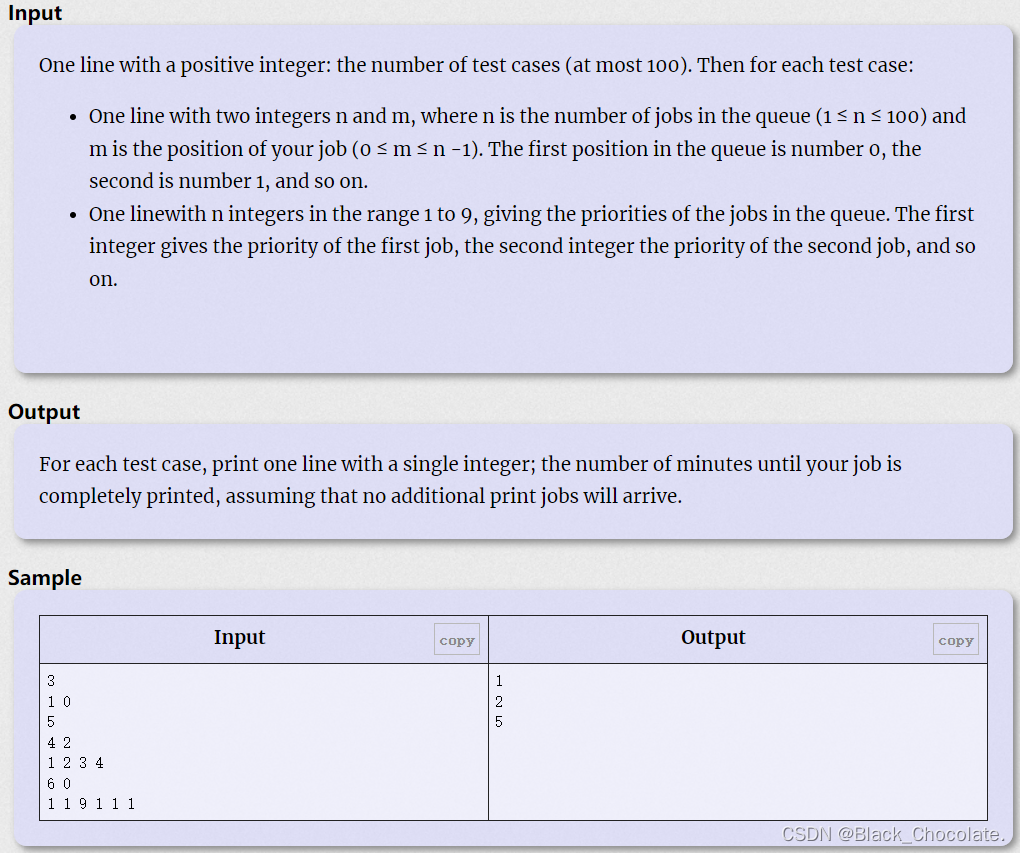
题意：给定了N个任务，每个任务都有一个优先级（1~9），数字越大，优先级越高。将这些任务放入队列中，如果出队的元素（x），x的优先级不是最高的，那么就将x放入队尾，依次进行这种操作。再给定一个数字M，代表第几个任务，规定从下标0开始，且每一个任务的打印时间都为1，问要打印第M个任务，需要的时间是多少？（任务的出队和入队操作不计时） 

分析：这题的题意已经说的很明白了，模拟这一过程就行了

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#define PII pair<int,int>
using namespace std;
const int N=110;
int a[N];

struct Node{
	int val,pos;
};

inline void solve(){
	int n,m;cin>>n>>m;
	queue<Node>q;
	for(int i=0;i<n;i++){
		cin>>a[i];
		Node ee;
		ee.val=a[i];ee.pos=i;
		q.push(ee);
	}
	sort(a,a+n,greater<int>());//从大到小记录一下任务的优先级：因为只有优先级最高的才会打印
	int ans=1,top=0;
	while(!q.empty()){
		Node cc=q.front();
		q.pop();
		if(cc.val==a[top]&&cc.pos!=m) ans++,top++;//如果满足打印条件，且不是目标任务
		else q.push(cc);//不满足打印条件，放入队尾
		if(cc.pos==m&&cc.val==a[top]) break;//满足打印目标任务，break
	}
	cout<<ans<<"\n";
}

int main(){
	int T;cin>>T;
	while(T--) solve();
}

B:哈密尔顿距离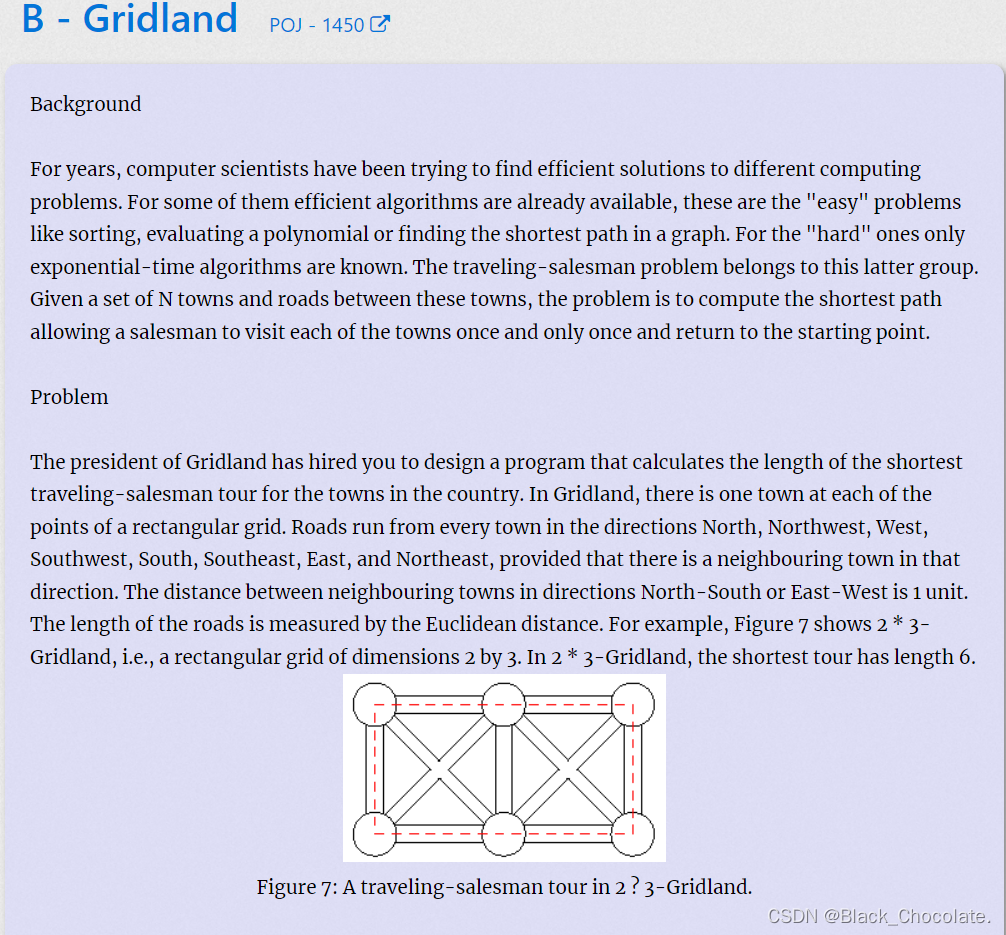

题意：给一些点，而这些点是有规律的排列（如图），现在从一个点出发，遍历所有的点，最后回到起点，但是途中不能重复经过某些点，其实就是哈密尔顿回路。求最短路径。

结论：关于哈密尔顿回路有一个小规律，那就是当n.m至少有一个是偶数时，最短路径就是n*m。否则就是n*m-1+sqrt(2)。（读者有兴趣可以推一下哦，很简单的推理）

代码：

#include <iostream>
#include <cstdio>
#include<algorithm>
using namespace std;
 
int main(){
    int T;
    double n,m;
    scanf("%d",&T);
    int i=1;
    while(T--){
        scanf("%lf%lf",&n,&m);
        printf("Scenario #%d:\n",i++);
        if((int)m%2==0 ||(int)n%2==0) printf("%.2lf\n",m*n);
        else printf("%.2lf\n",n*m+0.41);
        printf("\n");
    }
}

C:博弈论

题意：有N堆石头,每堆石头数目在1到100之间，最多有10堆.两人分别取走石头.

取石头的规则是：每次只能从1堆中取,每次取走至少1个。

取过后还可以把这堆的石头任意分配到其它石子数不为0的堆上，当然也可以不分配。

问给定这些石头堆的情况，两人轮流取，谁取走最后一个石子谁胜利，问是先取的胜利还是后取的胜利.双方最优策略。

分析：这里可以从经典的石子游戏Nim进行推理：

ps：因为石子是不断减少的，所以不存在平局。

我们这里寻找必胜态

1：当石子只有一堆时：先手必胜

解释：因为，先手可以直接选择取完整堆石子。后手没有石子可取，即：先手必胜

2：当石子只有两堆，且两堆的数目相同时：后手必胜

解释：先手取后肯定不会分配石子，因为一旦分配，那么就只剩下一堆石子，后手必胜。

先手是聪明的，所以每次都会只取不分，然而，后手只需要模仿先手的操作，那么先手是肯定赢不了的。（给组样例：）

3：当石子只有三堆时：先手必胜

解释：可以通过2进行推出，先手可以取后再分，将三堆石子化成情况2，这样，后手就成了先手，因为后手必胜，所以先手必胜

4：当石子只有四堆时且可以分成两两相等的两堆时：后手必胜

解释：因为三堆是必胜态，所以只需要逼对方取完某一堆石子，那么自己就将获胜，当然两人都不是傻子，那么最后即将化为3堆的情况，一定是 1 1 1 1，谁取石子处于这种状态，那么必输

结论：当n为偶，且可以分成n/2对两两相等的石子时，先手必败，否则先手必胜

代码：

#include <iostream>
#include<algorithm>
using namespace std;
const int N=110;
int n;
int a[N];

int main(){
    while(cin>>n){
    	if(n==0) break;
    	for(int i=1;i<=n;i++) cin>>a[i];
    	if(n&1){
    		cout<<1<<"\n";continue;
		}
		bool ok=true;
		sort(a+1,a+1+n);
		for(int i=1,j=2;i<=n;i+=2,j+=2){
			if(a[i]!=a[j]) ok=false;
		}
		if(ok) cout<<"0\n";
		else cout<<"1\n";
    }
}

 D:规律

题意：一群小孩围成一个圈，老师顺时针发糖，分别每间隔0,1, 2, 3, 4……发一颗，问是否每个同学都有糖 

思路：数论：完全剩余系（本蒟蒻数论不好，所以不会推导，给读者推荐一篇推导的blog：

POJ 3372 Candy Distribution（数论）_v5zsq的博客-CSDN博客_poj candy

我的方法：手撸样例找规律

结论：只要是2的幂就为YES，否则为NO

代码：

#include <iostream>
#include<algorithm>
using namespace std;
const int N=110;
int n;
int a[N];

int main(){
    while(cin>>n){
    	if((n&(n-1))==0) cout<<"YES\n";
    	else cout<<"NO\n";
	}
}

E:简单数学题

题意：给出航线的长度，经济舱500公里以下算500公里，否则算实际里程。商务舱算实际里程×1.5。头等舱实际里程×2。根据给出的航班，求出总航线长

分析：具体看代码

ps：0代表着一个case的结束，0后应该输出结果。然后可以再输入下一个case，#代表整个程序的结束。

#include <cstdio>
#include <cstring>
 
int main(){
    int miles, ans;
    char ch;
    char from[100], to[100];
 
    ans = 0;
    while (scanf("%s", from), strcmp(from, "#") != 0){
        if(strcmp(from, "0") == 0){
            printf("%d\n", ans);
            ans = 0;
            continue;
        }
        scanf("%s %d %c\n", to, &miles, &ch);
        if (ch == 'F'){
            ans += miles * 2;
        }
        else if (ch == 'B'){
            ans += (int)(miles * 1.5 + 0.5);
        }
        else if (ch == 'Y'){
            if (miles < 500){
                ans += 500;
            }
            else{
                ans += miles;
            }
        }
    }
}