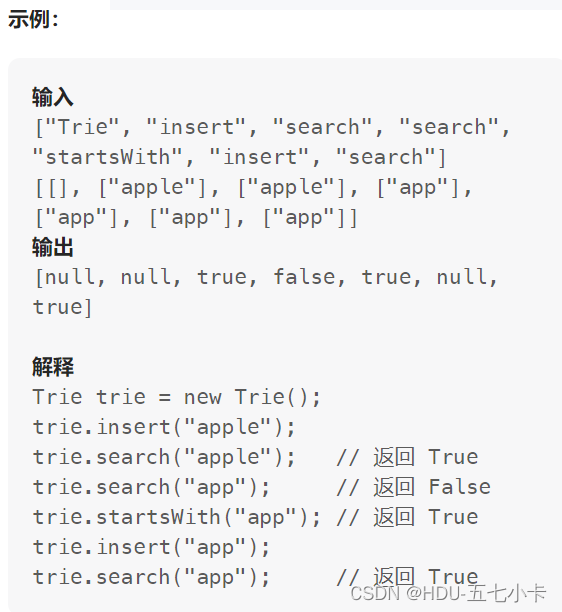
题目

Trie（发音类似 “try”）或者说 前缀树
是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。
请你实现 Trie类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix，返回 true ；否则，返回 false 。

思路

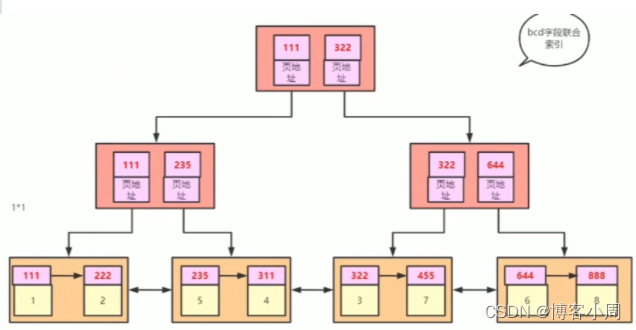
字典树（前缀树 / Trie树/单词查找树）：是一种树形结构，利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

下图就是一个字典树：

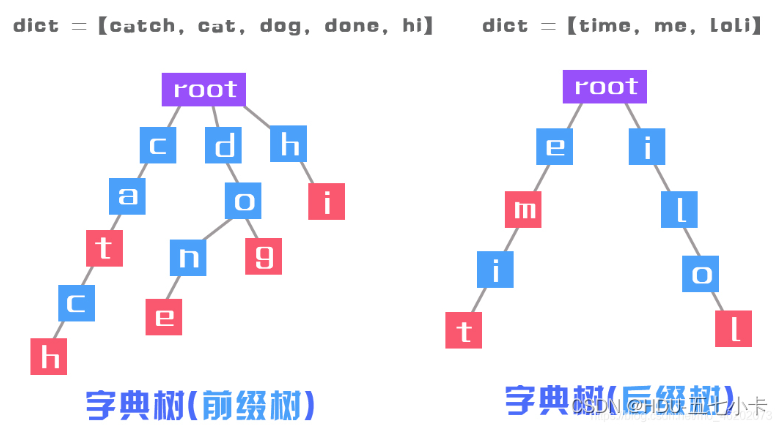
字典树的数据结构：

class TrieNode {
	boolean isWord;								// 从root根节点至此是否是一个完整的单词（即这个节点是否是一个单词的结尾）
	TrieNode[] children = new TrieNode[26];		// 巧妙的用数组的下标作为26个字母；数组的值则为子节点

	public TrieNode(){}		// 打酱油的无参构造函数(不写也行)
}

isWord为true的节点就是上面的图中红色的节点。举个例子，两个字符串"cat"和"catch"，字符 t 和字符 h 对应的节点，就是红色的

children[0] 对应小写字母 a，children[1] 对应小写字母 b，…，children[25]对应小写字母 z

插入字符串：
从根节点开始，对于当前字符串对应的子节点，有两种情况：

• 子节点存在：沿着指针到子节点，继续处理下一个字符
• 子节点不存在：创建一个新的子节点，记录在children数组的对应位置上，然后沿着指针移动到子节点，继续搜索下一个字符

查找前缀：
从根节点开始，对于当前字符串对应的子节点，有两种情况：

• 子节点存在，沿着指针移动到子节点，继续搜索下一个字符。
• 子节点不存在，说明字典树中不包含该前缀，返回空指针

重复以上步骤，直到返回空指针或搜索完前缀的最后一个字符

若搜索到了前缀的末尾，就说明字典树中存在该前缀。

此外，若前缀末尾对应节点的 isword 为真，则说明字典树中存在该字符串。

java代码如下：

class Trie{
	private Trie[] children;
	private boolean isWord;
	
	public Trie(){
		children = new Trie[26];
		isWord = false;
	}
	
	public void insert(String word){
		Trie node = this;//表示当前节点
		for(int i = 0; i < word.length(); i++){
			char ch = word.charAt(i);
			int index = ch - 'a';
			if(node.children[index] == null){
				node.children[index] = new Trie();
			}
			node = node.children[index];
		}
		node.isWord = true;
	}
		
	public boolean search(String word){
		Trie node = searchPrefix(word);
		return node != null && node.isWord;
	}

	public boolean startsWith(String prefix){
		return searchPrefix(prefix) != null;
	}
	
	private Trie searchPrefix(String prefix){
		Trie node = this;
		for(int i = 0; i < prefix.length(); i++){
			char ch = prefix.charAt(i);
			int index = ch - 'a';
			if(node.children[index] == null){
				return null;
			}
			node = node.children[index];
		}
		return node;
	}
}