NIM游戏

先看一下一维 NIM游戏。

有一堆大小为 n 的石子，甲和乙轮流从石堆里面拿石子，不能一次拿掉所有石子，取走最后一个石子的人获胜，甲先开始，谁是必胜的？

显然，谁先手，谁就获胜。那么推广到二维呢？

 

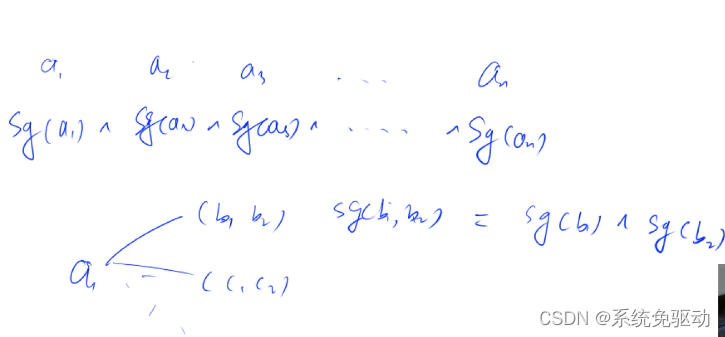
有两堆大小为 n m 的石子，甲和乙轮流从两个石堆里拿石子，每次从一个石堆里拿石子，不能一次拿掉一堆中所有石子，取走最后一个石子的获胜，甲先开始拿，谁是必胜的？

当 n=m 的时候，先手必输。因为先手从一堆中拿 Y 颗，后手也可以从另外一个堆中拿 Y 颗。循环下去，后手必胜。
而如果 n!=m，先手就可以制造两堆相等的石子，使得后手必败。

引入点新概念。当两堆相等时，先手必败，我们将这种状态叫做必败态。记为 P。
当两堆不相等时，先手必胜，将这种状态叫做必胜态，记为 N。

那么，推广到多维，如何确定谁是必胜的呢？
由前两种NIM游戏可以知道，如果所有石堆大小都相等，那么先手是不能直接取得胜利的。这种状态称为平衡态。反之，可以进行一次操作就取得胜利的状态就是非平衡态。平衡态也就是必败态，非平衡态也就是必胜态。
考虑将所有石堆的大小异或起来，如果结果为 0，那么这就是一个平衡态。如果结果不为零，那就是非平衡态。
我们每拿一次石子，都可以将异或时某一位上的值由这位上的 1 的奇偶性决定。因此我们拿石子时可以控制每一位上 1 的奇偶性，也就因此能控制异或出的总结果了。同样的，对手每操作一次，由于必须拿至少一颗石头，就势必将会影响某一位上 1 的数量，状态必然会改变。这就意味着我们在操作的时候，可以实现平衡态和非平衡态之间的转化。

如果一开始我们接手的是一个不平衡态，要取胜，就可以反复给对手构造一个平衡态，这是必胜的。
如果一开始接手的是一个平衡态，只要对手足够聪明，就可以让我们每次都拿到一个平衡态。这就是必败的。

SG函数

由刚才的论述可知，必胜态和必败态之间是可以相互转化的。必败态经过一次操作必然会转化为必胜态，必胜态经过一次操作可能是必胜态，也可能是必败态（想想异或的过程）。当一个状态已经转化为能够分出胜负的必败态时，称这个状态是0级必胜点，记作 SG(x)=0（x 描述了当前的状态）。
如果某个状态最少操作一次就能变为0级必胜点，那么这个状态就是1级必胜点，以此类推，有2级，3级……必胜点。而SG函数就是用来描述每个状态到达终末态时所需要的最少的步骤，即描述每个状态是几级必胜点。定义为：

SG(x)=MEX{SG(y)|x−>y}

SG定理

• 两个同级必胜点（SG函数值相等）组成的游戏是必败的。因为先手如果降低其中一个必胜点的等级，后手可以降低另一个必胜点的相同数量的等级，使先手一直面对两个同级必胜点，最后面对两个1级必胜点，只能将其中一个必胜点变成必败点，这样先手必败。

• 两个不同级必胜点（SG函数值不同）组合成的的游戏是必胜的，因为先手可以将等级高的必胜点的等级降低到与另一个必胜点相同，这样后手面对的就是由两个同级必胜点构成局面，先手必胜。

对于一个游戏，可以将组成它的每一个游戏的SG函数值异或起来，为 0，则对于先手来说必败，反之对于先手就是必胜的。这就是 SG定理了！

例题：

Fibonacci again and again

三堆大小分别为 n，m，p 的石子，每堆大小均不超过 1000，两个人拿，令 x 为菲波那契数列中的一项，每个人每次只能从一堆里拿 x 个石子，问谁是必胜的。

板题，主要想说说怎么记忆化搜索求SG函数值。

int sg[MAXN + 5],f[MAXN + 5];//f为菲波那契数列 int getsg(int num){ if(num == 0)return sg[num] = 0; if(sg[num] != -1)return sg[num]; bool vis[MAXN + 5];//表示从石子数为num可以转换到哪些状态 for(int i = 1; i <= MAXN: i++){ vis[num - f[i]] = 1; getsg(num - f[i]); } for(int i = 0; ; i++){ if(!vis[i])return sg[num] = i;//找mex，求出是几级必胜点 } return sg[num]; }

求出三个数的SG值后，看 SG(n)SG(m)SG(p) 是否为 0 即可得出答案。

A multiplication game

给定一个 n，令 p=1，甲和乙可以每次将 p 乘上一个属于 [2,9] 的数，谁使 p 大于 n 谁就赢。求谁是必胜的。

#include<iostream> #include<cstring> #include<map> #define int long long using namespace std; const int MAXN = 1e5; int n; map<int,int> sg,vis; int getsg(int x){ if(x >= n)return sg[x] = 0; if(vis.find(x) != vis.end())return sg[x]; vis[x] = 1; int s[10];//9的十次方已经大于n的最大值了，故sg函数的值最大为9 memset(s,0,sizeof s); for(int i = 2; i <= 9; i++){ s[getsg(x * i)] = 1; } for(int i = 0; i < 10; i++){ if(!s[i])return sg[x] = i; } return sg[x]; } signed main(){ while(~scanf("%lld",&n)){ sg.clear(); vis.clear(); getsg(1); if(sg[1])cout << "Stan wins.\n"; else cout << "Ollie wins.\n"; } }

Cutting Game

两个人在一张大小为 h∗w 纸上面切，每个人每次可以横着切一刀，也可以竖着切一刀，谁切出了 1∗1 大小的纸，谁就获胜，问谁必胜。

注意到状态是二维的，即当前纸的长与宽。注意下SG函数的记录方法。

#include<iostream> #include<cstring> using namespace std; const int MAXN = 1e3; int sg[MAXN + 5][MAXN + 6],n,m; int getsg(int x,int y){ if(x < y)swap(x,y); if(sg[x][y] != -1)return sg[x][y]; if(x == 1 && y == 1)return sg[x][y] = 1; bool vis[4001]; memset(vis,0,sizeof vis); for(int i = 2; i <= x - 2; i++){//横着切 vis[getsg(i,y) ^ getsg(x - i,y)] = 1;//每切一刀，就将当前纸分成了两张，也就是分成了两个子游戏，因此取异或的值 } for(int i = 2; i <= y - 2; i++){//竖着切 vis[getsg(x,i) ^ getsg(x,y - i)] = 1; } for(int i = 0; i <= 4000; i++){ if(!vis[i])return sg[x][y] = i; } return sg[x][y]; } int main(){ memset(sg,-1,sizeof sg); for(int i = 2; i <= MAXN; i++){ sg[1][i] = 0; } while(~scanf("%d%d",&n,&m)){ int ans = getsg(n,m); if(ans)cout << "WIN\n"; else cout << "LOSE\n";; } }