一、函数介绍
函数图像参考网站:Graphtoy
1.基本数学运算
| 函数 | 含义 | 示例图 |
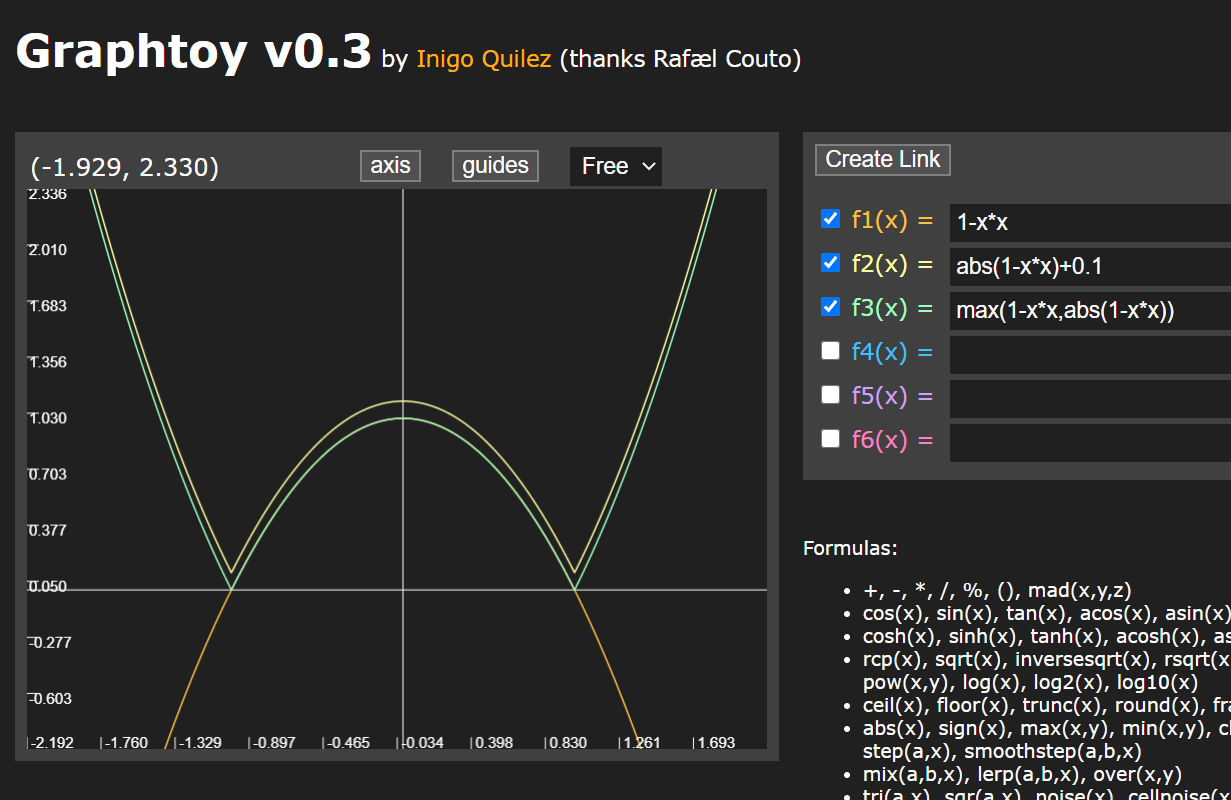
| min(a,b) | 返回a、b中较小的数值 | |
| mul(a,b) | 两数相乘用于矩阵计算 | |
| max(a,b) | 返回a、b中较大的数值 |
|
| abs(a) | 返回a的绝对值 | |
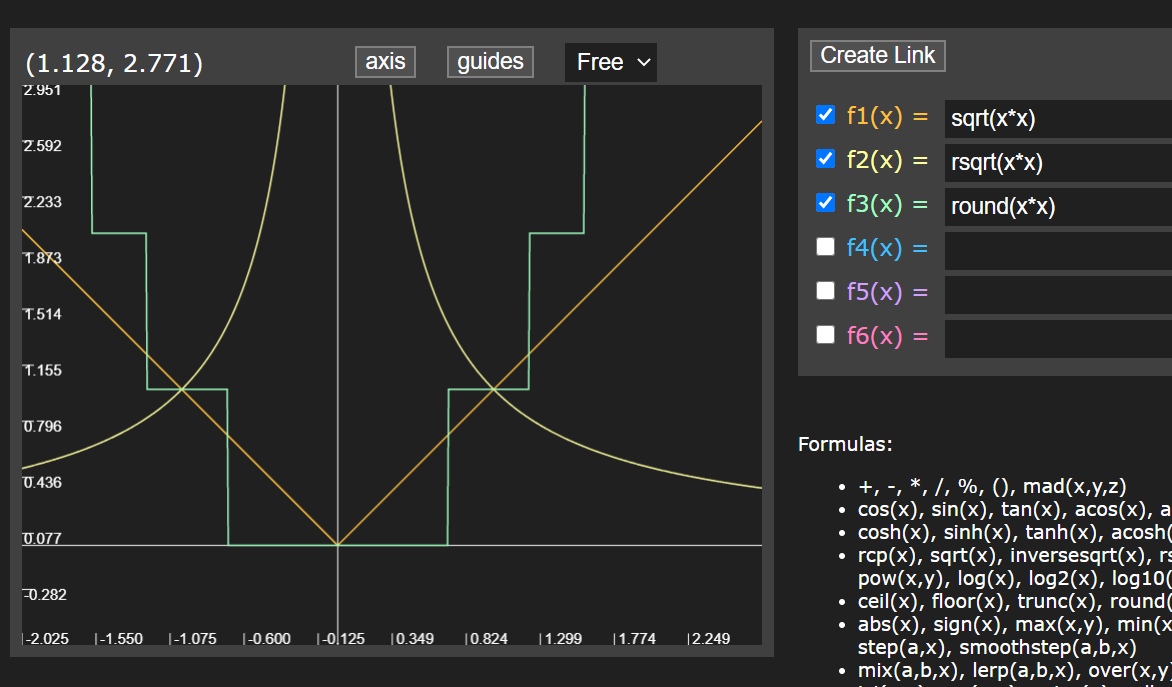
| round(x) | 返回与x最近的整数 |
|
| sqrt(x) | 返回x的平方根 | |
| rsqrt(x) | 返回x平方根的倒数 | |
| degregee(x) | 转换成弧度 | |
| redians(x) | 将角度转为弧度制 | |
| noise(x) | 噪声函数 |
2.幂指对与偏导数
| 函数 | 含义 | 示例图 |
| pow(x,y) | x的y次幂,xy |
|
| ldexp(x,exp) | 返回x与2的exp次方的乘积,x*2exp | |
| exp(x) | 返回以e为底的指数函数,ex | |
| exp2(x) | 返回以2为底的指数函数,2x | |
| log(x) | 返回x以e为底的对数,lnx | |
| log10(x) | 求以10为底的对数,log10x | |
| log2(x) | 求以2为底的对数,log2x | |
| frexp(x,out exp) | 把一个浮点数分解为尾数和指数, x : 要分解的浮点数据 返回值: 返回尾数 x = 尾数*2指数 (如果x参数为0,则此函数的尾数和指数均返回0) |
3.三角函数与双曲线函数
| 函数 | 含义 | 示例图 |
| sin(x) | 返回x的正弦值 | |
| cos(x) | 返回x的余弦值 | |
| tan(x) | 返回x的正切值 | |
| tan(y,x) | 返回y/x的正切值 | |
| sincos(x, out s, out c) | 返回x的正弦和余弦值 | |
| asin(x) | 返回x的反正弦值 |
|
| acos(x) | 返回x的反余弦值 | |
| atan(x) | 返回x的反正切值 | |
| atan2(y,x) | 返回y/x的反正切值 | |
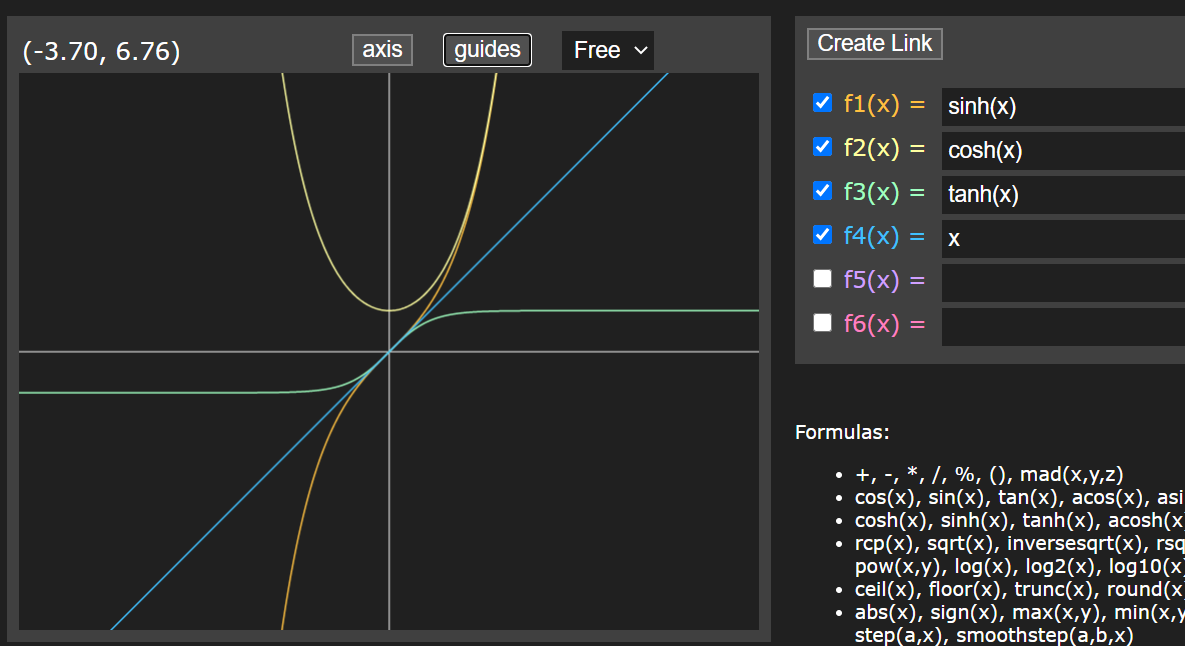
| sinh(x) | 返回x的双曲正弦值,0.5*(ex-e-x) |
|
| cosh(x) | 返回x的双曲余弦值 0.5*(ex-e-x) | |
| tanh(x) | 返回x的双曲正切值 |
4.数据范围
| 函数 | 含义 | 示例图 |
| ceil(x) | 返回>=x的最小整数 |
|
| step(x,y) | x<=y为1,否则为0 | |
| floor(x) | 返回小于或等于x的最大整数 | |
| saturate(x) | 返回将x限制在0和1之间的值 | |
| clamp(x,min,max) | 把x限制在[min,max]范围内,小于返回min,大于返回max | |
| frac(x) | 返回x的小数部分 | |
| fmord(a,b) | 返回a/b的浮点部分 | |
| modf(x,out ip) | 将值x分为小数和整数部分(各部分符号与x相同),ip返回整数部分,整体返回小数部分 | |
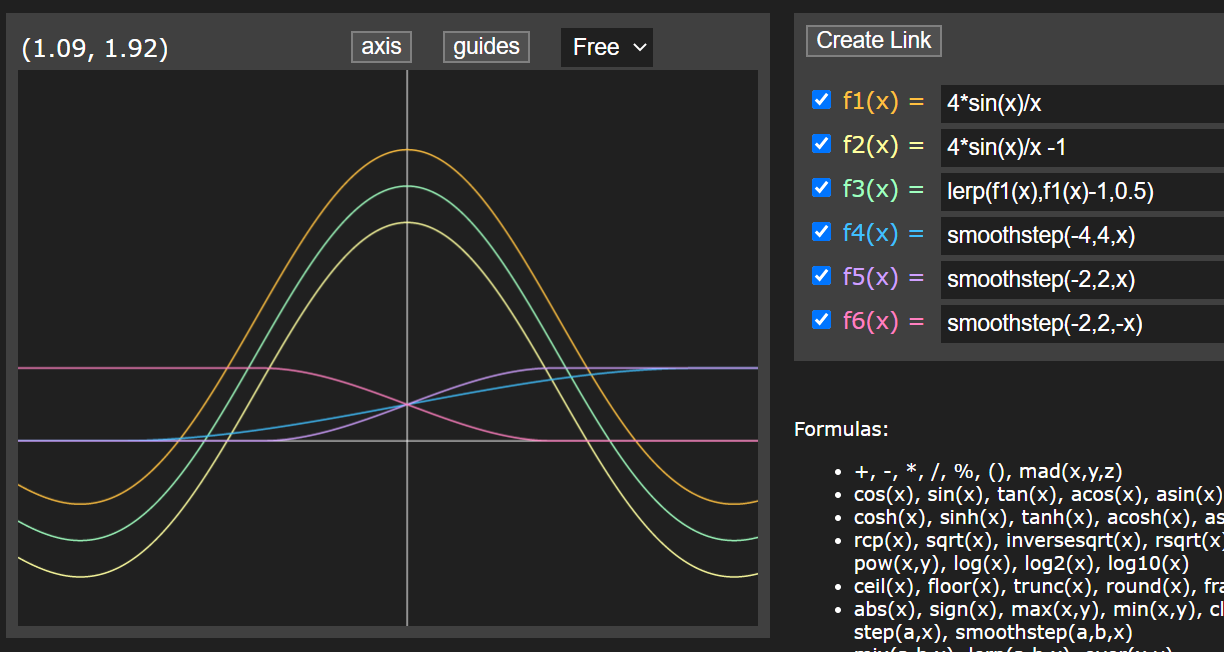
| lerp(a,b,s) | 按照s在a到b之间差值 |
|
| smoothstep(min,max,x) | 如果x在[min,max]范围内,则返回介于0~1之间的平滑Hermite差值;使用smoothstep HLSL内在函数在两个值之间创建平滑过渡。例如,使用此功能平滑的混合两种颜色 |
5.类型判断类
| 函数 | 含义 |
| all(x) | 确定指定量的所有分量是否均为非零,均非零则返回true,否则返回false(处理由浮点、整形、布尔型数据定义的标量,向量或者矩阵) |
| clip(x) | 如果输入值小于0,则丢弃当前像素,常用语判定范围(不仅仅针对0,返回值为void),常用于测试alpha,如果每个分量代表到平面的距离,还可以用来模拟剪切平面 |
| sign(x) | 返回x的正负性,如果x小于0返回-1,如果x等于0返回0,如果x大于0返回1 |
| isinf(x) | 如果x参数为+INF或者-INF(无穷+无穷仍无穷,0x3f3f3f3f),返回true,否则返回false |
| isfinite(x) | 判断x参数是有有界,有限的,与isinf(x)相反 |
| isnan(x) | 如果x参数为NAN(非数字),返回true,否则返回false |
6.向量与矩阵类
| 函数 | 含义 |
| length(v) | 返回向量的长度 |
| normalize(v) | 向量归一化,x/length(x) 方向向量归一化 |
| distance(a,b) | 返回两个向量之间的距离,按理说应该为0,此处表示为根号下各分量之差的平方和 |
| dot(a,b) | 返回a和b这两个向量的标积/内积/数量积/点积(a在b上的投影长,a·b=|a||b|·cosθ) |
| cross(a,b) | 返回a和b这两个向量的矢积/外积/向量积/叉积(返回值是个向量,而且与a、b都垂直,大小上|a×b| = |a| * |b| * sinθ) |
| determinant(m) | 返回指定浮点矩阵的按行列方式计算的值 |
| transpose(m) | 返回矩阵m的转置矩阵 |
7.光线运算类
| 函数 | 含义 | 示例图 |
| reflect(i, n) | 返回以i为入射向量n为法线方向的反射光 |
|
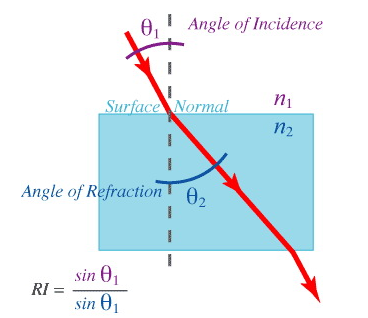
| refract(i, n, ri) | 返回以i为入射向量n为返现方向,ri为折射率的折射光 | |
| lit(n_dot_l, n_dot_h, m) | 输入标量(normal,light,半角向量h,镜面反射系数m),返回光照向量(环境光,漫反射光,镜面高光反射,1) | |
| faceforward(n, i, ng) | 得到面向视图方向的曲面法向量,输入输出为同源向量,返回 -n*sign(dot(i,ng))(normal,light,normal) |
8.1D纹理查找(几乎不会使用)
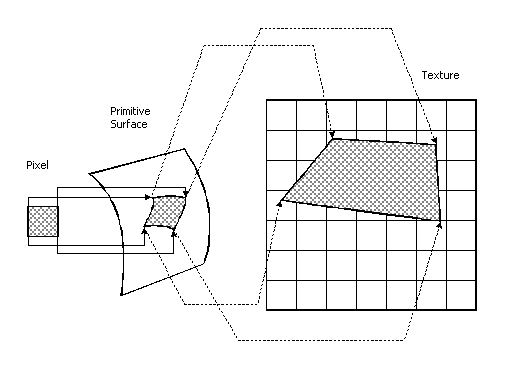
GPU在PS阶段是在屏幕空间XY坐标系中对每一个像素去对应的文立中查找对应的纹素确定像素的颜色。
《GPU 编程与CG语言之阳春白雪下里巴人》
| 函数 | 含义 | |
| tex1D(s,t) | 普通一维纹理查找,返回纹理采样器s在标量t位置的color4 | |
| tex1D(s,t,ddx,ddy) | 使用微分查询一维纹理t和ddxy均为vector | |
| tex1Dlod(s,t) | 使用LOD查找纹理s在t.w位置的color4 | |
| tex1Dbias(s,t) | 将t.w决定的某个MIP层偏置后的一维纹理查找 | |
| tex1Dgrad(s,t,ddx,ddy) | 使用微分并制定MIP层的一维纹理查找 | |
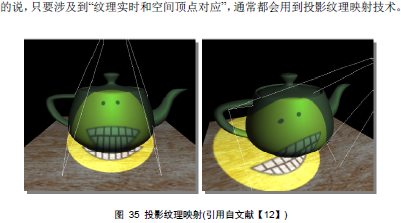
| tex1Dproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先试用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
|


9.2D纹理查找
| 函数 | 含义 | 示例图 |
| tex2D(s,t) | 普通二维纹理查找,返回纹理采样器s在vector t位置的颜色 | |
| tex2D(s,t,ddx,ddy) | 使用微分查询二维纹理 t和ddxy均为vector | |
| tex2Dlod(s,t) | 使用LOD查找纹理s在t.w位置的color4 |
|
| tex2Dbias(s,t) | 将t.w决定的某个MIP层偏置后的二维纹理查找 |
|
| tex2Dgrad(s,t,ddx,ddy) | 使用微分并指定MIP层的二维纹理查找 |
|
| tex2Dproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先使用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
10.3D纹理查找
| 函数 | 含义 | 示例图 |
| tex3D(s,t) | 普通三维纹理查找,返回纹理采样器s在vector t位置的颜色 |
|
| tex3D(s,t,ddx,ddy) | 使用微分查询三维纹理 t和ddxy均为vector | |
| tex3Dlod(s,t) | 使用LOD查找纹理s在t.w位置的color4 | |
| tex3Dbias(s,t) | 将t.w决定的某个MIP层偏置后的三维纹理查找 | |
| tex3Dgrad(s,t,ddx,ddy) | 使用微分并指定MIP层的三维纹理查找 | |
| tex3Dproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先使用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
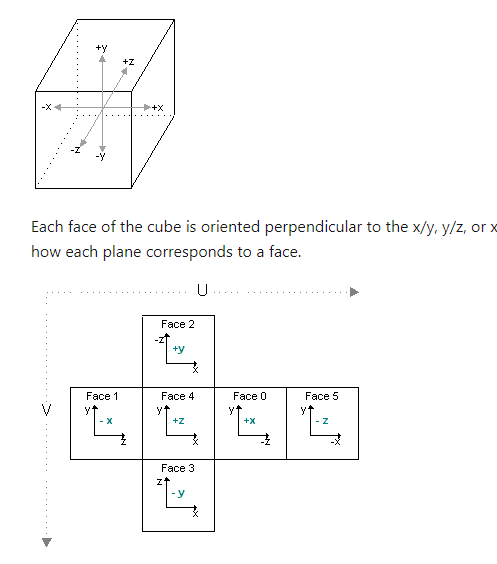
11.立体纹理查找
| 函数 | 含义 | 示例图 |
| texCUBE(s,t) | 返回纹理采样器s在vector t位置的颜色 |
|
| texCUBE(s,t,ddx,ddy) | 使用微分查询一维纹理t和ddxy均为vector | |
| texCUBElod(s,t) | 使用LOD查找纹理s在t.w位置的color4 | |
| texCUBEbias(s,t) | 将t.w决定的某个MIP层偏置后的一维纹理查找 | |
| texCUBEgrad(s,t,ddx,ddy) | 使用微分并制定MIP层的一维纹理查找 | |
| texCUBEproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先试用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
参考链接:
Cg(C for Graphic)语言标准函数库之纹理映射函数,偏导函数,与调试函数_liu_lin_xm的博客-CSDN博客
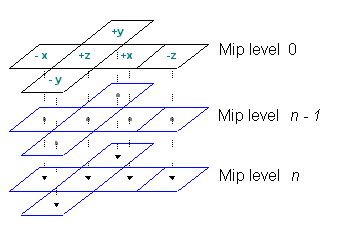
Mipmap:
MipMap的LOD实现原理_tex2dgrad_jieniyimiao的博客-CSDN博客
Unity中关于 Mipmap_mipmaps_u010019717的博客-CSDN博客
2D:
tex2Dbias
3D:
Introduction To Textures in Direct3D 11 - Win32 apps | Microsoft Learn
Texture Coordinates (Direct3D 9) - Win32 apps | Microsoft Learn
3D Textures
立体纹理查找:
Cubic Environment Mapping (Direct3D 9) - Win32 apps | Microsoft Learn
作业:
写出你觉得最常用的5个函数
- tex2D(s,t)
- normalize(x)
- saturate(x)
- dot(x,y)
- lerp(x,y,t)
ddx、ddy的实际使用测试
1.锐化图像
fixed4 frag (v2f i) : SV_Target
{
fixed4 col = tex2D(_MainTex, i.uv);
col += ddx(col * _DDXIntensity)+ ddy(col * _DDYIntensity);
return fixed4(col.rgb,1.0);
}右图为锐化intensity=1时

最后输出ddx(col * _DDXIntensity)+ ddy(col * _DDYIntensity)则可以看到锐化范围。

2.求面法线
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
float3 normal : TEXCOORD3;
};
struct v2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
float3 pos : TEXCOORD1;
float3 worldPos : TEXCOORD2;
float3 worldNormal : TEXCOORD3;
};
sampler2D _MainTex;
float4 _MainTex_ST;
float _Intensity;
float _DDXIntensity;
float _DDYIntensity;
v2f vert (appdata v)
{
v2f o;
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
o.vertex = UnityObjectToClipPos(v.vertex);
o.worldPos = mul(unity_ObjectToWorld,v.vertex).xyz;
o.worldNormal = mul(v.vertex,(float3x3)unity_WorldToObject).xyz;
return o;
}
fixed4 frag (v2f i) : SV_Target
{
fixed3 col = tex2D(_MainTex, i.uv);
//锐化
//col += ddx(col * _DDXIntensity)+ ddy(col * _DDYIntensity);
//求面法线
col = normalize(cross(ddy(i.worldPos),ddx(i.worldPos)));
return fixed4(col,1.0);
}