微信公众号:码云成化
关注可了解更多的教程及进阶技巧。问题或建议,请公众号留言;
如果你觉得阿云对你有所帮助,欢迎赞赏
深度的定义
[ 当前结点的层数。默认叶子节点是 null 节点,深度是 0 。其子节点是 null 节点,深度是 1 。 ]
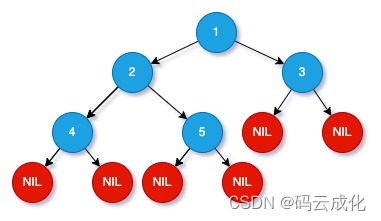
- 给出上图一个普通二叉树,如果计算结点深度,用我们大脑去做的话会怎么做呢?我觉得一般人思路应该是这样的,先把最直观的信息采集起来。
- 那么 [4] 结点的深度、[5] 结点的深度、[3] 结点的深度,因为它们都没有子节点,深度都是 1 。
- 根据 [4] 结点的深度和 [5] 结点的深度,可以求出 [2] 结点的深度,max( [4] 结点的深度, [5] 结点的深度 ) + 1 = 2。
- 有了 [2] 结点的深度和 [3] 结点的深度,可以求出 [1] 结点的深度,max( [2] 结点的深度, [3] 结点的深度 ) + 1 = 3。
深度优先搜索
大多数使用的是递归函数。其实并没有名字所说的那么复杂,使用递归函数对整个目标进行遍历。
递归函数的三要素
- 子问题与原问题做同样的事。
- 需要有一个要递归函数结束的出口。
- 递归表达式。
递归过程
- 求 depth( [1] 结点 ) 必求 depth( [2] 结点 ) 和 depth( [3] 结点 )
- 求 depth( [2] 结点 ) 必求 depth( [4] 结点 ) 和 depth( [5] 结点 )
递归表达式
depth(rt)=max(depth(rt->left), depth(rt->right))+1;
编程实现
package com.pure.common.recursion;
/**
* @desc: 二叉树深度遍历
**/
public class DepthUtil {
// 结点类
public static class TreeNode {
private int node;
private TreeNode left;
private TreeNode right;
public TreeNode() {
}
public TreeNode(int node) {
this.node = node;
}
public int getNode() {
return node;
}
public void setNode(int node) {
this.node = node;
}
public TreeNode getLeft() {
return left;
}
public void setLeft(TreeNode left) {
this.left = left;
}
public TreeNode getRight() {
return right;
}
public void setRight(TreeNode right) {
this.right = right;
}
@Override
public String toString() {
return "TreeNode{" +
"node=" + node +
", left=" + left +
", right=" + right +
'}';
}
}
public static void main(String[] args) {
TreeNode root$1 = new TreeNode(1);
TreeNode node$2 = new TreeNode(2);
TreeNode node$3 = new TreeNode(3);
TreeNode node$4 = new TreeNode(4);
TreeNode node$5 = new TreeNode(5);
// 1 结点
root$1.setLeft(node$2);
root$1.setRight(node$3);
// 2 结点
node$2.setLeft(node$4);
node$2.setRight(node$5);
System.out.println("root 结点深度是:" + depth(root$1));
System.out.println("node$2 结点深度是:" + depth(node$2));
System.out.println("node$3 结点深度是:" + depth(node$3));
System.out.println("node$4 结点深度是:" + depth(node$4));
System.out.println("node$5 结点深度是:" + depth(node$5));
}
// 深度递归函数
public static int depth(TreeNode root) {
if (null == root) {
return 0;
}
int l, r;
l = depth(root.getLeft());
r = depth(root.getRight());
return Math.max(l, r) + 1;
}
}
输出结果
root 结点深度是:3
node$2 结点深度是:2
node$3 结点深度是:1
node$4 结点深度是:1
node$5 结点深度是:
希望可以帮到你!相互取暖,共同进步。