题目

Ural大学有N名职员，编号为1~N。
他们的关系就像—棵以校长为根的树，父节点就是子节点的直接上司。每个职员有一个快乐指数，用整数H给出，其中1≤i≤N。
现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。
在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式

第一行一个整数N。
接下来N行，第i行表示i号职员的快乐指数H;。
接下来N-1行，每行输入—对整数L,K,表示K是L的直接上司。最后一行输入0,0。

输出格式

输出最大的快乐指数。

数据范围

1<N<6000,—128<Hi≤127

• 输入样例:

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
0 0

• 输出样例:

5

题解

import java.util.Arrays;
import java.util.Scanner;

/**
 * @author akuya
 * @create 2023-07-28-21:52
 */
public class ball {
    static int N=6010;
    static int n;
    static int happy[]=new int[N];
    static int h[]=new int[N];
    static int e[]=new int[N];
    static int ne[]=new int[N];
    static int idx;
    static int f[][]=new int[N][2];
    static boolean has_father[]=new boolean[N];

    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        for(int i=1;i<=n;i++)happy[i]=scanner.nextInt();

        Arrays.fill(h,-1);
        for(int i=0;i<n-1;i++){
            int a,b;
            a=scanner.nextInt();
            b=scanner.nextInt();
            has_father[a]=true;
            add(b,a);
        }

        int root=1;
        while(has_father[root])root++;
        dfs(root);
        System.out.println(Math.max(f[root][0],f[root][1]));
    }

    public static void add(int a,int b){
        e[idx]=b; ne[idx]=h[a];h[a]=idx++;
    }

    public static void dfs(int u){
        f[u][1]=happy[u];
        for(int i=h[u];i!=-1;i=ne[i]){
            int j=e[i];
            dfs(j);

            f[u][0]+=Math.max(f[j][0],f[j][1]);
            f[u][1]+=f[j][0];
        }
    }
}

思路

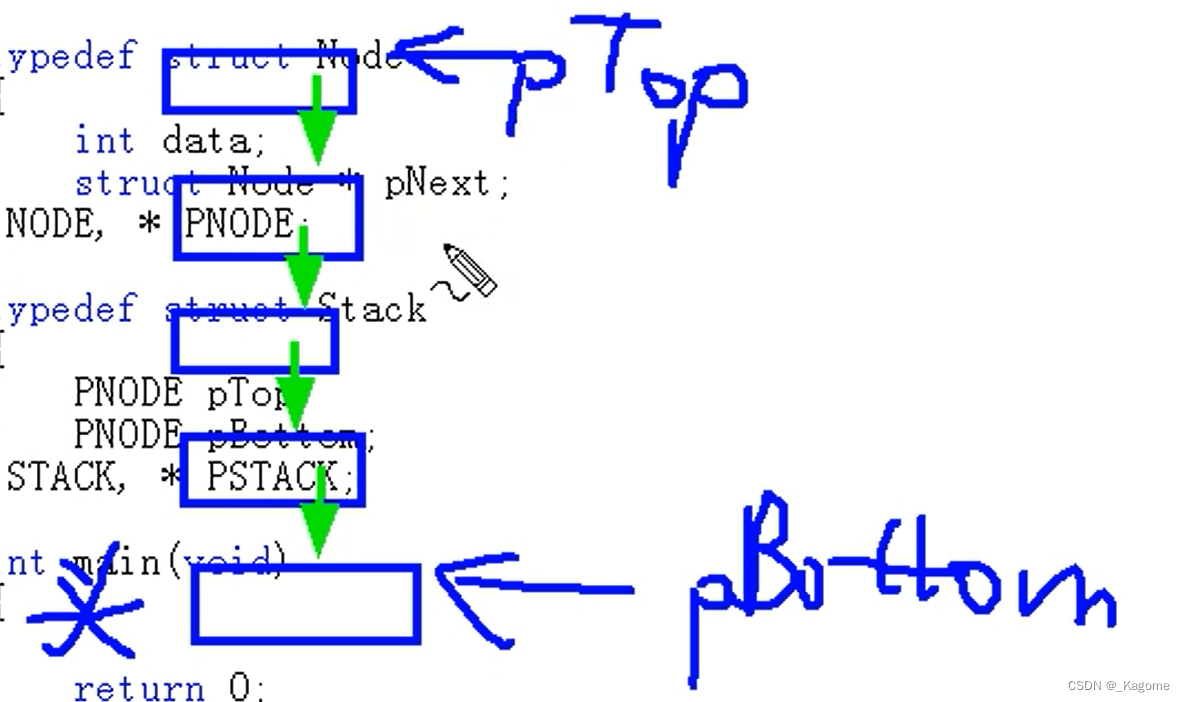
本题为树形动态规划，思路如下图


动态转移方程如上图，结合之前学习的静态链表即可完成。