算法与数据结构31:DC3算法生成后缀数组
- 什么是后缀数组
- 引出DC3算法
- DC3算法具体实现
- DC3算法模板
- DC3模板的用法
- 一个可以使用DC3的题
什么是后缀数组
假设有字符串 aabaabaa
那么从每个位置开始,到结尾位置,截取后缀串,可得
a
aa
baa
abaa
aabaa
baabaa
abaabaa
aabaabaa
然后根据字典序对后缀串进行排序,排序结果放入数组中,数组中的值表示后缀串的开头位置
[7,6,3,0,4,1,5,2]
那么这个数组,就是后缀数组




对一个字符串求后缀数组,求实就是对一个数组求后缀数组,因为字符串里面每个字符都对应衣蛾ASCII码,也就是一个ASCII码数组
假设有数组
[103, 56, 27, 103]
那么后缀串就是
103
27 103
56 27 103
103 56 27 103
后缀数组就是
[2, 1, 3, 0]
生成后缀串,是枚举每个开始位置,然后往后截取,这个动作就是O(N^2)
那么对这N个后缀串排序,就是O(N * logN),而字符串比较本身又不是O(1),所以其实排序还不止O(N * logN),应该是O(N * logN * N)
这个时间复杂度是很高的
那么有没有更好的方式生成后缀数组呢?
引出DC3算法
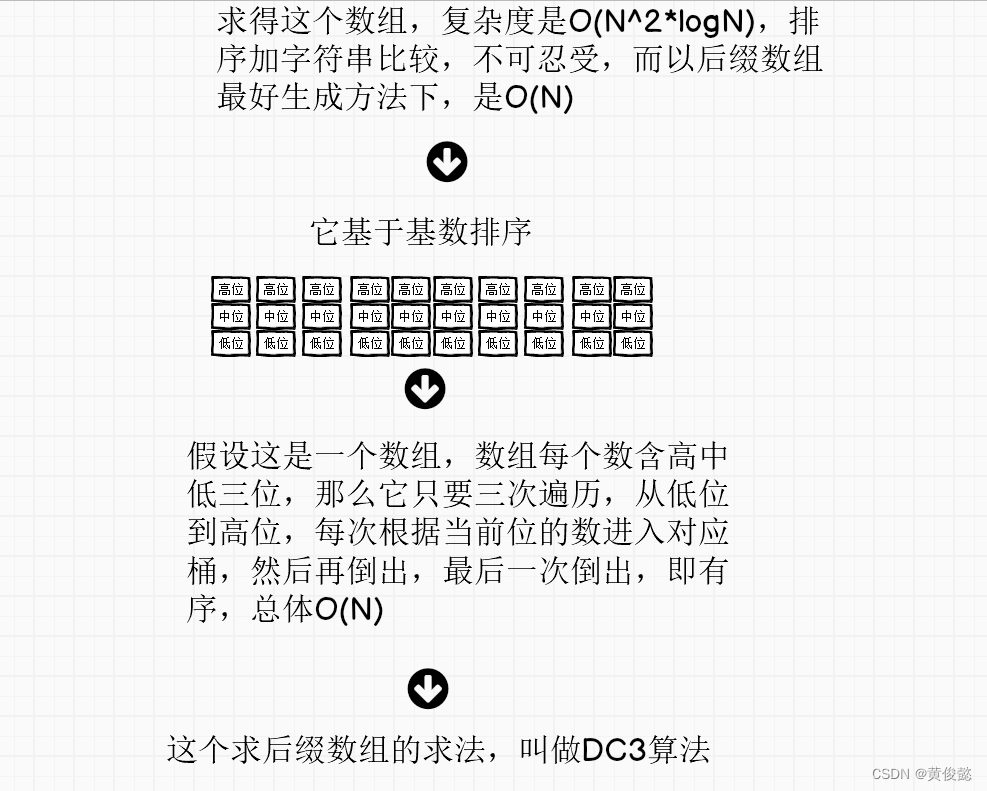
假设有N个样本,N很大
而样本有3维数据,这些数据都不大(比如小于10)
比如
A样本: 13 27 09
B样本: 26 13 100
C样本: 21 19 56
如果要根据样本的3维数据排序,一维数据谁小谁排前面,一维一样看二维数据,谁小谁排前面,二维数据一样,看三维数据,谁小谁排前面
这个用什么排序算法最快呢?基数排序
每个样本,先根据第三维数据决定进几号桶
然后从桶中倒出来后,就根据第三维数据排好序了
然后再根据第二维数据决定进几号桶…
然后再根据第一维数据进几号桶…
最后倒出来,就是最终排好序的顺序
因为只有三维数组,在每个维度都比较小的情况下,复杂度是O(N)的
DC3算法具体实现
1、先按下标%3进行分类,下标%3后是几,就是第几类:

2、假设有一个方法,可以把很方便的把s1和s2两类后缀串进行排序

3、那么s1和s2排好序后,能否更加s1和s2的排序信息,得出s0类后缀串的排序呢?

这个a3,a1,就是两维数据
第一维是自己的字符,第二维是除自己字符外,剩下的后缀串的排名

这样就得出了s0类后缀串的排序了
4、归并排序,合并s0和s1/s2的排序

具体比法:
s0和s2类后缀串比较,比三维数据,前两维比字符,第三维比s1/s2排名,
因为第三维数据两边都是s1或s2,就可以比排名了
s0和s1类后缀串比较,比二维数据,第一维比字符,第二维比s1/s2排名
也就是说如果当前维度的数据,左右下标有一个在s0里,则比较用字符
如果左右两边下标都不在s0里,那么这一维就用s1/s2排名比较
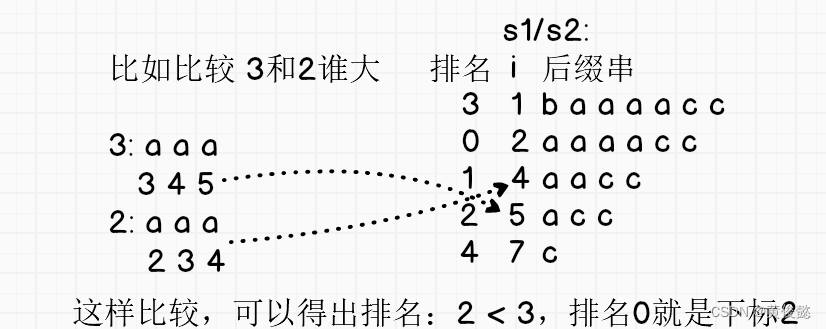
5、那如何得出s1、s2的排名呢?而且排名是精确的,不能有重复。
先每个位置都拿前3个字符,然后进行比较
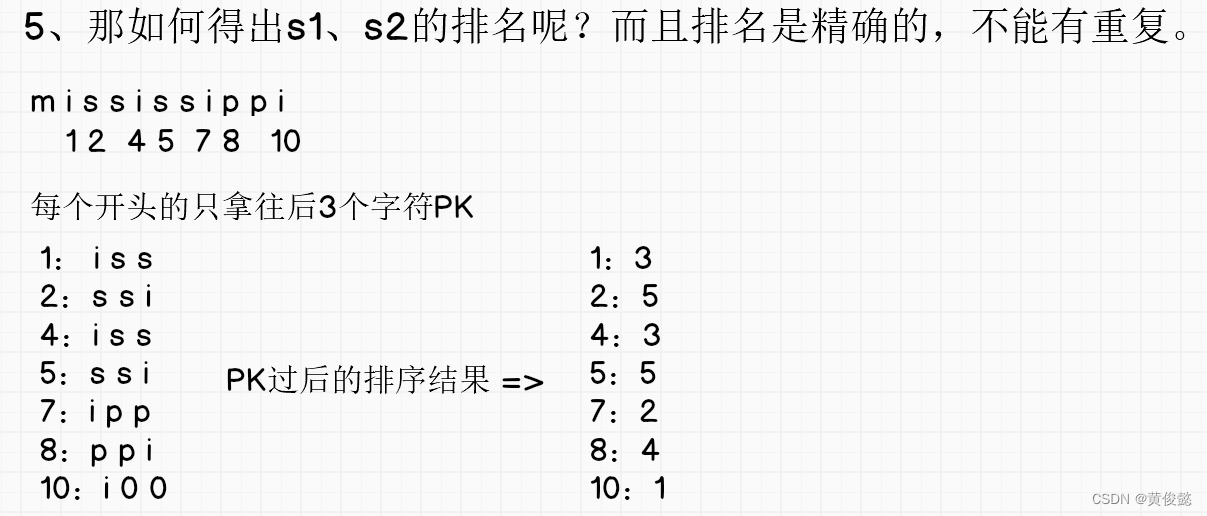
但是因为有重复的元素,所以排序有重复
因此还要进行递归处理
s1类放左边,s2类放右边,把排名放进去,组成一个字符串,递归求后缀数组,得出一个新排名



总结:
1、以方便的方法,得出s1/s2下标的排名
2、根据s1/s2的排名,得出s0的排名
3、合并so和s1/s2的排名,得出后缀数组
注意:因为用到了基数排序,所以必须保证数组中每个数都不会太大
DC3算法模板
public class DC3 {
public int[] sa;
public int[] rank;
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i + 1;
}
return ans;
}
}
DC3模板的用法
要对哪个数组求后缀数组,就把该数组最为构造函数的nums参数传入
字符串要先转型整形数组
数组中最小值,要大于等于1,如果不满足这个条件,就要处理一下
构造函数的第二个参数max,就是数组中的最大值
sa数组下标是排名,下标对应的值是这个排名对应的在原数组中的位置
sa[i] 第i名的是哪个位置开头的
rank数组下标就是原数组中的位置,值就是这个位置对应的排名
rank[i] 以i位置开头的时第几名
一个可以使用DC3的题
给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数,要求从同一个数组中取出的数字保持其在原数组中的相对顺序。
求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。
说明: 请尽可能地优化你算法的时间和空间复杂度。
示例 1:
输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]
示例 2:
输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:
[6, 7, 6, 0, 4]
示例 3:
输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:
[9, 8, 9]
/**
*
* 给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数,要求从同一个数组中取出的数字保持其在原数组中的相对顺序。
* 求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。
* 说明: 请尽可能地优化你算法的时间和空间复杂度。
*
* 示例 1:
* 输入:
* nums1 = [3, 4, 6, 5]
* nums2 = [9, 1, 2, 5, 8, 3]
* k = 5
* 输出:
* [9, 8, 6, 5, 3]
*
* 示例 2:
* 输入:
* nums1 = [6, 7]
* nums2 = [6, 0, 4]
* k = 5
* 输出:
* [6, 7, 6, 0, 4]
*
* 示例 3:
* 输入:
* nums1 = [3, 9]
* nums2 = [8, 9]
* k = 3
* 输出:
* [9, 8, 9]
*
* Created by huangjunyi on 2022/10/22.
*/
public class CreateMaximumNumber {
public static int[] maxNumber(int[] nums1, int[] nums2, int k) {
int N1 = nums1.length;
int N2 = nums2.length;
if (k < 0 || k > N1 + N2) return null;
/*
思路:
比如k是5,那就是从num1和num2中挑5个数组成最大值
那么就枚举
num1挑5个,num2挑0,组成的最大值
num1挑4个,num2挑1,组成的最大值
num1挑3个,num2挑2,组成的最大值
num1挑2个,num2挑3,组成的最大值
num1挑1个,num2挑4,组成的最大值
num1挑0个,num2挑5,组成的最大值
这些最大值中挑最大
生成一个N*N+1的dp1和dp2表,方便快速挑数
dp[i][j]表示从i往后挑,挑j个数,挑出的时最大的方案,挑出的开头的数的下标
那么比如要从num1中挑3个
第一个数取dp[0][3],假如得出是2,表示开头为下标2的数
第二个数取dp[3][2],假如得出是4,表示第二个数是下标为4的数
第三个数取dp[5][1]
然后从num1和num2挑出分表挑出2个数组后,就根据进行合并,
合并规则是保证原数组中的顺序下,组成的数是最大
正常的合并方法:
[3,3,3,9]
[3,3,3,2]
合并后:[3,3,3,9,3,3,3,2]
为了让9尽快出现,需要把第一个数组的3尽快刷完
所以每次都两个指针分别PK,一样就同时后移,直到分出胜负,取胜方的为取出的第一个数
比如第一轮比较:大家都是前面3个3,直到第四个数,9比2大,去第一个数组的3
后面每次比较,都会遍历到9时第一个数组胜出,所以第一个数组会顺利的有序被刷完
但是这个合并方式不是最优方案
优化后的合并的方式,是通过后缀数组合并,在后缀数组中排名越大的,合并后越靠前
因为后缀数组得出的排序结果,可以告诉我们两个下标PK谁赢
*/
int[] res = new int[k];
int[][] dp1 = getdp(nums1);
int[][] dp2 = getdp(nums2);
// 这里要处理边界条件,因为nums1或者nums2可能不够k个数
for (int get1 = Math.max(0, k - N2); get1 <= Math.min(k, N1); get1++) {
int[] pick1 = maxPick(nums1, dp1, get1);
int[] pick2 = maxPick(nums2, dp2, k - get1);
int[] merge = mergeBySuffixArray(pick1, pick2);
res = moreThan(res, merge) ? res : merge;
}
return res;
}
/**
* 比较两个方案哪个更大
* @param pre
* @param last
* @return
*/
public static boolean moreThan(int[] pre, int[] last) {
int i = 0;
int j = 0;
while (i < pre.length && j < last.length && pre[i] == last[j]) {
i++;
j++;
}
return j == last.length || (i < pre.length && pre[i] > last[j]);
}
/**
* 通过后缀数组进行merge
* @param nums1
* @param nums2
* @return
*/
public static int[] mergeBySuffixArray(int[] nums1, int[] nums2) {
int size1 = nums1.length;
int size2 = nums2.length;
int[] nums = new int[size1 + 1 + size2];
for (int i = 0; i < size1; i++) {
// 因为两个数组中间放了个1做隔断,所以每个数都加2,保证隔断比其他的数都小(0 + 2 都 比 1 大)
nums[i] = nums1[i] + 2;
}
// 两个数组中间放一个1做隔断,本来放0,但是0会被用于在生成后缀数组时做边界处理,所以用1
nums[size1] = 1;
for (int j = 0; j < size2; j++) {
// 因为两个数组中间放了个1做隔断,所以每个数都加2,保证隔断比其他的数都小(0 + 2 都 比 1 大)
nums[j + size1 + 1] = nums2[j] + 2;
}
// 通过DC3模板生成后缀数组
DC3 dc3 = new DC3(nums, 11);
int[] rank = dc3.rank;
int[] ans = new int[size1 + size2];
int i = 0;
int j = 0;
int r = 0;
// 在后缀数组中排名越大的,合并后越靠前
while (i < size1 && j < size2) {
ans[r++] = rank[i] > rank[j + size1 + 1] ? nums1[i++] : nums2[j++];
}
while (i < size1) {
ans[r++] = nums1[i++];
}
while (j < size2) {
ans[r++] = nums2[j++];
}
return ans;
}
/**
* 生成用于加速挑数的dp表
* dp[i][j]:
* 如果arr[i] > arr[dp[i + 1][j]],dp[i][j] = i;
* 如果arr[i] < arr[dp[i + 1][j]],dp[i][j] = dp[i + 1][j];
* 如果arr[i] == arr[dp[i + 1][j]],dp[i][j] = i;
* 相等填i,是因为这里有个小贪心,选了i,后面还能多拿一个和i一样的数,否则挑出的也就是dp[i+1][j]对应的方案,就不是最右方案
* @param arr
* @return
*/
public static int[][] getdp(int[] arr) {
int size = arr.length; // 0~N-1
int pick = arr.length + 1; // 1 ~ N
int[][] dp = new int[size][pick];
// get 不从0开始,因为拿0个无意义
// get 1
for (int get = 1; get < pick; get++) { // 1 ~ N
int maxIndex = size - get;
// i~N-1
for (int i = size - get; i >= 0; i--) {
if (arr[i] >= arr[maxIndex]) {
maxIndex = i;
}
dp[i][get] = maxIndex;
}
}
return dp;
}
/**
* 从arr中挑选pick个数组成的最优结果,利用dp加速
* @param arr
* @param dp
* @param pick
* @return
*/
public static int[] maxPick(int[] arr, int[][] dp, int pick) {
int[] res = new int[pick];
for (int resIndex = 0, dpRow = 0; pick > 0; pick--, resIndex++) {
res[resIndex] = arr[dp[dpRow][pick]];
dpRow = dp[dpRow][pick] + 1;
}
return res;
}
}