A - AtCoder Quiz 3A - AtCoder Quiz 3
题目大意
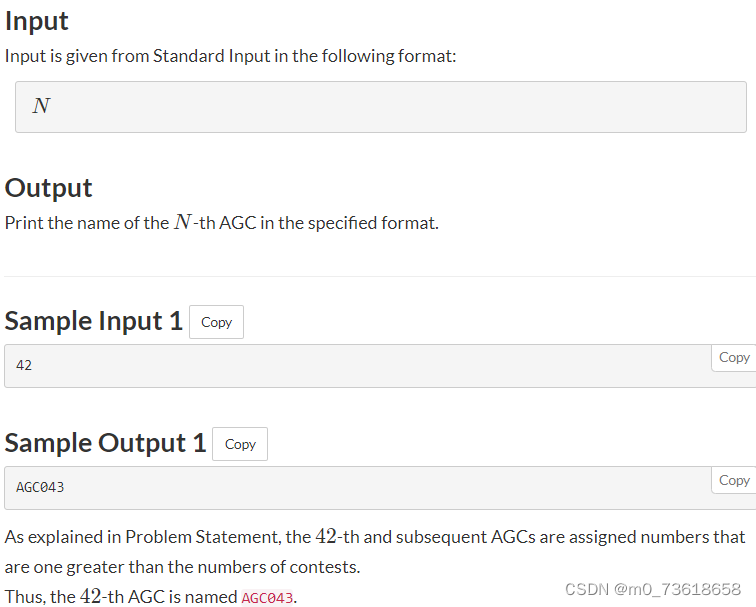
给定一个整数N,以AGCXXX的格式打印第N次AGC的名称,其中XXX是以零填充的3位数字。
思路分析
根据题目要求,当N≥42时,输出AGC加上N+1,并补齐为3位数字的格式;否则,输出AGC加上N,并补齐为3位数字的格式。
时间复杂度
O(1)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int x;
cin>>x;
if(x>=42) cout<<"AGC"<<setw(3)<<setfill('0')<<x+1<<'\n';
else cout<<"AGC"<<setw(3)<<setfill('0')<<x<<'\n';
return 0;
}
B - Triple MetreB - Triple Metre
题目大意
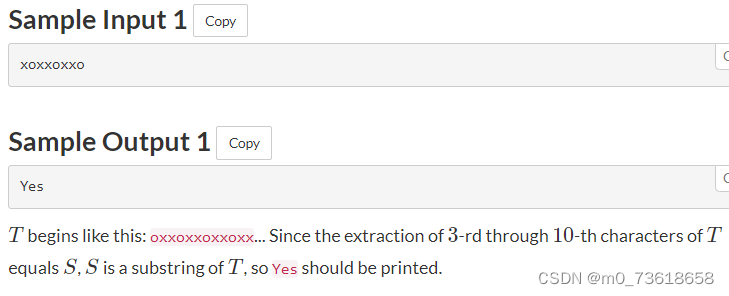
给定一个字符串S,判断S是否为字符串T的子串。当存在一对整数i和j(1≤i≤j≤∣T∣)满足条件:从T中提取第i到第j个字符而不改变顺序后,得到的字符串与S相等时,称S为T的子串。令TT为oxx的105个拼接而成的字符串。给定一个字符串S,如果S是T的子串,则输出Yes,否则输出No。
思路分析
可以构造一个字符串TT,将’oxx’重复拼接105次。然后使用字符串的find函数来判断S是否是T的子串。如果find函数返回的值不等于string::npos,就说明S是T的子串。
时间复杂度
O(k * 105)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
string t;
cin >> t;
string s = "oxx";
string TT = "";
for(int i=0; i<100000; i++) {
TT += s;
}
if(TT.find(t) != string::npos) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
}
return 0;
}
C - X drawingC - X drawing
题目大意
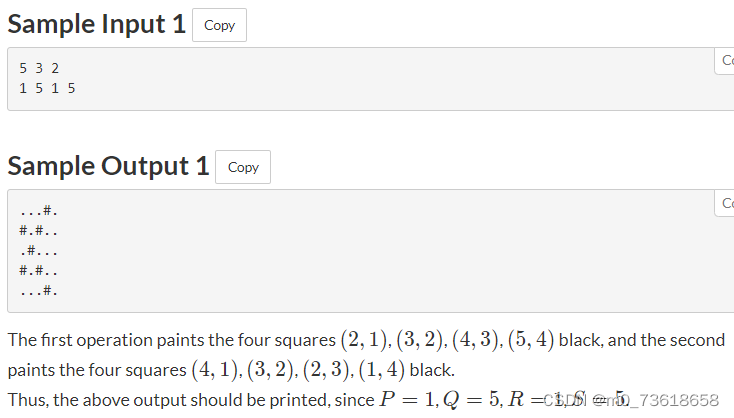
要求在一个N×N的网格上进行操作,初始状态所有方格都是白色。每次操作有两个步骤:根据给定的参数A和B,将一些方格涂成黑色。
- 第一次操作:对于满足max(1−A,1−B)≤k≤min(N−A,N−B)的整数k,将方格(A+k,B+k)涂成黑色。
- 第二次操作:对于满足max(1−A,B−N)≤k≤min(N−A,B−1)的整数k,将方格(A+k,B−k)涂成黑色。
思路分析
可以通过模拟操作来确定每个方格的颜色。
首先,可以使用一个二维数组来表示网格,数组的元素可以是字符类型,用’.‘表示白色,用’#'表示黑色。
然后,根据操作规则,我们可以用两个循环分别处理两种操作:
- 对于第一种操作,遍历满足条件的k,将网格中的对应方格(A+k,B+k)设为黑色。
- 对于第二种操作,遍历满足条件的k,将网格中的对应方格(A+k,B-k)设为黑色。
最后,根据给定的范围P、Q、R、S,输出网格中对应范围内的方格颜色。
时间复杂度
O(N + (Q-P+1)×(S-R+1))
AC代码
#include <bits/stdc++.h>
using namespace std;
int main(void) {
long long n, a, b;
long long p, q, r, s;
long long x, y;
string str = "";
vector<string> ans;
cin >> n >> a >> b;
cin >> p >> q >> r >> s;
for (long long i = 0; i < (s - r + 1); i++) {
str += '.';
}
for (long long i = 0; i < (q - p + 1); i++) {
ans.push_back(str);
}
x = max(p - a, r - b);
y = min(q - a, s - b);
for (long long i = x; i <= y; i++) {
ans[a + i - p][b + i - r] = '#';
}
x = max(p - a, b - s);
y = min(q - a, b - r);
for (long long i = x; i <= y; i++) {
ans[a + i - p][b - i - r] = '#';
}
for (long long i = 0; i < (q - p + 1); i++) {
cout << ans[i] << endl;
}
return 0;
}