目录

题目：

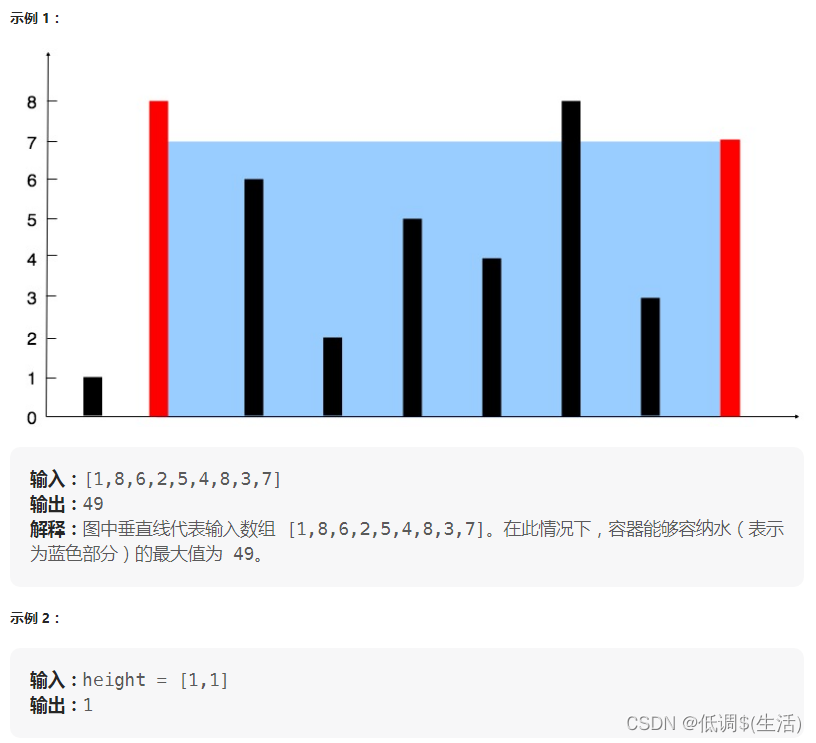
示例：

分析：

代码：

---

题目：

示例：

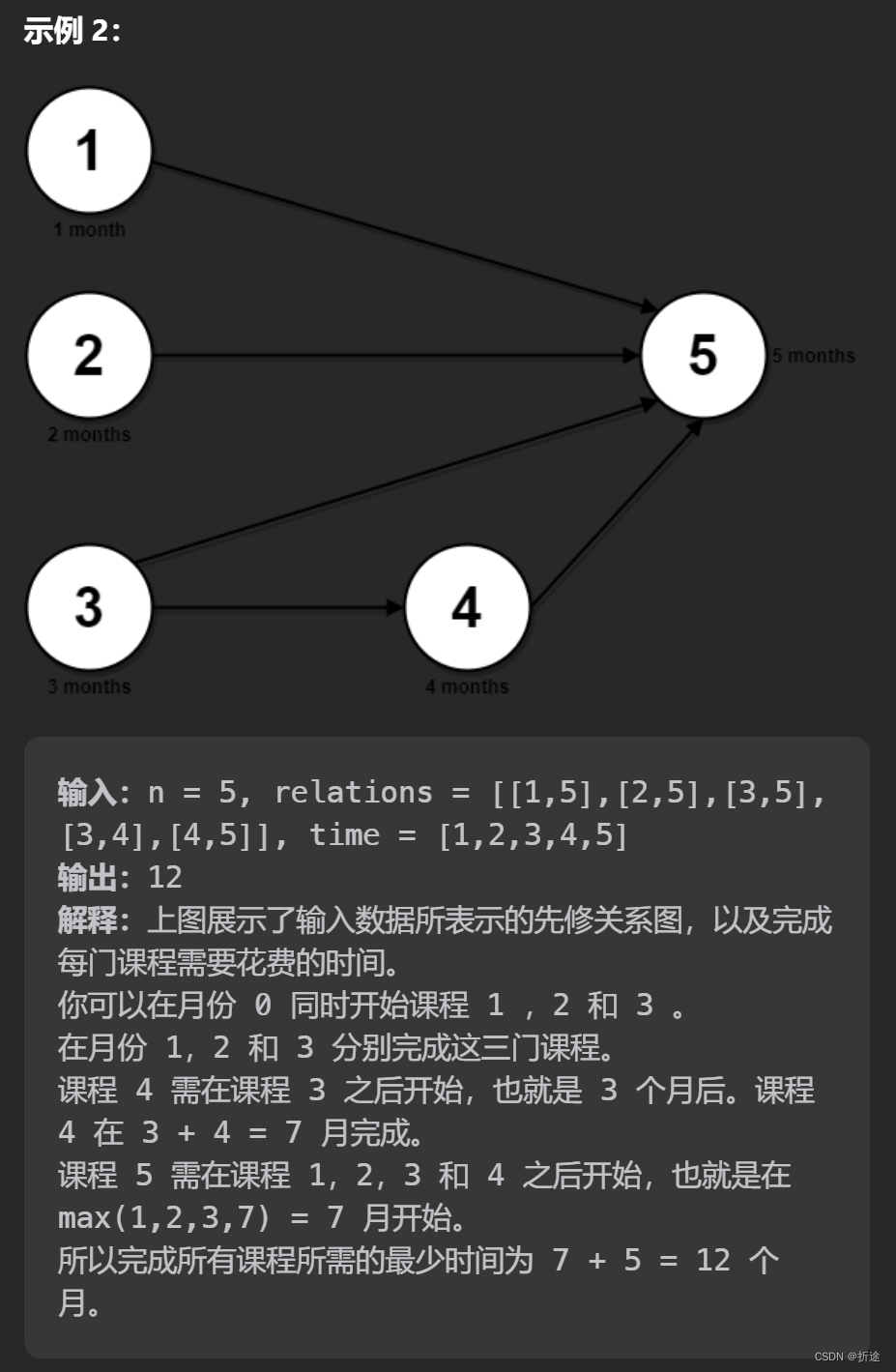
分析：

题目给我们课程表以及每门课需要学习的时间，我们可以同时学任意数量的课程，但是学习的条件是先修课程都已经学完了。问我们学习完所有课程需要花费的最少时间。

这是很典型的图论里的拓扑排序题，是有一套固定模板的，那么接下来我来一步一步介绍一下解题思路。

那么一般图论的题，我们都需要把图给构造出来，一般情况是可以用map来构造的，不过本题中作为map的键是课程号，而课程号是连续的，因此我们可以用vector来代替。构造图的过程就是遍历一边课程的关系，然后在先修课程的位置加上以此为先修课程的课程。

如果我们要学习一门课程，那么条件是先修课程已经修完了，我们可以理解成要学习一门课程的条件是未学习的先修课程数目为0。

因此我们需要另外定义一个数组来记录每门课程的先修数目，在遍历课程关系的时候可以顺便就记录下。

因为一开始就会有课程是没有先修课程的，是可以直接学习的，因此我们要初始化遍历一遍记录先修课程数目的vector，找到先修课程数目为0的课程，我们就将其放入待学队列。

然后开始while循环，条件是待学队列为空，因为题目有保证不会出现环，因此不会当待学队列为空的时候，就代表着所有课程已经学完。

每次我们从待学队列里拿出一个科目，然后开始遍历之前构造的图，把以本课程为先修课程的课程（后修课程）的先修课程数目减一，如果减到了0，那么将其送入待学队列。

我们另外需要一个数组来记录学习每个科目所需的最少时间。因为要学习一个课程，最少（没有先修课程的情况）需要花费学习自身的时间。所以在将课程从待学队列取出的时候，先在记录时间的数组里本课程的对应位置先加上学习自身的时间。

在遍历以后修课程时，把两门课所需花费的最少时间里取最大值赋给后修课程，因为我们是可以同时学多门课程的，因此学习某课程的先修课程的时间是取同一阶段的一个先修课程花费时间的最大值的，因为通过待学队列遍历的课程，我们都会加上本课程的学习时间，因此在循环别的课程的时候可以先忽略掉学习自身花费的时间。

当我们不在把课程送入待学队列后，直到待学队列为空，则表示我们以学完了所有课程，这时候我们从记录的学完每门课程的时间的数组里找出最大值，那就是我们修完所有课程所需要的最少时间了。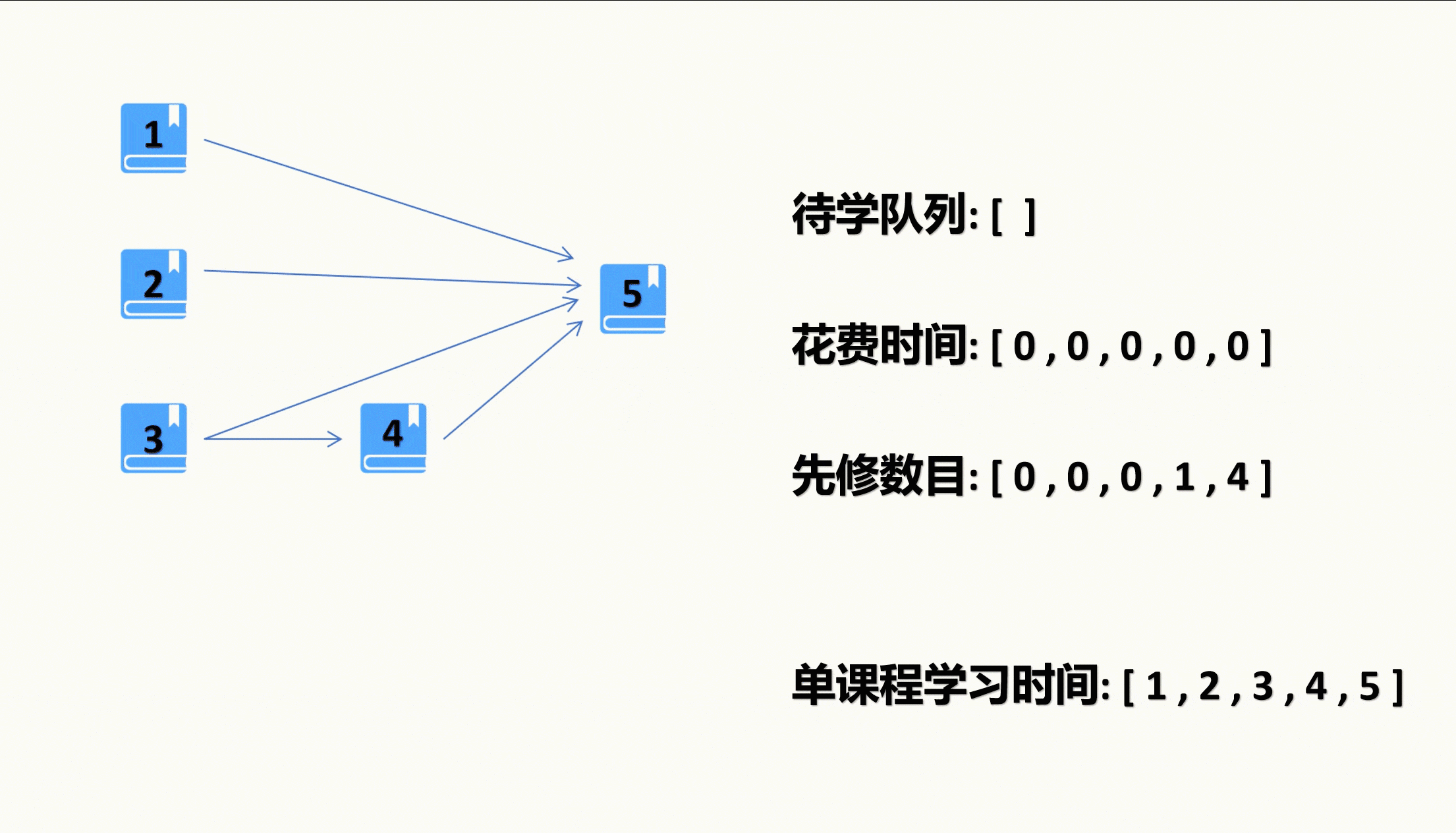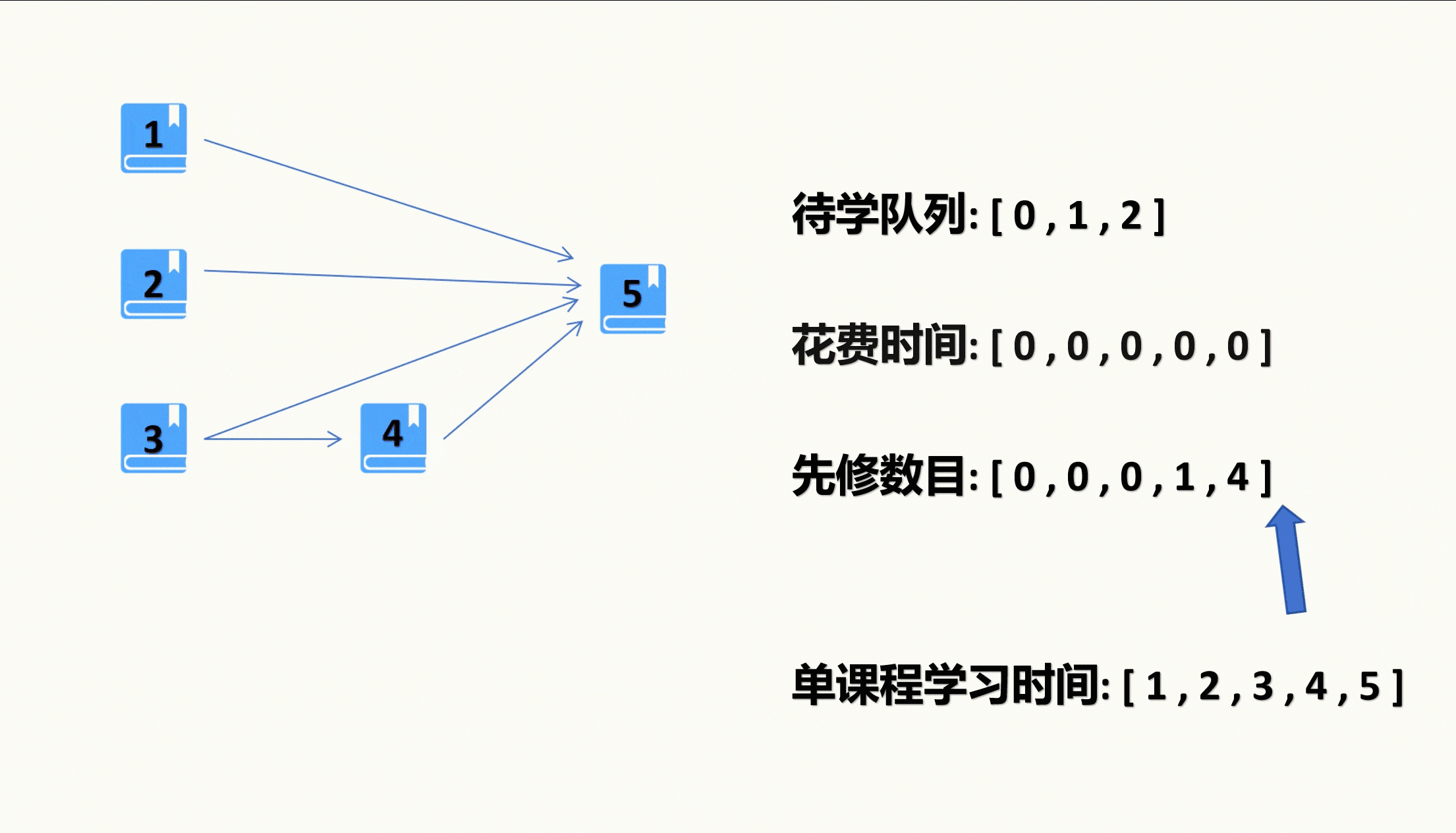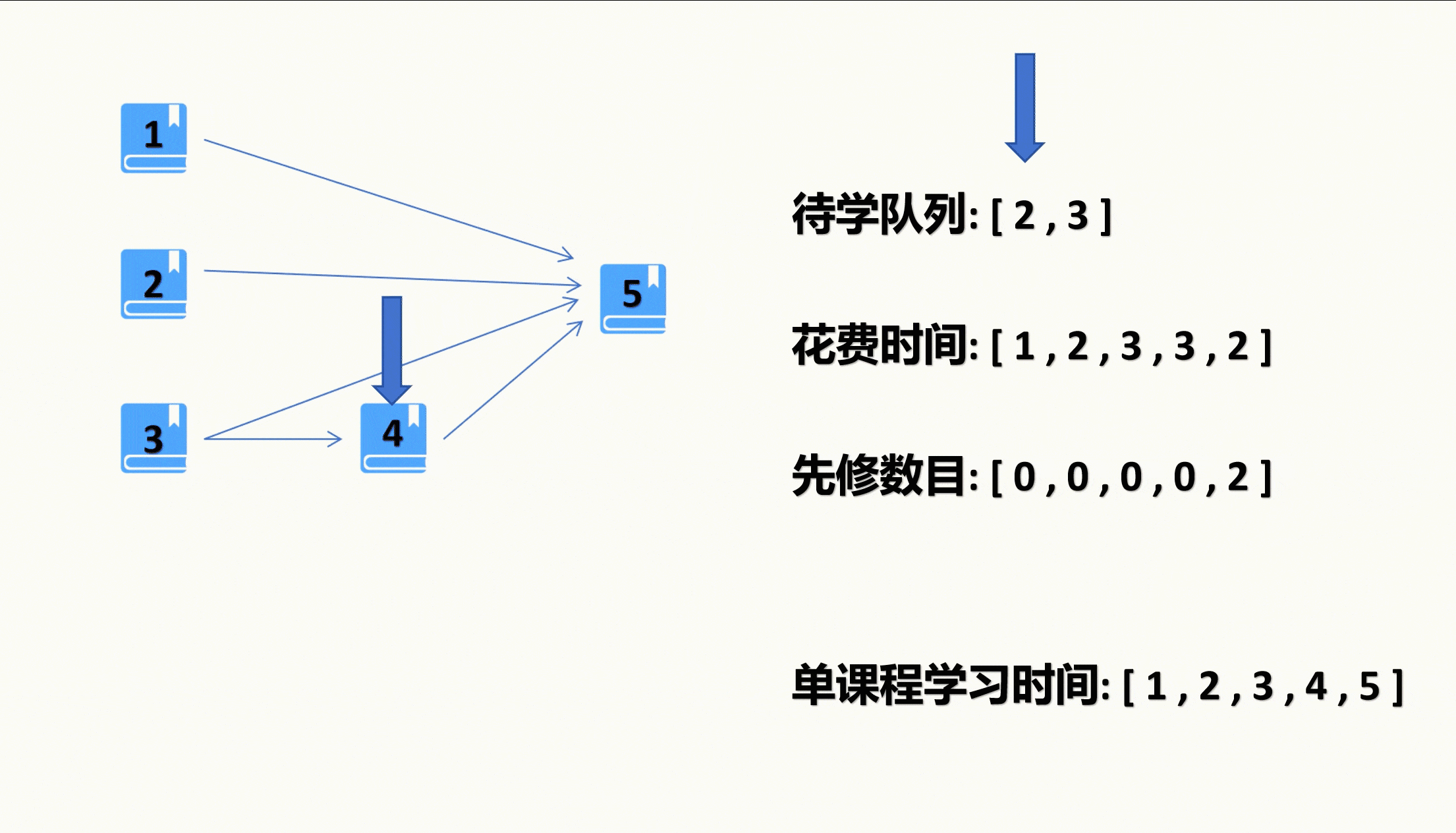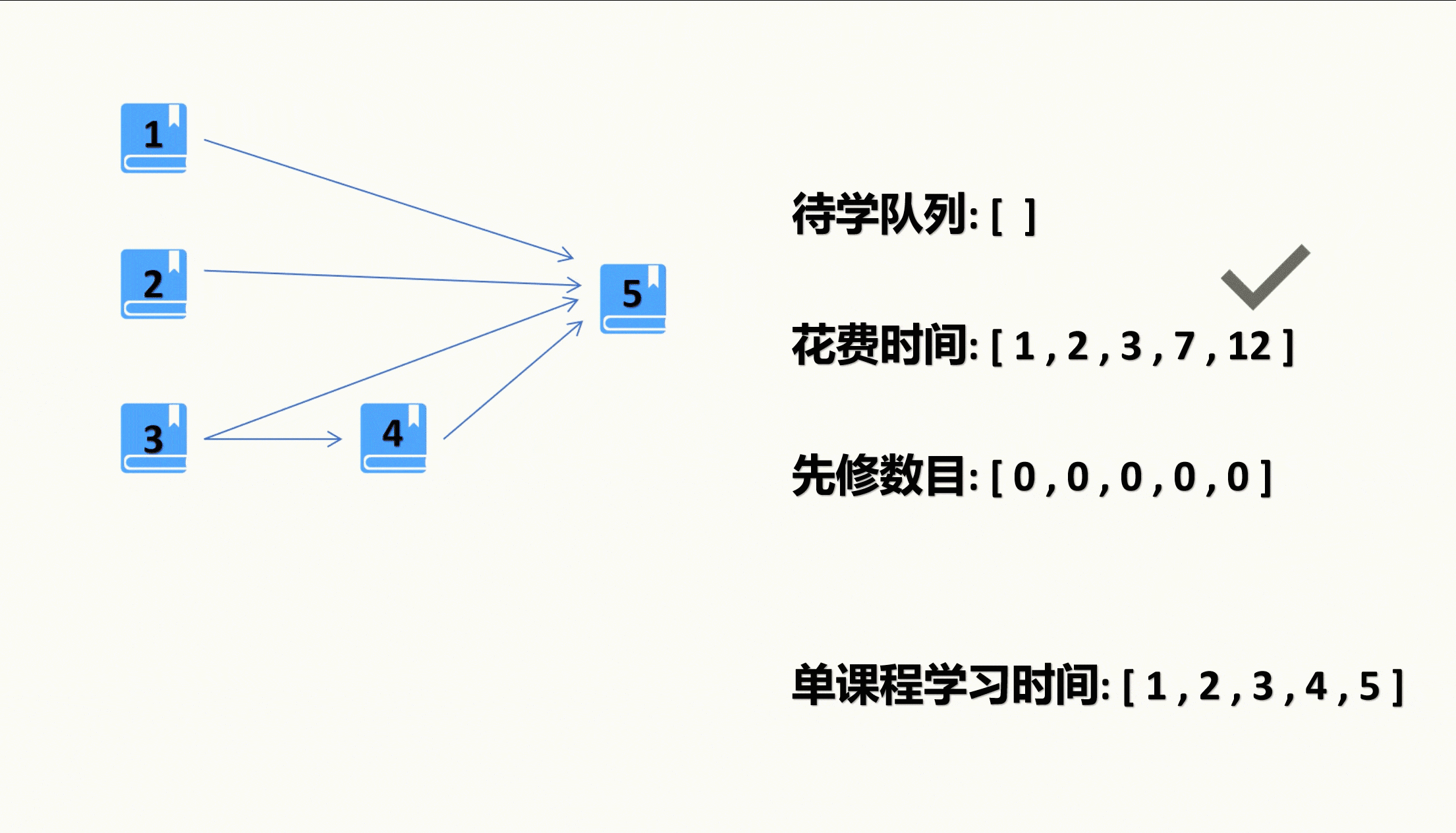

 

代码：

class Solution {
public:
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        vector<vector<int>>tu(n);   //图
        vector<int>much(n); //多少先修课
        queue<int>q;    //待学队列
        vector<int>least(n);    //每门课至少需要花费多少月
        for(auto& relation:relations){
            tu[relation[0]-1].push_back(relation[1]-1); //建立图
            much[relation[1]-1]++;  //获取先修课数量
        }
        for(int i=0;i<n;i++){
            if(much[i]==0){ //如果没有先修课,那么可以学,将其放入队列.
                q.push(i);
            }
        }
        while(!q.empty()){
            int temp=q.front();
            q.pop();
            least[temp]+=time[temp];    //学完这课程至少需要要学习本课的时间(先不算先修课)
            for(const auto& i:tu[temp]){   //遍历以本课作为先修课的课程
                //学习课程至少需要花费学习此时课程的时间(先不算自己的学习时间,以后遍历的时候会加上) 
                least[i]=max(least[i],least[temp]); 
                //把将本课程作为先修课的课程的先修课数目减少,如果减到0则表示下一轮可以学,入队
                if(--much[i]==0) q.push(i);     
            }
        }
        int res=0;
        for(const auto& i:least){
            res=max(res,i);
        }
        return res;
    }
};