字典树Trie

news2024/11/18 5:58:20

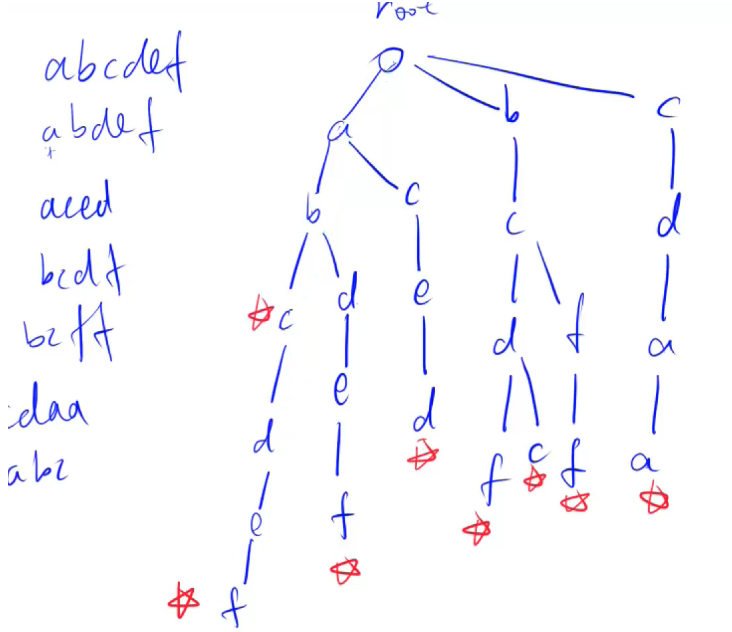
Trie树又称字典树，前缀树。是一种可以高效查询前缀字符串的树，典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。`做题看到大量字符串或者大量字符就往Trie树或者哈希这边想，因为速度很快.

image.png

AcWing 835. Trie字符串统计

https://www.acwing.com/activity/content/problem/content/883/

维护一个字符串集合，支持两种操作：

  1. I x 向集合中插入一个字符串 x x x；
  2. Q x 询问一个字符串在集合中出现了多少次。

共有 N N N 个操作，所有输入的字符串总长度不超过 1 0 5 10^5 105，字符串仅包含小写英文字母。

输入格式

第一行包含整数 N N N，表示操作数。

接下来 N N N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x x x 在集合中出现的次数。

每个结果占一行。

数据范围

1 ≤ N ≤ 2 ∗ 1 0 4 1 \le N \le 2*10^4 1≤N≤2∗104

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

思路

Trie树模版题

代码

/**
 * https://www.acwing.com/problem/content/837/
 */
#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 1e5 + 10;
int son[N][26], cnt[N], idx;
// 下标0代表根节点和空节点，cnt用于计数，idx代表结点的索引

void insert(string s) {
    int x = 0;
    for (auto c: s) {
        int y = c - 'a';
        if (!son[x][y]) son[x][y] = ++idx;// 没有该子结点就创建一个
        x = son[x][y]; // 走到该子节点
    }
    ++cnt[x];// 标记该子节点存在的单词个数
}

int query(string s) {
    int x = 0;
    for (auto c: s) {
        int y = c - 'a';
        if (!son[x][y]) return 0;// 没有该子结点就返回查询不到
        x = son[x][y];
    }
    return cnt[x];
}


signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int n;
    cin >> n;
    while (n--) {
        string op, s;
        cin >> op >> s;
        if (op == "I") insert(s);
        else cout << query(s) << endl;
    }


    return 0;
}

【模板】字典树

https://www.luogu.com.cn/problem/P8306

题目描述

给定 n n n 个模式串 s 1 , s 2 , … , s n s_1, s_2, \dots, s_n s1​,s2​,…,sn​ 和 q q q 次询问，每次询问给定一个文本串 t i t_i ti​，请回答 s 1 ∼ s n s_1 \sim s_n s1​∼sn​ 中有多少个字符串 s j s_j sj​ 满足 t i t_i ti​ 是 s j s_j sj​ 的前缀。

一个字符串 t t t 是 s s s 的前缀当且仅当从 s s s 的末尾删去若干个（可以为 0 个）连续的字符后与 t t t 相同。

输入的字符串大小敏感。例如，字符串 Fusu 和字符串 fusu 不同。

输入格式

本题单测试点内有多组测试数据。

输入的第一行是一个整数，表示数据组数 T T T。

对于每组数据，格式如下：
第一行是两个整数，分别表示模式串的个数 n n n 和询问的个数 q q q。
接下来 n n n 行，每行一个字符串，表示一个模式串。
接下来 q q q 行，每行一个字符串，表示一次询问。

输出格式

按照输入的顺序依次输出各测试数据的答案。
对于每次询问，输出一行一个整数表示答案。

样例 #1

样例输入 #1

3
3 3
fusufusu
fusu
anguei
fusu
anguei
kkksc
5 2
fusu
Fusu
AFakeFusu
afakefusu
fusuisnotfake
Fusu
fusu
1 1
998244353
9

样例输出 #1

2
1
0
1
2
1

提示

数据规模与约定

对于全部的测试点，保证 1 ≤ T , n , q ≤ 1 0 5 1 \leq T, n, q\leq 10^5 1≤T,n,q≤105，且输入字符串的总长度不超过 3 × 1 0 6 3 \times 10^6 3×106。输入的字符串只含大小写字母和数字，且不含空串。

说明

std 的 IO 使用的是关闭同步后的 cin/cout，本题不卡常。

思路

因为这里需要统计的是前缀，因此每走一个点，都需要将cnt数组加1

这里不仅有小写，还有大写和数字，可以把小写映射为0-26,大写映射为26-52,数字映射为36-62 ,都是左闭右开区间。

有多组测试数据，需要初始化son为0，idx为0，cnt为0

数据比较大，需要开cin和cout优化

Trie第一维开多大取决于字符串长度,与idx能增长到多少有关，尽可能开大一点5e6没问题，第二维取决于字符串里面字符的个数

代码

/**
 * https://www.luogu.com.cn/problem/P8306
 */
#include <bits/stdc++.h>

#define int long long
using namespace std;

//空间怎么看开多大？看数据范围 输入总字符串总长度不超过3e6
const int N = 3e6 + 10;
int son[N][65], cnt[N], idx;

int get(char c) {
    if (c >= 'a' && c <= 'z') return c - 'a';
    if (c >= 'A' && c <= 'Z') return c - 'A' + 26;
    if (c >= '0' && c <= '9') return c - '0' + 26 + 26;

}

void insert(string s) {
    int x = 0;
    for (char c: s) {
        int y = get(c);
        if (!son[x][y]) son[x][y] = ++idx;
        x = son[x][y];
        cnt[x]++;
    }
}

int query(string s) {
    int x = 0;
    for (auto c: s) {
        int y = get(c);
        if (!son[x][y]) return 0;
        x = son[x][y];
    }
    return cnt[x];
}


void solve() {
    int n, q;
    cin >> n >> q;
    string s;
    while (n--) { cin >> s, insert(s); }
    while (q--) { cin >> s, cout << query(s) << '\n'; }

    //清空字典树,不使用memset,使用for
    for (int i = 0; i <= idx; i++) {
        for (int j = 0; j < 63; j++) {
            son[i][j] = 0;
        }
    }
    for (int i = 0; i <= idx; i++) cnt[i] = 0;
    idx = 0;
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
    int t;
    cin >> t;
    while (t--) solve();
    return 0;
}

AcWing 143. 最大异或对

在给定的 N N N 个整数 A 1 ， A 2 … … A N A_1，A_2……A_N A1​，A2​……AN​ 中选出两个进行 x o r xor xor（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数 N N N。

第二行输入 N N N 个整数 A 1 A_1 A1​～ A N A_N AN​。

输出格式

输出一个整数表示答案。

数据范围

1 ≤ N ≤ 1 0 5 1 \le N \le 10^5 1≤N≤105,
0 ≤ A i < 2 31 0 \le A_i < 2^{31} 0≤Ai​<231

输入样例：

3
1 2 3

输出样例：

3

思路

先将所有数插入到01Trie树中，然后遍历一遍数组，去找可以使得和他异或起来最大的数，时间复杂度是 n l o g n nlogn nlogn的，因为树每层最多30个.

如何找异或起来最大：

比如当前节点为0，那就看!0的节点是否存在，如果存在，走过去一定是最优的，因为在这一位异或起来的结果就可以变成1了，否则只能往0走。

代码

/**
 * https://www.acwing.com/problem/content/145/
 */
#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 1e5 + 10;
int son[N * 32][2], idx;

void insert(int t) {
    int x = 0;
    for (int i = 30; i >= 0; i--) {
        int y = t >> i & 1;
        if (!son[x][y]) son[x][y] = ++idx;
        x = son[x][y];
    }
}

int query(int t) {
    int x = 0, res = 0;
    for (int i = 30; i >= 0; i--) {
        int y = t >> i & 1;
        if (son[x][!y]) {//另一个存在
            res = res * 2 + !y;
            x = son[x][!y];
        } else {
            res = res * 2 + y;
            x = son[x][y];
        }
    }
    return res;
}


signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i)cin >> a[i];
    for (int i = 0; i < n; ++i) insert(a[i]);
    int mx = 0;
    for (int i = 0; i < n; ++i) mx = max(mx, a[i] ^ query(a[i]));
    cout << mx << endl;


    return 0;
}

最长异或路径

题目描述

给定一棵 n n n 个点的带权树，结点下标从 1 1 1 开始到 n n n。寻找树中找两个结点，求最长的异或路径。

异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

输入格式

第一行一个整数 n n n，表示点数。

接下来 n − 1 n-1 n−1 行，给出 u , v , w u,v,w u,v,w ，分别表示树上的 u u u 点和 v v v 点有连边，边的权值是 w w w。

输出格式

一行，一个整数表示答案。

样例 #1

样例输入 #1

4
1 2 3
2 3 4
2 4 6

样例输出 #1

7

提示

最长异或序列是 1 , 2 , 3 1,2,3 1,2,3，答案是 7 = 3 ⊕ 4 7=3\oplus 4 7=3⊕4。

数据范围

1 ≤ n ≤ 100000 ; 0 < u , v ≤ n ; 0 ≤ w < 2 31 1\le n \le 100000;0 < u,v \le n;0 \le w < 2^{31} 1≤n≤100000;0<u,v≤n;0≤w<231。

思路

要求两个点之间的所有元素的异或值，设为 i , j i,j i,j两点， 可以变成 i i i到根节点异或 j j j到根节点的异或值。

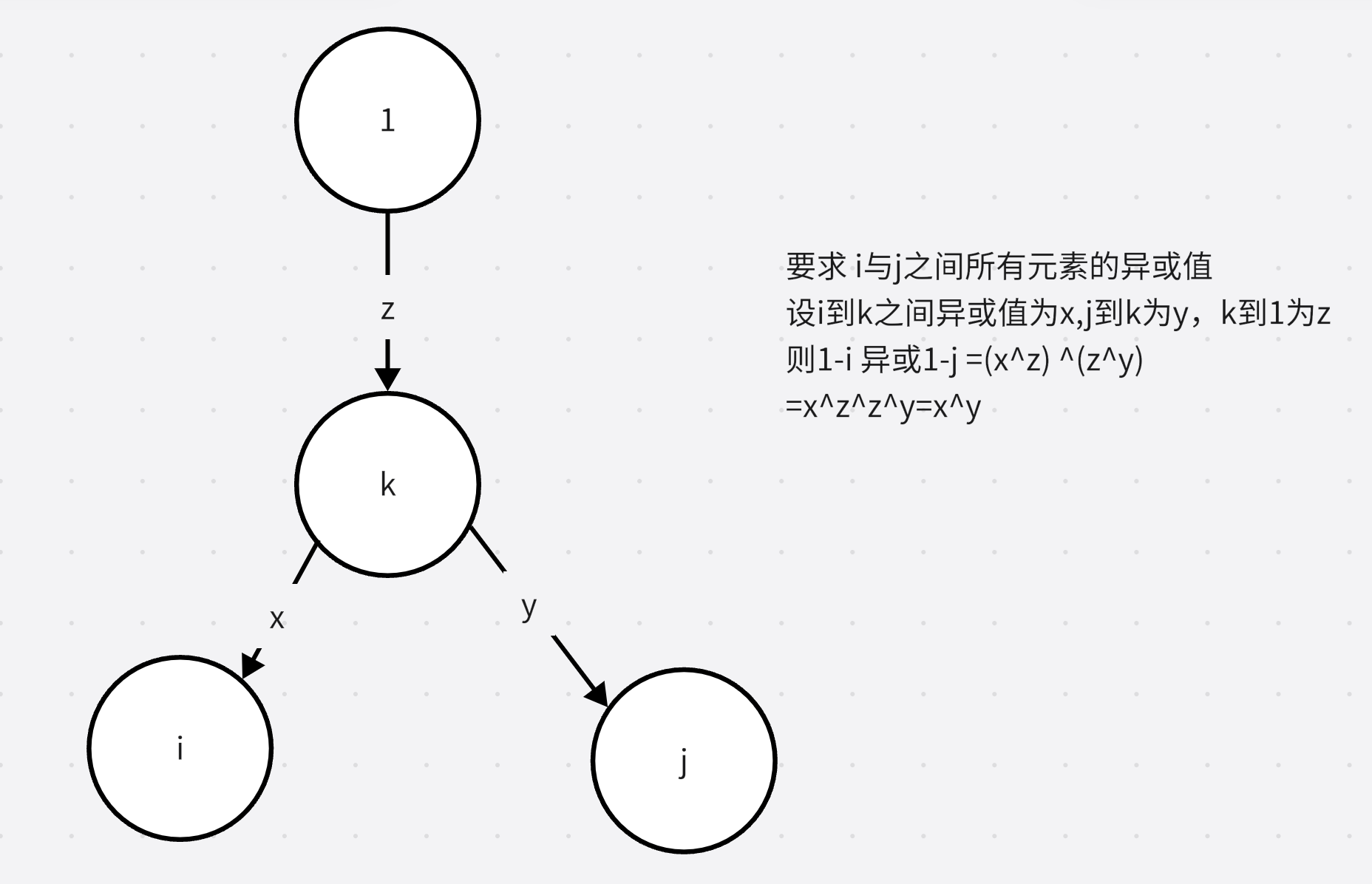
image-20230726161558142

因此我们可以去求每个点到根节点1的异或值，使用dfs即可，记录在sum中

然后遍历每个点，求当前点到根节点亦或值sum[i]可以异或得到的最大值。

之后就和上面一题一样了

代码

#include <bits/stdc++.h>

using namespace std;

typedef struct edge {
    int to, w;
} edge;

const int N = 1e5 + 10;
int son[N * 31][2], cnt[N], idx;
int sum[N];// 存到根节点到异或值
vector<edge> e[N];
int n;

void dfs(int x, int fa) {
    for (auto [y, w]: e[x]) {
        if (y == fa) continue;
        sum[y] = sum[x] ^ w;
        dfs(y, x);
    }
}

void insert(int t) {
    int x = 0;
    for (int i = 30; i >= 0; i--) {
        int y = t >> i & 1;
        if (!son[x][y]) son[x][y] = ++idx;
        x = son[x][y];
    }
}

int query(int t) {
    int x = 0, res = 0;
    for (int i = 30; i >= 0; i--) {
        int y = t >> i & 1;
        if (son[x][!y]) {
            res += 1 << i;
            x = son[x][!y];
        } else {
            x = son[x][y];
        }
    }
    return res;
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> n;
    for (int i = 1; i <= n - 1; i++) {
        int x, y, w;
        cin >> x >> y >> w;
        e[x].push_back({y, w});
        e[y].push_back({x, w});
    }
    dfs(1, 0);
    for (int i = 1; i <= n; i++) insert(sum[i]);
    int res = 0;
    for (int i = 1; i <= n; i++) res = max(res, query(sum[i]));
    cout << res << endl;

    return 0;
}

最小异或对

题目描述

https://ac.nowcoder.com/acm/contest/53485/F

给出一个多重集合(元素可以重复的集合),你需要提供以下操作:

  1. ADD x,向多重集合里添加一个元素x,多重集合内元素可以重复
  2. **DEL x,**从多重集合中删除一个元素x,保证要删除的元素一定存在,如果存在多个x则仅删除其中任意1个
  3. QUE,查询集合中的最小异或对的值,即找到集合中任何**两个元素(可以相等)**异或能得到的最小值,保证询问时集合包含的元素数量不少于2个

对于每个QUE操作,你需要输出查询的结果.

以上操作中涉及的操作数x均为非负整数.

1 < = n < = 2 ∗ 1 0 5 , 0 < = x < 2 30 1<=n<=2*10^5 ,0<=x<2^{30} 1<=n<=2∗105,0<=x<230

思路-01Trie

与最大异或对类似

思路-结论

最小异或对的结论：最小异或对一定为数组排序后相邻两个数的异或值

证明：

设 a < b < c a<b<c a<b<c,我们现在需要证明最小异或对只可能是ab或者bc

设c与a的第一个不同的位为第x位(从高向低看),则x位上面c一定为1，a一定为0 ,b可以为0或者1

a,b,c在x位置之前的数字都是相同的。

因此在x位上面，ac的这一位一定为1，ab和b^c一定会有一个异或起来在这一位为0，

因此a^c不可能是最小的，也就是一定是相邻两个数异或起来才是最小。

可以使用平衡树进行增删改查操作.

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

multiset<int> s, res;
int n, x;
string op;

void add() {
    auto it = s.lower_bound(x);
    if (it != s.end()) res.insert(x ^ *it);
    if (it != s.begin()) res.insert(x ^ *prev(it));
    if (it != s.end() && it != s.begin()) res.erase(res.lower_bound(*it ^ *prev(it)));
    s.insert(x);
}

void del() {
    s.erase(s.find(x));
    auto it = s.lower_bound(x);
    if (it != s.end()) res.erase(res.find(x ^ *it));
    if (it != s.begin()) res.erase(res.find(x ^ *prev(it)));
    if (it != s.end() && it != s.begin()) res.insert(*it ^ *prev(it));
}

int que() {
    return *res.begin();
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> n;
    while (n--) {
        cin >> op;
        if (op == "ADD") {
            cin >> x;
            add();
        } else if (op == "DEL") {
            cin >> x;
            del();
        } else cout << que() << endl;
    }

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/799987.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

欧姆龙 NJ SNMP 协议的使用，用于监控PLC的网络状态

欧姆龙 NJ SNMP 协议的使用，用于监控PLC的网络状态

NJ SNMP 协议的使用 实验时间&#xff1a;2023.07.25 实验器材&#xff1a;NJ501-1300 实验目的&#xff1a;NJ SNMP 协议的使用 1. SNMP 协议介绍 ​ SNMP&#xff08;Simple Network Management Protocol&#xff09;是一种简单网络管理协议。它属于 TCP/IP 五层协议中的…
阅读更多...
Cerbero Suite Advanced Crack

Cerbero Suite Advanced Crack

Cerbero Suite Advanced Crack 用于软件分类和文件分析的最先进的工具套件。分析多种文件格式&#xff0c;包括PE、Mach-O、ELF、Java、SWF、DEX、PDF、DOC、XLS、RTF、Zip等。 它提供自动分析、交互式分析、Carbon interactive Disassembler、字节码反汇编程序、带布局的十六进…
阅读更多...
一篇文章搞定《EventBus详解》

一篇文章搞定《EventBus详解》

一篇文章搞定《EventBus详解》 前言EventBus简述EventBus的使用EventBus源码解析初始化并构建实例EventBus.getDefault()EventBus.builder()EventBus初始化的重要成员 注册流程register方法SubscriberMethodFinder类findSubscriberMethods方法findUsingReflection方法&#xff…
阅读更多...
掌握Python的X篇_10+11_if分支语句、else语句、elif语句

掌握Python的X篇_10+11_if分支语句、else语句、elif语句

文章目录 1. if关键字及语法2. 语句块的概念3. else语句4. elif语句 1. if关键字及语法 基本语法如下&#xff1a; if 条件表达式:条件为True时&#xff0c;要执行的语句举例&#xff1a; number int(input("Input an number")) if number > 5 :print("这…
阅读更多...
【Spring框架】spring对象注入的三种方法

【Spring框架】spring对象注入的三种方法

目录 1.属性注入问题&#xff1a;同类型的Bean存储到容器多个&#xff0c;获取时报错的问题&#xff1b;1.将属性的名字和Bean的名字对应上。2.使用AutoWiredQualifier来筛选bean对象&#xff1b; 属性注入优缺点 2.Setter注入Setter注入优缺点 3.构造方法注入&#xff08;Spri…
阅读更多...
Node.js 安装与版本管理（nvm 的使用）

Node.js 安装与版本管理（nvm 的使用）

安装 Node.js Node.js 诞生于 2009 年 5 月&#xff0c;截至今天&#xff08;2022 年 3 月 26 号&#xff09;的最新版本为 16.14.2 LTS 和 17.8.0 Current&#xff0c;可以去官网下载合适的版本。 其中&#xff0c;LTS&#xff08;Long Term Support&#xff09; 是长期维护…
阅读更多...
MySQL基础扎实——主键与候选键

MySQL基础扎实——主键与候选键

词义解释 主键&#xff08;Primary Key&#xff09;和候选键&#xff08;Candidate Key&#xff09;是关系型数据库中的术语&#xff0c;用于标识和唯一确定表中的记录。它们之间有以下区别&#xff1a; 唯一性&#xff1a;主键是表中的唯一标识&#xff0c;每个表只能有一个主…
阅读更多...
环境保护数据传输系统监测环境指标

环境保护数据传输系统监测环境指标

嵌入式实时操作系统&#xff08;RTOS&#xff09;是一种专门设计用于嵌入式系统的操作系统。它具有实时性能和低延迟的特点&#xff0c;能够满足对时间响应性要求较高的应用。本文介绍了一种具备Modbus Slave和Modbus Master功能的嵌入式实时操作系统设备&#xff0c;以及其扩展…
阅读更多...
OpenGL Metal Shader 编程：ShaderToy 内置全局变量

OpenGL Metal Shader 编程：ShaderToy 内置全局变量

OpenGL & Metal Shader 编程&#xff1a;ShaderToy 内置全局变量 前面发了一些关于 Shader 编程的文章&#xff0c;有读者反馈太碎片化了&#xff0c;希望这里能整理出来一个系列&#xff0c;方便系统的学习一下 Shader 编程。 由于主流的 Shader 编程网站&#xff0c;如…
阅读更多...
Dart - 语法糖（持续更新）

Dart - 语法糖（持续更新）

文章目录 前言开发环境中间表示语法糖1. 操作符/运算符&#xff08;?./??/??/../?../.../...?&#xff09;2. 循环&#xff08;for-in&#xff09;3. 函数/方法&#xff08;>&#xff09;4. 关键字&#xff08;await for&#xff09; 最后 前言 通过将dill文件序列化…
阅读更多...
【时间序列预测 2023 ICLR】TimesNet

【时间序列预测 2023 ICLR】TimesNet

【时间序列预测 2023 ICLR】TimesNet 论文题目&#xff1a;TIMESNET: TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS 中文题目&#xff1a;TimesNet:用于一般时间序列分析的时态二维变异建模 论文链接&#xff1a;https://arxiv.org/abs/2210.02186 论文代…
阅读更多...
大专同事一个人7天完成CRM系统开发，怪不得月薪3w

大专同事一个人7天完成CRM系统开发，怪不得月薪3w

在当今的快节奏商业环境中&#xff0c;成功的关键是敏捷和高效。这使得开发自己的客户关系管理系统&#xff08;CRM&#xff09;成为许多企业的迫切需求。CRM有助于跟踪和优化销售线索&#xff0c;管理客户交互&#xff0c;并提高业务效率。但是&#xff0c;对于许多企业来说&a…
阅读更多...
大学毕业后，我就去当了2个月外卖骑手，哭了一整晚

大学毕业后，我就去当了2个月外卖骑手，哭了一整晚

先简单介绍一下自己&#xff0c;我来自长沙&#xff0c;大学学的的物流管理专业&#xff0c;现在就职于一家互联网公司&#xff0c;从事软件测试工作。 我来自长沙县的一个偏远农村&#xff0c;家里兄弟姐妹多&#xff0c;父母无力负担我的学费&#xff0c;很多时候学费都是靠姐…
阅读更多...
智慧工厂4G+蓝牙+UWB+RTK人员定位系统解决方案

智慧工厂4G+蓝牙+UWB+RTK人员定位系统解决方案

人员定位在智慧工厂的应用正逐渐受到重视&#xff0c;通过使用现代化的技术和智能终端设备&#xff0c;工厂管理者能够实时定位和跟踪员工的位置&#xff0c;方便进行人员调度管理和监督人员的工作情况&#xff1b;人员遇到紧急情况&#xff0c;可通过定位设备一键报警求救&…
阅读更多...
智慧消防：如何基于视频与智能分析技术搭建可视化风险预警平台？

智慧消防：如何基于视频与智能分析技术搭建可视化风险预警平台？

一、背景分析 消防安全是一个重要的话题&#xff0c;涉及到每个人的生活和安全。每年都会发生大量的火灾&#xff0c;给人们带来极大的危害&#xff0c;摧毁了大量的财产&#xff0c;甚至造成了可怕的人员伤亡。而消防安全监督管理部门人员有限&#xff0c;消防安全监管缺乏有…
阅读更多...
2.2 模型与材质基础

2.2 模型与材质基础

一、渲染管线与模型基础 1. 渲染管线 可编程阶段&#xff08;蓝色区域&#xff09;&#xff1a; 1顶点着色器 2几何着色器 3片元着色器 2. 模型的实现原理 UV&#xff1a;在建模软件中&#xff0c;进行UV展开&#xff0c;UV会放在一个横向为U纵向为V&#xff0c;范围&#xff0…
阅读更多...
TEE GP(Global Platform)功能认证实验室

TEE GP(Global Platform)功能认证实验室

TEE之GP(Global Platform)认证汇总 GP认证实验室主要面向功能认证、SE安全认证、TEE安全认证&#xff0c;对于TEE来说&#xff0c;则分为TEE功能认证和TEE安全认证。本文对功能认证相关实验室机构进行总结和介绍。 一、国内3家 二、国外3家 参考&#xff1a; GlobalPlatform …
阅读更多...
回归预测 | MATLAB实现POA-CNN-BiLSTM鹈鹕算法优化卷积双向长短期记忆神经网络多输入单输出回归预测

回归预测 | MATLAB实现POA-CNN-BiLSTM鹈鹕算法优化卷积双向长短期记忆神经网络多输入单输出回归预测

回归预测 | MATLAB实现POA-CNN-BiLSTM鹈鹕算法优化卷积双向长短期记忆神经网络多输入单输出回归预测 目录 回归预测 | MATLAB实现POA-CNN-BiLSTM鹈鹕算法优化卷积双向长短期记忆神经网络多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 MATLA…
阅读更多...
安全杂记 - js中的this关键字

安全杂记 - js中的this关键字

javascript里什么是this this是js中的一个关键字&#xff0c;它是函数在运行时生成的一个内部对象&#xff0c;是属性和方法。 this就是属性或方法“当前”所在的对象&#xff0c;也就是调用函数的那个对象 this的使用场合 1.函数调用 <script>var a100;function test…
阅读更多...
jenkins部署vue项目

jenkins部署vue项目

文章目录 1 先安装node.js上传到linux并解压 jenkins 创建任务执行脚本 build Stepsvue jenkins shell 脚本 (jenkins-web.sh)启动 如何在linux上安装jenkins可以看上一篇 linux安装jenkins(详细步骤) 1 先安装node.js 建议最好跟你本地安装版本一致,减少没有必要的麻烦:node.…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023