目录标题
- NO1:数组中重复的数字(简单)
- 题目详细&做题链接
- 解法一:辅助数组
- 解法二:排序
- 解法三:交换数据
- 解法四:二分查找
- NO2:二维数组的查找(中等)
- 题目详细&做题链接
- 解法一:暴力查找
- 解法二:从右向左查找
- 解法三:从左向右查找
- NO3:替换空格
- 题目详细&做题链接
- 解法一:辅助容器
- 解法二:移动数据
NO1:数组中重复的数字(简单)
题目详细&做题链接

做题链接->点击此处尝试做题
解法一:辅助数组
这里是找到出现重复的数字,所以我们有个很直白的思路就是创建一个辅助容器来帮助我们计数,根据题目的阐述我们可以把数据的情况分为三种:1.数据没有出现 2.数据出现了一次 3.数据重复出现了多次,所以我们可以创建一个vector容器且元素的类型为bool,初始化容器的时候将容器的大小开辟为参数vector相同的大小并且每个元素都初始化为false,比如说下面的代码:
int findRepeatNumber(vector<int>& nums) {
size_t _size=nums.size();
vector<bool> flag(_size,false);
}
因为题目告诉我们数组nums的内部数据范围是0~n-1,所以我们就可以采用直接映射的方式来修改flag数组里面的内容,比如说nums数组中出现了1,那么我们就去修改flag数组中下标为1的数据,如果下标为1的数据之前为false的话就将其修改为true,如果之前为true的话就直接返回1来结束该函数表示我们已经找到了重复数据1,那么这里的代码就如下:
int findRepeatNumber(vector<int>& nums) {
size_t _size=nums.size();
vector<bool> flag(_size,false);
for(int i=0;i<_size;i++)
{
if(flag[nums[i]]==true)
{
return nums[i];
}
flag[nums[i]]=true;
}
return -1;//返回-1表示当前数组没有出现重复数据。
}
测试的结果如下:

解法一的时间复杂度为O(N),空间复杂度为O(N)
解法二:排序
解法一的思路是创建一个辅助数组来帮助我们计数从而找到重复的数据,那么题目要是添加限制规定空间复杂度必须得为O(1),那解法一的思路就不适用了对吧!所以解法二的思路就是先对nums数组进行排序,当数组内部的数据有序之后重复数据所在的位置就会挨在一起,那么我们就可以创建两个变量一起来记录数组中相邻位置的元素,然后循环遍历整个数组并修改两个变量的值,一旦遍历的过程两个变量的值相等就表明当前的变量所记录的元素为重复元素,那么这里的代码就如下:
int findRepeatNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int cur = 0;
int next = 0;
for (size_t i = 1; i < nums.size(); i++)
{
cur = nums[i - 1];
next = nums[i];
if (cur == next)
{
return cur;
}
}
return -1;
}
代码的测试结果如下:

解法二的时间复杂度为O(N),空间复杂度为O(1)
解法三:交换数据
数据范围为0~N-1而数组的大小为N,所以当数组内部没有重复数据时,数组中的每个数据都应该有下标与之对应,所以解法三的思路就是通过不停的交换元素找到下标与之对应的元素,找到了我们就继续对下一个位置进行查找,元素的交换过程如下:

首先检查下标为0的元素2,2不等于0所以要对该元素进行交换,那么这里存在一个问题它要跟哪个元素进行交换呢?答案是跟它值所对应下标的元素进行交换,值为2不等于它的下标0,所以要跟下标为2的元素进行交换,这样2就来到了它应该所在的位置,交换之后的图片就变成了下面这样:

交换完之后下标为0的元素为刚好为0所以0位置的元素就确定,所以我们对下个位置的元素进行交换,也就是对下标为1的元素进行交换,而1下标对应的元素刚好为1不需要交换,所以接着跳转到下标2,同样的道理下标为2的元素也确定了不需要交换,所以我们跳转到了下标3,这时下标3的元素为1不等于3,所以我们要对该数据进行交换,交换的对象为下标为1的元素,可是下标为1的元素也是1那么这时我们就找到重复的元素,也就是说交换元素时发现交换的元素和当前元素相等,就表明我们找到了重复元素,那么实现代码的第一步就是创建一个for循环,表示对数据每个下标的元素都要进行交换,找到其对应的元素:
int findRepeatNumber(vector<int>& nums) {
for(size_t i=0;i<nums.size();i++)
{
while(nums[i]!=i)
{
}
}
}
因为一个位置的元素可能需要交换很多次才能找到相匹配的,所以在for循环的内部还得创建一个while循环,循环结束的条件就是元素的值和下标的值相等,在while循环里面就是将当前位置的值与该值对应位置的元素进行交换,那么这里的代码就如下:
int findRepeatNumber(vector<int>& nums) {
for(size_t i=0;i<nums.size();i++)
{
while(nums[i]!=i)
{
swap(nums[i],nums[nums[i]]);
}
}
}
但是交换的过程中可能会出现两个位置的值相等也就是出现数据重复的情况,那么这时我们就应该使用return来结束函数,所以这里还得添加一个if语句用来做出判断,那么完整的代码就如下:
int findRepeatNumber(vector<int>& nums) {
for(size_t i=0;i<nums.size();i++)
{
while(nums[i]!=i)
{
if(nums[i]==nums[nums[i]])
//出现相等表明重复这个时候直接返回
{
return nums[i];
}
swap(nums[i],nums[nums[i]]);
}
}
return -1;
}
测试的结果如下:

这种解法的时间复杂度为O(N),空间复杂度为O(1).
解法四:二分查找
如果题目添加要求说当前题目不能对原数组进行修改并且空间复杂度还得是o(1)的话,那我们该如何来进行解答呢?那么这里我们就可以尝试使用二分查找来进行解答,数据的范围是0~n-1那么我们首先就可以判断0~(n-1)/2的数据个数是否是正常的,如果没有重复这个范围里面的数据个数是sum,然后我们就可以统计这个数组里面该范围的数据个数,如果统计出来的数据个数大于sum的话就说明这个范围里面一定存在重复的数据,那么我们就可以缩小一半的范围然后继续判断,如果统计出来的数据个数等于或者小于sum的话就说明重复的数据出现在另外一半,然后我们就可以更改范围然后继续统计,将上面的思路转换成为代码就变成下面这样:
//这个函数用于计算范围内数据出现的个数
int countnum(int left,int right,vector<int>& nums)
{
int total=0;
for(auto ch:nums)
{
if(ch>=left&&ch<=right)
{
total++;
}
}
return total;
}
int findRepeatNumber(vector<int>& nums) {
int end=nums.size()-1;
int start=0;
while(start<end)
{
int mid=start+(end-start)/2;
int count=countnum(start,mid,nums);
if(count>(mid-start+1))
{
end=mid;
}
else
{
start=mid+1;
//这里的+1很重要,不然会出现死循环
}
}
return start;
}
将代码运行一下可以看到这里报错了:
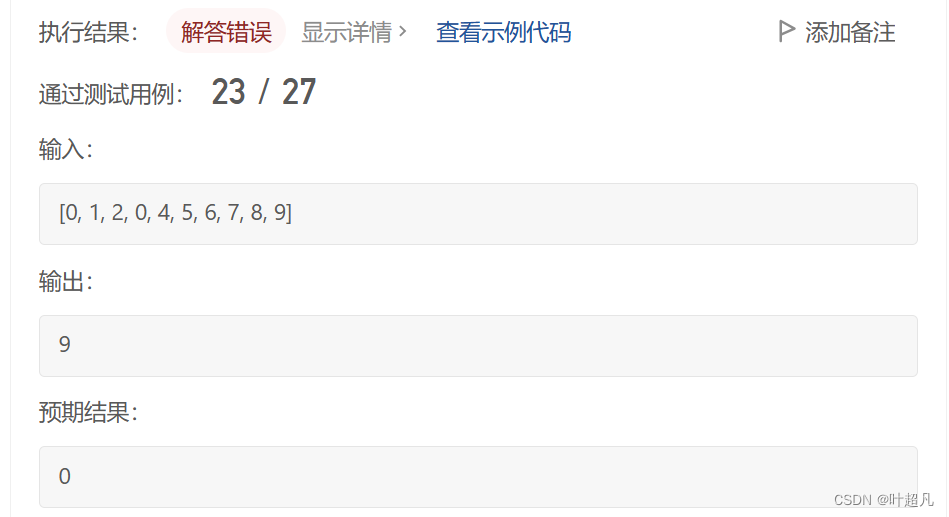
可以看到这里通过了一大半的测试用例,那这里为什么出错了呢?原因是二分查找存在问题,如果我们统计的数据过多,那么一定能够说明当前范围存在重叠的数据,如果等于了能够说明重叠的数据在另外一半吗?好像不能对吧,我们看上面的例子start等于0mid算出来等于4,在统计数据的时候我们发现0~4之间的数据个数也刚好是5,但是0~4之间存在重叠的数据,当我重叠了一个数据但是这个范围里面的数据又刚好有一个没有出现的话,那这个时候我们就不能判断重叠数据出现的方向是在左边还是右边了,所以我们可以再添加一个判断的分支,当出现相等的时候我们就可以使用两个for循环嵌套检查一下,如果出现了就直接返回,如果没有出现就说明重叠的数据在另外一段,那么修改之后的代码就如下:
int countnum(int left,int right,vector<int>& nums)
{
int total=0;
for(auto ch:nums)
{
if(ch>=left&&ch<=right)
{
total++;
}
}
return total;
}
int findRepeatNumber(vector<int>& nums) {
int end=nums.size()-1;
int start=0;
while(start<end)
{
int mid=start+(end-start)/2;
int count=countnum(start,mid,nums);
if(count>(mid-start+1))
{
end=mid;
}
else if(count==(mid-start+1))
{
for(int i=start;i<=end;i++)
{
if(countnum(i,i,nums)>1)
{
return i;
}
}
//走到这里就说明没有重叠
start=mid+1;
}
else
{
start=mid+1;
}
}
return start;
}
运行一下之前没有通过的测试用例可以看到测试通过了:
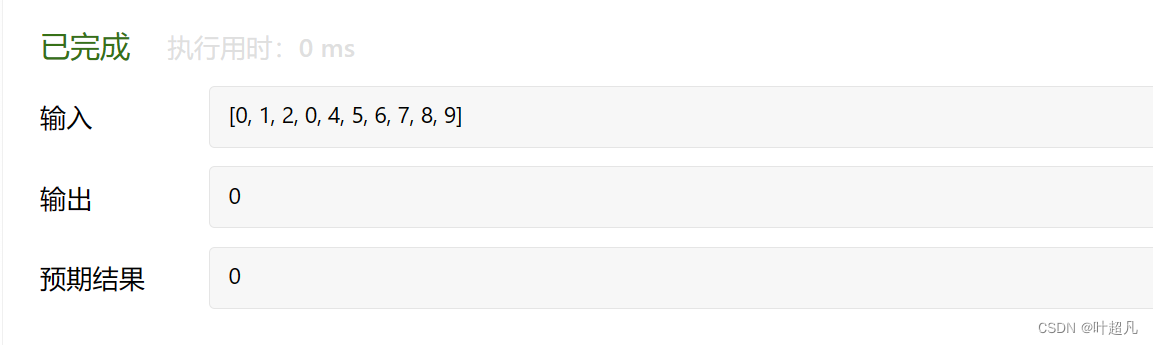
但是这么做的时间成本太高了,导致面对特别多数据的时候容易超出时间限制,所以对于这种题还是不太适合二分查找这种方法:

那么这就是本题的全部解析。
NO2:二维数组的查找(中等)
题目详细&做题链接

做题链接->点击此处尝试做题
解法一:暴力查找
题目要求我们从一个数组里面查找一个整数,那么我们有一个非常直接的思路就是遍历整个二维数组一个元素一个元素的进行查找,那么这里我们可以使用嵌套的for循环来完成二维数组的遍历,那么这里的代码就如下:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target)
{
int row=matrix.size();//行
if(row==0)
{
return false;
}
int col=matrix[0].size();//列
for(int i=0;i<row;i++)
{
for(int j=0;j<col;j++)
{
if(matrix[i][j]==target)
{
return true;
}
}
}
//遍历到这里说明当前没有找到相等的数据直接返回false表示不存在
return false;
}
这里大家要注意一点;参数传递过来的数组可能一个元素都没有,所以在创建完变量row之后我们得使用if语句判断一下,如果这个数组连一行数据都没有的话我们就直接return来结束该函数,不然后面创建变量col时就会报错,那么代码的测试运行的结果如下:
 可以看到暴力查找的方法是可以通过的,这种方法的时间复杂度是o(N),空间复杂度为o(1)。
可以看到暴力查找的方法是可以通过的,这种方法的时间复杂度是o(N),空间复杂度为o(1)。
解法二:从右向左查找
使用暴力查找的方式来解决这道题很明显就没有利用好题目给我们的信息,我们再来仔细地观察一下题目给的图片:

它说每一行数据都从左往右是非递减的顺序来进行排列,每一列数据从上到下是非递减的顺序来进行排序,比如说下面的图片:

数据15位于第0行的第4列,那么如果一个数据比15还要大的话那么它肯定也比15所在行左边的数据都大,比如说查找数据16,16比15大所以16也会比15所在行的左边所有数据都要大,那么我们在查找的时候就不用比较这些数据了直接跳过,此时图片就变成了下面这样:

红色背景的图片就表示当前的数据已经被排除了不需要进行比较,蓝色背景的数据就表明当前要比较的数据,那么这时我们就要拿16和19进行比较,19比16大而且19下面的数据都比19大,所以19和19下面的数据都不是我们要找的数据可以直接跳过,要比较的数据也就来到19的左边,那么这时图片就变成了下面这样:

同样的道理16比12大所以12和12左边的数据都可以直接跳过,我们要比较的数据就来到了12的下方,那么这时的图片就变成了下面这样:
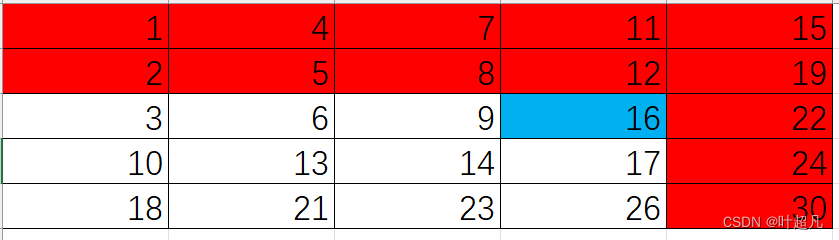
这时来到的数据刚好等于16所以我们就可以直接返回,这种方法进行比较的时候每次比较就可以过滤掉一行或者一列的数据比方法一要高效很多,那么这里就是抓住题目给出的规律来进行做题,好接下来我们就来看看上面的思路如何来进行实现,首先记录一下行和列的值并且判断一下当前数组中是否存在数据,判断完之后就讲行的值初始化为0,那么这里的代码如下:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int row=matrix.size();//行
if(row==0)
{
return false;
}
row=0;//因为从右上角进行比较所以这里将row赋值为0
int col=matrix[0].size();//列
}
然后我们就可以创建一个while循环进行查找,在循环里面如果发现当前位置的数据与查找的数据相等的话就直接返回true,如果当前位置的数据大于要查找的数据的话就对col的值进行减一,如果当前位置的数据小于要查找的数据的话就对row的值进行加一,那么这里的代码就如下:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int row=matrix.size();//行
if(row==0)
{
return false;
}
row=0;//因为从右上角进行比较所以这里将row赋值为0
int col=matrix[0].size()-1;//列
while()
{
if(matrix[row][col]==target)
{
return true;
}
else if(matrix[row][col]<target)
{
++row;
}
else
{
--col;
}
}
}
循环的内容写完了我们就来看看循环结束的条件,如果一个数据在数组里面不存在的话,那么我们查找的过程中会不断的对行进行加加或者对列进行减减如果一直循环下去肯定会超出范围,那么当行的值大于数组的行时或者当列的值小于0时我们就可以结束循环返回false表示数据不存在,那么完整的代码就如下:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int row=matrix.size();//行
if(row==0)
{
return false;
}
row=0;//因为从右上角进行比较所以这里将row赋值为0
int col=matrix[0].size()-1;//列
while(col>=0&&row<matrix.size())
{
if(matrix[row][col]==target)
{
return true;
}
else if(matrix[row][col]<target)
{
++row;
}
else
{
--col;
}
}
return false;
}
代码的测试结果如下:
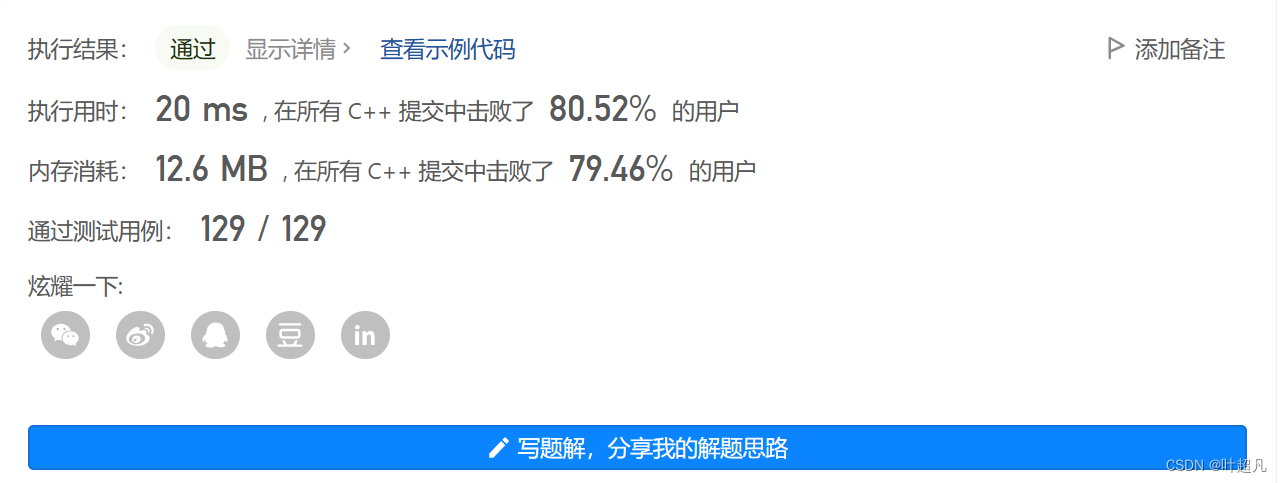
解法三:从左向右查找
既然可以从数组的右上角开始查找,那么同样的道理我们还可以从数组的左下角开始查找,那么这里的规律就变成如果查找的数据较大的话就将查找的范围往右边移动,如果查找的数据较小的话我们就向上进行移动,那么这里我们就对row和col的值进行以下改变,将col初始化为0,row初始化为数组的最下段,然后改变以下while循环结束条件和内部的循环内容就可以了,那么这里的代码如下:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
if(matrix.size()==0)
{
return false;
}
int col=0;//列
int row=matrix.size()-1;//行
while(row>=0&&col<matrix[0].size())
{
if(matrix[row][col]==target)
{
return true;
}
else if(matrix[row][col]<target)
{
++col;
}
else
{
--row;
}
}
return false;
}
代码的运行结果如下:

可以看到这种思路也是可行的,那么这就是本题的讲解。
NO3:替换空格
题目详细&做题链接

做题链接->点击此处尝试做题
解法一:辅助容器
题目的要求事将string对象里面的每个空格都替换成为%20,那么这里我们就可以再创建一个string类型的对象,然后遍历原来的容器,如果当前的数据不是空格的话我们就当前的数据插入到容器的尾部里面,如果当前的元素是空格的话我们就将字符串%20插入到容器的尾部,循环结束就将创建的对象进行返回即可,那么这里的代码就如下:
string replaceSpace(string s) {
string s1;
for(auto ch:s)
{
if(ch==' ')
{
s1+="%20";
}
else
{
s1+=ch;
}
}
return s1;
}
测试的结果如下:

这种方法的时间复杂度是o(N)空间复杂度也是o(N)。
解法二:移动数据
解法一是通过创建辅助容器来进行解决,那如果题目要求本题的空间复杂度必须得为o(1)的话我们就只能在容器里面进行操作,首先通过一个循环找到容器里面空格的数目,然后通过resize函数对容器的长度进行伸长使其增加空格数量的两倍,那么这里的代码如下:
string replaceSpace(string s) {
size_t nums=0;
int begin=s.size()-1;
for(auto ch: s)
{
if(ch==' ')
{
nums++;
}
}
s.resize(s.size()+nums*2);
}
创建一个变量end记录当前容器尾部的位置,然后我们再创建一个for循环遍从数据的尾部开始遍历整个数组,如果begin位置没有出现空格就将bgin位置的值赋值到end位置上去,如果出现空格了就将end位置和前两个位置赋值为%20,每次赋值都对begin和end的值进行减减,如果begin的值小于0了就说明赋值结束直接将s进行返回即可,那么这里的代码如下:
string replaceSpace(string s) {
size_t nums=0;
int begin=s.size()-1;
for(auto ch: s)
{
if(ch==' ')
{
nums++;
}
}
s.resize(s.size()+nums*2);
int end=s.size()-1;
for(;begin>=0;begin--)
{
if(s[begin]==' ')
{
s[end--]='0';
s[end--]='2';
s[end--]='%';
}
else
{
s[end--]=s[begin];
}
}
return s;
}
代码的测试的结果如下:

那么这种方法的时间复杂度为o(N),空间复杂度为o(1),那么到这里本篇文章就结束了谢谢大家阅读。