目录
- 第三章 栈和队列
- 3.1栈(stack)
- 3.1.1栈的基本概念
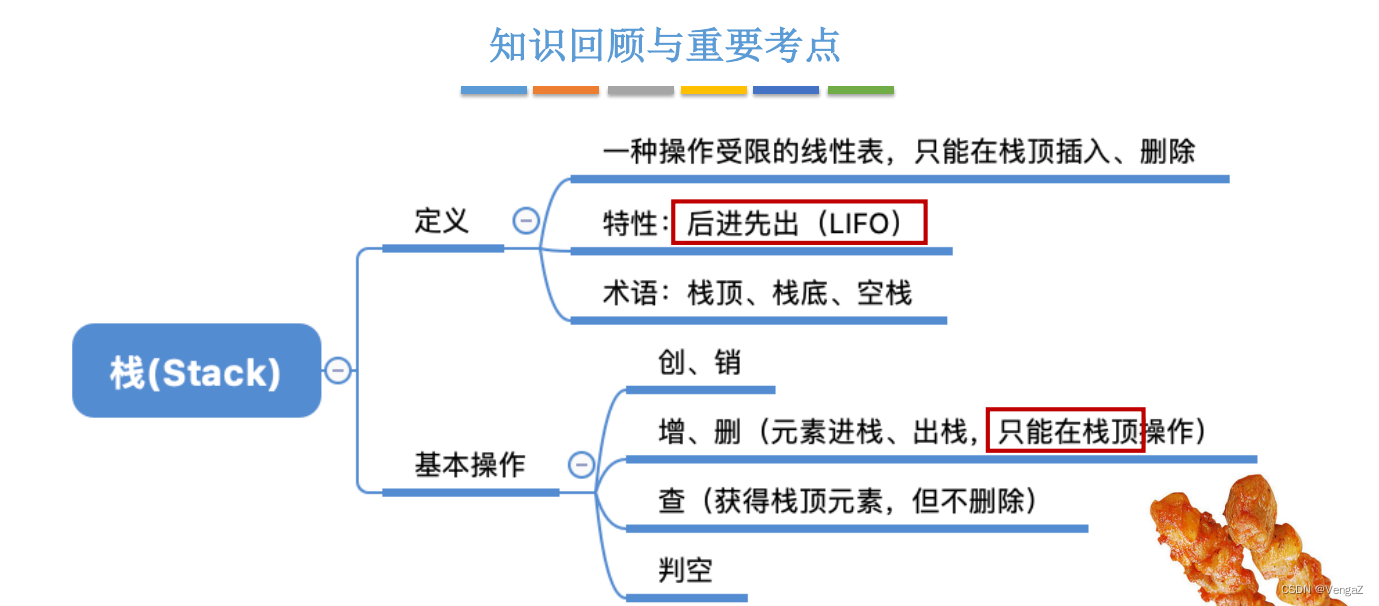
- 栈的基本概念知识回顾
- 3.1.2 栈的顺序存储
- 上溢与下溢
- 栈的顺序存储知识回顾
- 3.1.3栈的链式存储
- 链栈的基本操作
第三章 栈和队列
3.1栈(stack)
3.1.1栈的基本概念
- 栈的定义
- 栈是特殊的线性表:只允许在一端进行插入或删除操作, 其逻辑结构与普通线性表相同;
- 栈顶(Top):允许进行插入和删除的一端 (最上面的为栈顶元素);
- 栈底(Bottom):固定的,不允许进行插入和删除的一端 (最下面的为栈底元素);
- 空栈:不含任何元素的空表;
特点:LIFO 后进先出(后进栈的元素先出栈)可以实现特定的逻辑;
栈的增删改查操做的存取数据的时间复杂度均为O(1)
缺点:栈的大小不可变,解决方法——共享栈;
栈的数学性质: 卡特兰数
n个不同元素进栈,有
1
n
+
1
C
2
n
n
\frac{1}{n+1}C^{n}_{2n}
n+11C2nn种不同的出栈书顺序
- 栈的基本操作
“创建&销毁”
- InitStack(&S) 初始化栈:构造一个空栈S,分配内存空间;
- DestroyStack(&S) 销毁栈:销毁并释放栈S所占用的内存空间;
“增&删”
- Push(&S, x) 进栈:若栈S未满,则将x加入使其成为新栈顶;
- Pop(&S, &x) 出栈:若栈S非空,则弹出(删除)栈顶元素,并用x返回;
“查顶&判空”
- GetTop(S, &x) 读取栈顶元素:若栈S非空,则用x-返回栈顶元素;(栈的使用场景大多只访问栈顶元素);
- StackEmpty(S) 判空: 断一个栈S是否为空,若S为空,则返回true,否则返回false;
栈的基本概念知识回顾
3.1.2 栈的顺序存储
- 顺序栈的定义
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top; //栈顶元素
}SqStack;
void testStack(){
SqStack S; //声明一个顺序栈(分配空间)
//连续的存储空间大小为 MaxSize*sizeof(ElemType)
}
注意此处的 int top; //栈顶元素表示存储的是数组下标
其实用int * top用一个指针来实现逻辑也行
- 顺序栈的基本操作
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top; //栈顶元素
}SqStack;
分配的空间为 Maxsize*sizeof(ElemType),
但是是程序运行时系统分配的不是自己主动malloc的
所以不需要在最后free,所以只需要逻辑上回收将指针移动就行
//初始化栈
void InitStack(SqStack &S){
S.top = -1; //初始化栈顶指针
}
//判栈空
bool StackEmpty(SqStack S){
if(S.top == -1) //栈空
return true;
else //栈不空
return false;
}
//新元素进栈
bool Push(SqStack &S, ElemType x){
if(S.top == MaxSize - 1) //栈满
return false;
S.top = S.top + 1; //指针先加1
S.data[S.top] = x; //新元素入栈
/*
S.data[++S.top] = x;
*/
return true;
}
//出栈
bool Pop(SqStack &x, ElemType &x){
if(S.top == -1) //栈空
return false;
x = S.data[S.top]; //先出栈
S.top = S.top - 1; //栈顶指针减1
return true;
/*
x = S.data[S.top--];
*/
只是逻辑上的删除,数据依然残留在内存里
但是这个程序执行结束,对应的内存系统会自行回收
}
//读栈顶元素
bool GetTop(SqStack S, ElemType &x){
if(S.top == -1)
return false;
x = S.data[S.top]; //x记录栈顶元素
return true;
}
void testStack(){
SqStack S; //声明一个顺序栈(分配空间)
InitStack(S);
//...
}
另一种设置栈顶指针位置的方法:初始化时定义 S.top = 0 ;top指针指向下一个可以插入元素的位置,也就是栈顶元素的后一个位置。
(总的来说,之前那种方法是top指针指向已经有元素的位置并且top == -1为判空条件,这种方法是指向没有元素的位置并且top == 0为判空条件)
初始化时定义 S.top = 0:
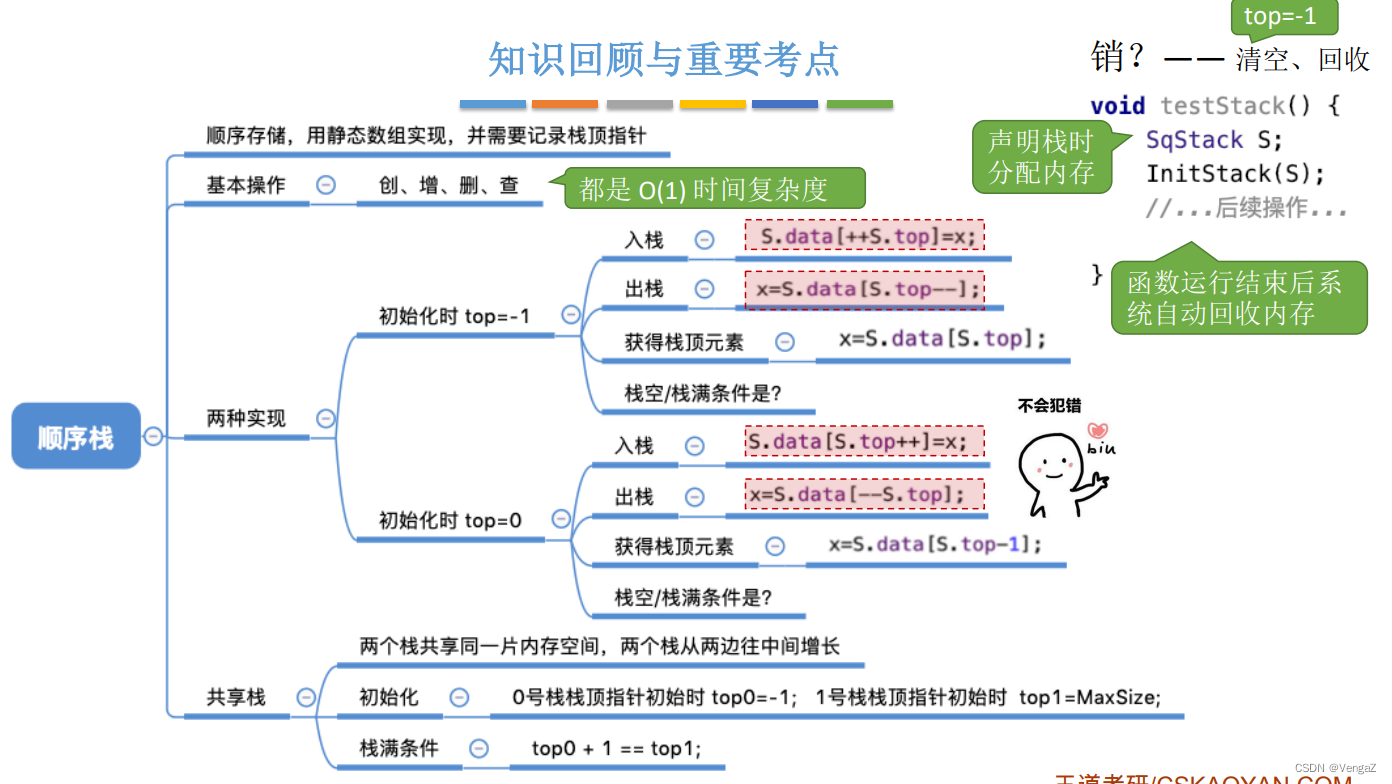
- 进栈操作 :栈不满时,栈顶指针先加1,再送值到栈顶元素。S.data[S.top++] = x;
- 出栈操作:栈非空时,先取栈顶元素值,再将栈顶指针减1。`x = S.data[–S.top];
- 栈空条件:S.top==-1
- 栈满条件:S.top==MaxSize-1
- 栈长:S.top+1
3.共享栈
定义:利用栈底位置相对不变的特性,可以让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸。

#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top0; //0号栈栈顶指针
int top1; //1号栈栈顶指针
}ShStack;
//初始化栈
void InitSqStack(ShStack &S){
S.top0 = -1; //初始化栈顶指针
S.top1 = MaxSize;
}
共享栈 栈满条件:S.top0 + 1 = S.top
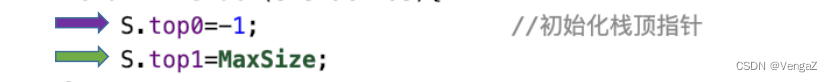
上溢与下溢
参考博客: 上溢与下溢
上溢与下溢分为堆栈的上溢与下溢和缓冲区的上溢和下溢
- 堆栈的上溢与下溢
堆栈区域是在堆栈定义时就确定了的,因而堆栈工作过程中有可能产生溢出。堆栈溢出有两种情况可能发生:如堆栈已满,但还想再存入信息,这种情况称为堆栈上溢;另一种情况是,如堆栈已空,但还想再取出信息,这种情况称为堆栈下溢。
采取保护措施:这可以通过给SP规定上、下限,在进栈或出栈操作前先做SP和边界值的比较,如溢出则作溢出处理,以避免破坏其他存储区或使程序出错的情况发生。
共享栈只有在整个对堆栈空间被占满才发生上溢,因为栈是只在头部进行操作的一种抽象数据结构,所以只可能发生上溢
- 缓冲区的上溢和下溢
上溢就是缓冲器满,还往里写;下溢就是缓冲器空,还往外读.
软件对硬件处理的不合理,速度的不一导致的上溢与下溢
如果指数据发送太快,硬件处理不过来,缓存已经装不下那么多数据,开始丢弃这些数据,放弃处理.这就是指上溢.
如果数据发送太慢,缓冲区的数据都处理空了,输入数据还没过来,硬件还在等待缓冲区有足够数据可以处理,输出接口就在要求发送处理好的数据出去,就是指下溢.
栈的顺序存储知识回顾
3.1.3栈的链式存储
- 定义:采用链式存储的栈称为链栈,且多采用单链表来实现。
- 优点:链栈的优点是便于多个栈共享存储空间和提高其效率,且不存在栈满上溢的情况。
- 特点:
进栈和出栈都只能在栈顶一端进行(链头作为栈顶)
链表的头部作为栈顶,意味着:(都是对链表的头进行操作)
- 在实现数据"入栈"操作时,需要将数据从链表的头部插入;
- 在实现数据"出栈"操作时,需要删除链表头部的首元节点;
因此,链栈实际上就是一个只能采用头插法插入或删除数据的链表;
栈的链式存储结构可描述为:
typedef struct Linknode{
ElemType data; //数据域
struct Linknode *next; //指针域
}*LiStack; //栈类型的定义
链栈的基本操作
- 初始化
- 进栈
- 出栈
- 获取栈顶元素
- 判空、判满
- 带头结点的链栈基本操作:
#include<stdio.h>
struct Linknode{
int data; //数据域
Linknode *next; //指针域
}Linknode,*LiStack;
typedef Linknode *Node; //结点结构体指针变量
typedef Node List; //结点结构体头指针变量
//1. 初始化
void InitStack(LiStack &L){ //L为头指针
L = new Linknode;
L->next = NULL;
}
//2.判栈空
bool isEmpty(LiStack &L){
if(L->next == NULL){
return true;
}
else
return false;
}
//3. 进栈(:链栈基本上不会出现栈满的情况)
void pushStack(LiStack &L, int x){
Linknode s; //创建存储新元素的结点
s = new Linknode;
s->data = x;
//头插法
s->next = L->next;
L->next = s;
}
//4.出栈
bool popStack(LiStack &L, int &x){
Linknode s;
if(L->next == NULL) //栈空不能出栈
return false;
s = L->next;
x = s->data;
L->next = L->next->next;
delete(s);
return true;
}
- 不带头结点的链栈基本操作:
#include<stdio.h>
struct Linknode{
int data; //数据域
Linknode *next; //指针域
}Linknode,*LiStack;
typedef Linknode *Node; //结点结构体指针变量
typedef Node List; //结点结构体头指针变量
//1.初始化
void initStack(LiStack &L){
L=NULL;
}
//2.判栈空
bool isEmpty(LiStack &L){
if(L == NULL)
return true;
else
teturn false;
}
//3.进栈
void pushStack(LiStack &L, int x){
Linknode s; //创建存储新元素的结点
s = new Linknode;
s->next = L;
L = s;
}
//4.出栈
bool popStack(LiStack &L, int &x){
Linknode s;
if(L = NULL) //栈空不出栈
return false;
s = L;
x = s->data;
L = L->next;
delete(s);
return true;
}








![[计算机入门] 操作项目](https://img-blog.csdnimg.cn/fe1d8684c7434e048e481aad5536be59.png)
![[OnWork.Tools]系列 02-安装](https://img-blog.csdnimg.cn/img_convert/5336a44e1bcedf8629368dc95cbe78ff.png)
