【强化学习】Q-learning训练AI走迷宫

news2024/11/18 21:28:29

0. 简单总结

Q-learning？

  • 最简单的强化学习算法！
  • 不需要深度学习网络的算法！
  • 带有概率性的穷举特性！（甚至还有一点点动态规划的感觉）

1. Q-learning介绍

Q-learning是一种基于强化学习的算法，用于解决Markov决策过程（MDP）中的问题。

这类问题我们理解为一种可以用有限状态机表示的问题。它具有一些离散的状态state、每一个state可以通过动作action转移到另外一个state。每次采取action，这个action都会带有一些奖励reward（也可以是负数，这样就表示惩罚了）。

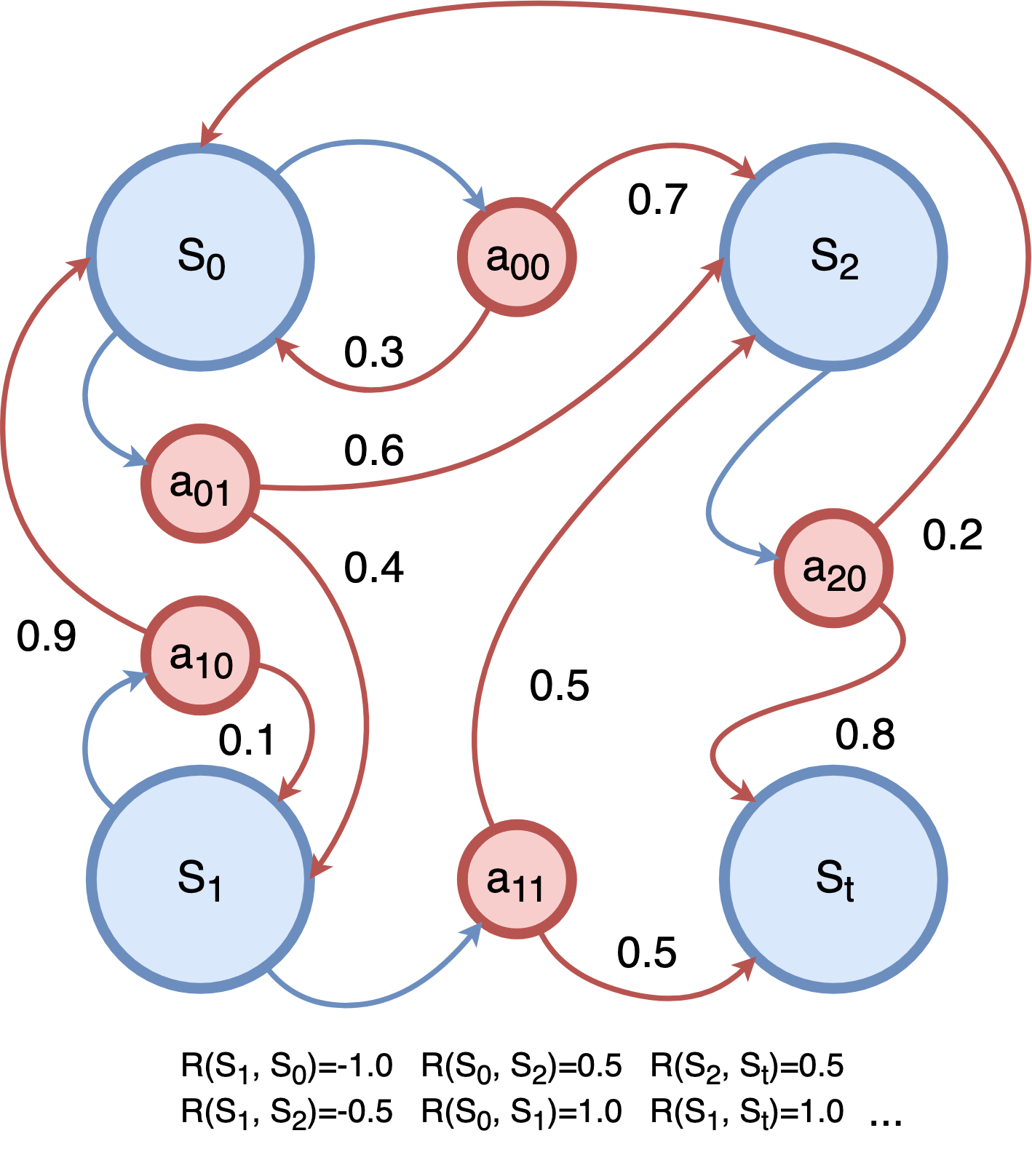
在Q-learning中，我们有一个智能体（Agent）和一个环境（Environment）。智能体可以在环境中执行动作，并从环境中获取奖励作为反馈。智能体的目标是通过与环境的交互来学习如何做出最优的动作，以最大化未来的累积奖励。

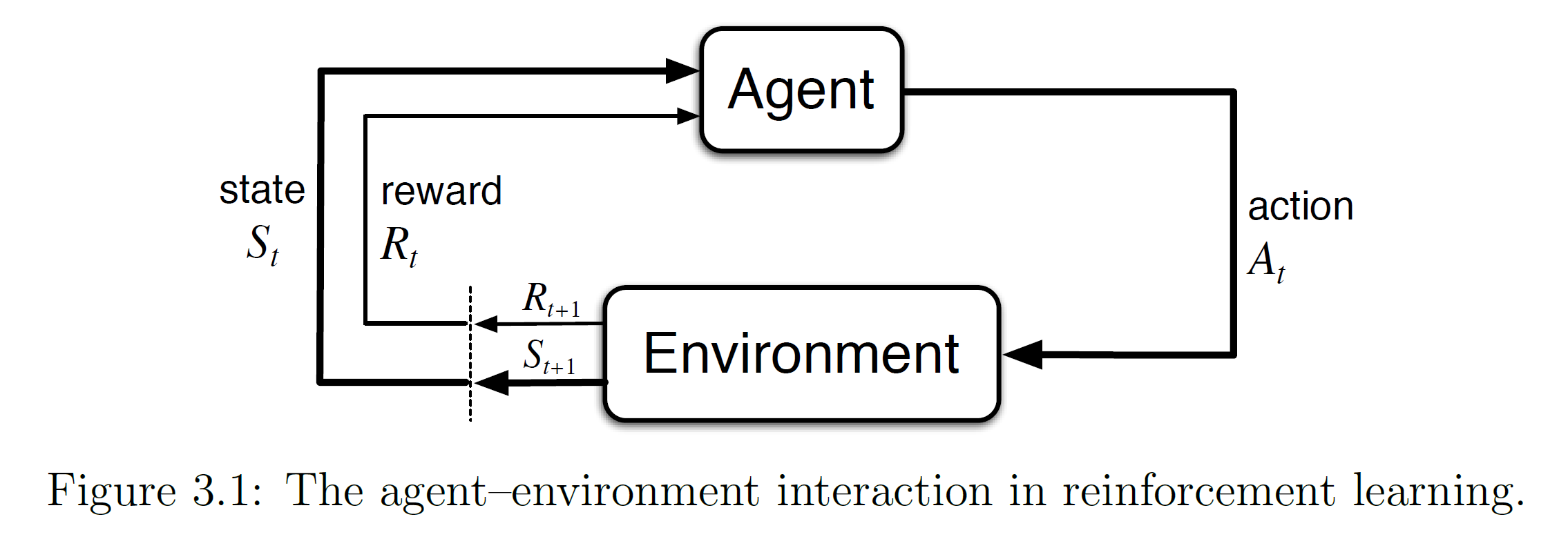
  （图源：马尔可夫决策过程图册_百度百科）

在Q-learning中，我们使用一个Q值表（Q-table）来存储智能体在每个状态下采取不同动作的Q值。Q值表示在特定状态下采取某个动作的预期累积奖励。智能体通过不断地与环境交互和更新Q值表来学习最优策略。

2. 代码思路

在我们接下来的代码中，我们使用Q-learning算法来训练智能体在一个迷宫环境中找到从起始点到目标点的最优路径。过程如下：

  1. 初始化一个迷宫地图，地图中包含可通行区域和障碍物。
  2. 创建一个Q值表，用于存储每个状态下采取不同动作的Q值。
  3. 使用Q-learning算法进行训练。训练过程包括多个episode，每个episode都是从起始点到目标点的一次尝试。
  4. 在每个episode中，智能体根据当前的Q值表选择一个动作，并在环境中执行。执行完动作后，智能体会根据环境的反馈（奖励）更新Q值表。
  5. 智能体通过不断地与环境交互和更新Q值表来学习到越来越准确的Q值，从而找到一条从起始点到目标点的最优路径。
  6. 最终，智能体学习到的最优策略就是一条从起始点到目标点的最优路径。

在代码中，我们使用了一个Agent类来表示智能体，定义了智能体的状态和动作，并实现了Q-learning算法。在训练过程中，智能体根据当前的Q值表和一个epsilon-greedy策略来选择动作。epsilon-greedy策略是一种用于在探索和开发之间进行权衡的策略，在训练初期会更多地进行探索（随机选择），以便发现新的路径，随着训练的进行，智能体会逐渐减少探索的概率，更多地利用学到的知识（选择奖励最大的action）。

最后，我们训练完智能体后，调用run_maze函数来让智能体按照学到的最优策略在迷宫中执行，并通过pygame进行可视化展示。这样，我们可以看到智能体是如何根据学到的知识在迷宫中找到最优路径的。

PS：注意，设置环境的反馈奖励来更新Q值表是一个十分关键的部分。

以迷宫为例，如果我们只设置AI每走1步就要扣1分，为了不扣分，那么它就不会走（理论上）

但是我们还规定了，只要你走不到终点，你就要选一个方向一直走。撞到墙，就扣100分。

这样，AI只有尽早地走到终点，不撞墙才是最明智的选择。

3. 实现代码

代码除了在控制台做可视化，还额外使用了pygame进行可视化，所以如果download到自己电脑上跑还可以看到窗口效果。

import numpy as np
import random
import pygame
import time
import os

"""
如果能够在自己电脑跑，还可以通过pygame看到窗口效果！
最近开始学DQN啦，希望有同窗大佬能带我一起讨论。
个人主页: https://blog.csdn.net/HYY_2000
"""
num_episodes = 2000  # 迭代次数
epsilon = 0.1  # 随机率
learning_rate = 0.1  # 学习率
discount_factor = 0.9

# 5 * 5
# maze = np.array([
#     [1, 1, 1, 1, 1],
#     [1, 0, 0, 0, 1],
#     [1, 0, 1, 0, 1],
#     [1, 0, 0, 0, 1],
#     [1, 1, 1, 1, 1],
# ])
# 10 * 10
# maze = np.array([
#     [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
#     [1, 0, 1, 0, 0, 1, 0, 0, 0, 1],
#     [1, 0, 1, 0, 1, 0, 0, 1, 1, 1],
#     [1, 0, 0, 0, 0, 0, 1, 0, 0, 1],
#     [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
#     [1, 0, 1, 0, 0, 0, 1, 1, 0, 1],
#     [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
#     [1, 0, 1, 0, 0, 0, 0, 1, 1, 1],
#     [1, 0, 1, 0, 0, 1, 0, 0, 0, 1],
#     [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
# ])
maze = np.array([
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 0, 1, 0, 0, 1, 0, 0, 0, 1],
    [1, 0, 1, 0, 1, 0, 0, 1, 1, 1],
    [1, 0, 0, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 0, 1, 1],
    [1, 0, 1, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 0, 1, 1, 1, 0, 0, 1],
    [1, 0, 0, 0, 0, 0, 0, 1, 1, 1],
    [1, 0, 1, 0, 0, 1, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
])


# 清空控制台输出
def clear_console():
    if os.name == 'nt':  # Windows系统
        os.system('cls')
    else:  # 其他系统（如Linux、macOS等）
        os.system('clear')


# 迷宫尺寸
maze_height, maze_width = maze.shape

init_position = {"x": 1, "y": 1}
end_position = {"x": maze_height - 2, "y": maze_width-2}

# AI智能体
class Agent:
    def __init__(self, state, actions):
        self.state = state
        self.actions = actions

    def choose_action(self, epsilon):
        if np.random.uniform(0, 1) < epsilon:
            return np.random.choice(self.actions)
        else:
            return np.argmax(Q_table[self.state[0], self.state[1], :])

    def update_state(self, new_state):
        self.state = new_state

# 创建迷宫界面
def draw_maze():
    for row in range(maze_height):
        for col in range(maze_width):
            color = (255, 255, 255) if maze[row, col] == 0 else (0, 0, 0)
            pygame.draw.rect(screen, color, (col * cell_size,
                             row * cell_size, cell_size, cell_size))

# 在迷宫中绘制AI智能体
def draw_agent(agent):
    row, col = agent.state
    pygame.draw.circle(screen, (255, 0, 0), (col * cell_size + cell_size //
                       2, row * cell_size + cell_size // 2), cell_size // 3)

# 控制台的绘制
def draw_agent_console(agent):
    row, col = agent.state
    maze_with_agent = maze.copy()
    maze_with_agent[row, col] = 2  # 用数字2表示智能体在迷宫中的位置
    for row in range(maze_height):
        for col in range(maze_width):
            char = "#" if maze_with_agent[row, col] == 1 else "A" if maze_with_agent[row, col] == 2 else " "
            print(char, end=" ")
        print()
        
def show_all():
    # 展示pygame的
    draw_maze()
    draw_agent(agent)
    # 展示控制台的
    clear_console()
    draw_agent_console(agent)


# 更新AI智能体在迷宫中的位置
def update_agent(agent, action):
    row, col = agent.state
    if action == 0:  # 上
        row = max(row - 1, 0)
    elif action == 1:  # 下
        row = min(row + 1, maze_height - 1)
    elif action == 2:  # 左
        col = max(col - 1, 0)
    else:  # 右
        col = min(col + 1, maze_width - 1)
    new_state = (row, col)
    return new_state

# 不同的数字表示的方位
def getChinesefromNum(action):
    action_dict = {0: "上", 1: "下", 2: "左", 3: "右"}
    return action_dict.get(action, "")

# 运行AI智能体在迷宫中的最优路径
def run_maze(agent):
    agent.state = (init_position["x"], init_position["y"])  # 初始化智能体的状态为起始点
    screen.fill((0, 0, 0))
    pygame.time.delay(500)

    while agent.state != (end_position["x"], end_position["y"]):  # 智能体到达目标点结束
        action = np.argmax(
            Q_table[agent.state[0], agent.state[1], :])  # 根据Q值表选择最优动作
        new_state = update_agent(agent, action)
        show_all()
        pygame.display.flip()
        time.sleep(0.5)
        agent.update_state(new_state)
    # 结束了之后最后画一次
    show_all()
    time.sleep(0.5)


# 初始化Q值表
Q_table = np.zeros((maze_height, maze_width, 4))

# Q-Learning算法
def q_learning(agent, num_episodes, epsilon, learning_rate, discount_factor):
    global visualize
    for episode in range(num_episodes):
        agent.state = (init_position["x"], init_position["y"])  # 初始化智能体的状态为起始点
        score = 0
        steps = 0
        path = []
        while agent.state != (end_position["x"], end_position["y"]):  # 智能体到达目标点结束
            action = agent.choose_action(epsilon)
            new_state = update_agent(agent, action)

            path.append(getChinesefromNum(action))

            # 如果设置成-5，那么相比撞墙，他不会选择绕路绕5格以上的路（惩罚5以上）。
            # reward = -1 if maze[new_state] == 0 else -5  # 根据新状态更新奖励

            reward = -1 if maze[new_state] == 0 else -100  # 根据新状态更新奖励

            # 陷入局部最优
            # distance_to_goal = abs(new_state[0] - (maze_height - 1)) + abs(new_state[1] - (maze_width - 1))
            # reward = -distance_to_goal if maze[new_state] == 0 else -999999999999999  # 根据新状态更新奖励

            # reward = (0 - distance_to_goal / (maze_height + maze_width)) if maze[new_state] == 0 else -999  # 根据新状态更新奖励

            Q_table[agent.state[0], agent.state[1], action] += learning_rate * \
                (reward + discount_factor *
                 np.max(Q_table[new_state]) - Q_table[agent.state[0], agent.state[1], action])
            agent.update_state(new_state)
            score += reward
            steps += 1

        # 输出当前的episode和最佳路径长度
        best_path_length = int(-score / 5)
        if episode % 10 == 0:
            print(f"重复次数: {episode}, 路径长度: {steps}")
            print(f"移动路径: {path}")


# Pygame初始化
pygame.init()
cell_size = 40
screen = pygame.display.set_mode(
    (maze_width * cell_size, maze_height * cell_size))
pygame.display.set_caption("Maze")

# 定义智能体
agent = Agent((1, 1), [0, 1, 2, 3])

# 运行Q-Learning算法
q_learning(agent, num_episodes, epsilon, learning_rate, discount_factor)

run_maze(agent)

# 关闭Pygame
pygame.quit()

这个程序有输出迭代过程中AI选择了哪些方向，执行后观察输出，可以看到训练轮次为0时，AI随机选择是需要上百步（大概450步）才能走到终点的。

训练到几十步，有可能AI会在某个逼仄的小角落因为怕撞墙（惩罚大）而来回踱步。因为初期随机的可能性更大可能会导致撞墙，所以导致AI不敢再去走没有走过的路，探索的过程中因为有更大的概率撞墙，所以它宁愿会选择来回踱步这种确保更轻的扣分方式。

但是训练到后面，可以看到AI会逐渐走向最近的道路。

最后的实现效果如下：

有个彩蛋，为什么我们要给撞墙设置-100分呢?我之前尝试给撞墙设置-5分，这个时候训练成熟的AI发现，相比我要绕路走额外的10步（扣10分），显然从右下角撞墙过去是更好的选择，这时候它反而会选择直接趟过黑色区域。（其实可以走黑色区域，也算是游戏bug吧哈哈）

总结：Q-learning是一种基于强化学习的算法，用于训练智能体在与环境交互的过程中学习最优策略，通过不断地更新Q值表来实现这一目标。在迷宫问题中，Q-learning可以帮助智能体找到从起始点到目标点的最优路径。

4. 与动态规划关系

这里插播一下学习Q-table的感受，不知道各位有没从Q-table身上看到一点动态规划中dp数组的影子，他们的表达方式是很相似的。（虽然还是有点区别。）

  1. 共同点：

    • 存储值函数：在动态规划中，dp数组用于存储子问题的最优解或累积奖励。在Q-learning中，Q值表用于存储智能体在每个状态和动作组合下的累积奖励预期（Q值）。
    • 状态转移更新：在动态规划中，通过递推关系式将子问题的解更新到更大规模的问题。在Q-learning中，通过采取动作并观察环境反馈（奖励和下一个状态），然后根据更新规则更新Q值表。

  2. 区别：

    • 概念不同：动态规划通常用于优化问题，它在每个阶段的最优解之间存在重叠子问题。而Q-learning是强化学习的一种形式，主要用于在不完全可知环境下训练智能体来制定最优策略。
    • 更新方式：动态规划是自底向上的，通过解决较小子问题来逐步解决大问题。Q-learning则是通过不断的试错和交互来更新Q值表，不需要先知道所有状态之间的转移概率和奖励。
    • 存储内容：动态规划的dp数组通常存储子问题的最优解值。而Q值表存储智能体在每个状态和动作组合下的预期累积奖励。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/799704.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

小程序轮播图的两种后台方式(JSP)--【浅入深出系列009】

小程序轮播图的两种后台方式(JSP)--【浅入深出系列009】

微信目录集链接在此&#xff1a; 详细解析黑马微信小程序视频–【思维导图知识范围】难度★✰✰✰✰ 不会导入/打开小程序的看这里&#xff1a;参考 让别人的小程序长成自己的样子-更换window上下颜色–【浅入深出系列001】 文章目录 本系列校训学习资源的选择啥是轮播图轮播…
阅读更多...
Retrospectives on the Embodied AI Workshop(嵌入式人工智能研讨会回顾) 论文阅读

Retrospectives on the Embodied AI Workshop(嵌入式人工智能研讨会回顾) 论文阅读

论文信息 题目&#xff1a;Retrospectives on the Embodied AI Workshop 作者&#xff1a;Matt Deitke, Dhruv Batra, Yonatan Bisk 来源&#xff1a;arXiv 论文地址&#xff1a;https://arxiv.org/pdf/2210.06849 Abstract 我们的分析重点关注 CVPR Embodied AI Workshop 上…
阅读更多...
一个开源的文件存储软件Filehub，不限速防和谐

一个开源的文件存储软件Filehub，不限速防和谐

FileHub介绍 一个基于Github开发的文件存储软件&#xff0c;美其名曰&#xff1a;FileHub&#xff0c;可存万物&#xff0c;而且绝不和谐任何文件。类似于百度云盘的功能&#xff0c;但是功能上肯定达不到百度云盘的效果&#xff0c;但是基本功能还是有的&#xff1a;例如登录注…
阅读更多...
如何实现高效的动态鉴权

如何实现高效的动态鉴权

一、概述 Spring Security 是 Spring 框架内高度可定制化的安全框架&#xff0c;也是 Spring 应用的标准安全框架&#xff0c;提供了包括认证和鉴权在内的两大部分。其高度集成于 Spring 框架&#xff0c;无需引入第三方扩展模块&#xff0c;可以避 免大量的数据接口适配问题…
阅读更多...
如何使用Git上传代码到GitHub简单教程

如何使用Git上传代码到GitHub简单教程

学习笔记 1&#xff1a;Github创建自己的一个repositories 2&#xff1a;随便给仓库取个名字 3&#xff1a;接下来&#xff0c;打开git 4&#xff1a;通过 cd 你的本地文件路径 &#xff0c;进入到该路径下 5&#xff1a;初始化项目&#xff0c;在目录下面运行完该代码后会有…
阅读更多...
Linux6.16 Docker consul的容器服务更新与发现

Linux6.16 Docker consul的容器服务更新与发现

文章目录 计算机系统5G云计算第四章 LINUX Docker consul的容器服务更新与发现一、consul 概述1.什么是服务注册与发现2.什么是consul 二、consul 部署1.consul服务器2.registrator服务器3.consul-template4.consul 多节点 计算机系统 5G云计算 第四章 LINUX Docker consul的…
阅读更多...
高压放大器在超声加工中的应用

高压放大器在超声加工中的应用

超声加工是一种非常重要的现代加工技术&#xff0c;广泛应用于材料加工、精密制造等领域。在该技术中&#xff0c;高压放大器扮演着至关重要的角色&#xff0c;可以为超声加工提供必要的信号放大和控制功能。 超声加工的原理是通过高频振动产生机械能&#xff0c;并将其传递到被…
阅读更多...
编程小白的自学笔记十二（python爬虫入门四Selenium的使用实例二）

编程小白的自学笔记十二（python爬虫入门四Selenium的使用实例二）

系列文章目录 编程小白的自学笔记十一&#xff08;python爬虫入门三Selenium的使用实例详解&#xff09; 编程小白的自学笔记十&#xff08;python爬虫入门二实例代码详解&#xff09; 编程小白的自学笔记九&#xff08;python爬虫入门代码详解&#xff09; 目录 系列文章…
阅读更多...
Jmeter性能测试配置

Jmeter性能测试配置

Jmeter检查点/断言 在上一章节中&#xff0c;我们通过调试脚本&#xff0c;通过人工验证脚本可以完成业务功能&#xff0c; 但在性能测试中&#xff0c;我们希望能通过自动验证脚本是否完成业务功能&#xff0c;在Jmeter 中我们可以通过检查点&#xff0c;也就是断言来实现自动…
阅读更多...
19.2：纸牌问题

19.2：纸牌问题

给定一个整型数组arr&#xff0c;代表数值不同的纸牌排成一条线 玩家A和玩家B依次拿走每张纸牌 规定玩家A先拿&#xff0c;玩家B后拿 但是每个玩家每次只能拿走最左或最右的纸牌 玩家A和玩家B都绝顶聪明 请返回最后获胜者的分数 方法一&#xff1a;暴力解法 自然智慧。 pack…
阅读更多...
【NLP入门教程】二十三、循环神经网络（RNN）| 小白专场

【NLP入门教程】二十三、循环神经网络（RNN）| 小白专场

本教程旨在为初学者提供一份全面而系统的NLP入门指南&#xff0c;探索NLP的核心概念、方法和技术。无论你是计算机科学的新手&#xff0c;还是对自然语言处理领域感兴趣的研究人员&#xff0c;本教程都将为你提供所需的基础知识和实用技能。 专栏地址&#xff1a;&#x1f4d5…
阅读更多...
【蓝图】p40-p43对象引用、变量有效性、实现键盘控制物体自转、简单点名系统

【蓝图】p40-p43对象引用、变量有效性、实现键盘控制物体自转、简单点名系统

p40-p43对象引用、变量有效性、实现键盘控制物体自转、简单点名系统 p40对象引用、变量有效性p41实现键盘控制物体自转创建bool值控制旋转实现通过键盘控制自转 p42p43简单点名系统Get All Actors Of Class&#xff08;获得场景中所有该类的actor演员&#xff09;getFor Each L…
阅读更多...
TEE GP(Global Platform)安全认证产品

TEE GP(Global Platform)安全认证产品

TEE之GP(Global Platform)认证汇总 一、安全认证产品介绍 选择SECURITY和TEE SECURITY&#xff0c;然后SEARCH&#xff0c;可以看到TEE对应的安全认证产品。 二、HUAWEI ITRUSTEE V3.0 ON KIRIN 980 三、SAMSUNG TEEGRIS V4.1 参考&#xff1a; GlobalPlatform Certification…
阅读更多...
【linux】暗夜精灵9自动升级BIOS后，无法进入双系统

【linux】暗夜精灵9自动升级BIOS后，无法进入双系统

1、问题描述 暗夜精灵9自动升级BIOS后，无法进入双系统，甚至没有“多重引导菜单” 2、解决方法 1）进入BIOS 惠普暗夜精灵9进入BIOS的按键是F10 2）设置启动项 需要设置三处 功能键延时：5秒 安全启动模式：关闭 UEFI模式下的开机顺序：ubuntu3）设置显卡切换 如果NVIDIA…
阅读更多...
TCL(Tool Command Language)学习（三）-----字符串操作

TCL(Tool Command Language)学习（三）-----字符串操作

一、比较 &#xff1a; string compare 格式 &#xff1a; string compare ?-nocase? ?-length int? string1 string2 把字符串 string1 和字符串 string2 进行比较 &#xff0c;返回值为 -1、0或 1 &#xff0c;分别对应 string1 小于、等于或大于string2。如果有 -len…
阅读更多...
全球百年品牌，最高已改变25次

全球百年品牌，最高已改变25次

摘要&#xff1a;今天&#xff0c;我们看到的那些持久的公司并不是真正持续了100年的公司。在100年的时间里,他们改变了25次、5次或4次,如果不改变,他们就无法生存。 近期市场调研中&#xff0c;许战海咨询发现国内市场已经进入无限内卷的竞争阶段。如何在内卷的竞争中保持可持…
阅读更多...
Android OpenGL ES Camera2 实现实时抠图效果

Android OpenGL ES Camera2 实现实时抠图效果

前面文章人像抠图 + OpenGL ES 还能这样玩？没想到吧，我们介绍了利用人像抠图算法生成的 mask 图，然后结合 OpenGL 可以产生一些有趣的效果。 抠图技术应用很广泛，比如很多手机的相机自带“人像留色”滤镜：人体区域保留彩色，人体区域之外灰度化。所以人像留色的关键技术在…
阅读更多...
Unity下如何实现低延迟的全景RTMP|RTSP流渲染

Unity下如何实现低延迟的全景RTMP|RTSP流渲染

技术背景 Unity3D可以用于创建各种类型的的应用程序&#xff0c;包括虚拟现实、培训模拟器等。以下是一些可以使用Unity3D全景播放的场景&#xff1a; 虚拟现实体验&#xff1a;全景视频可以用来创建逼真的虚拟环境&#xff0c;使用户能够感受到身临其境的感觉&#xff1b;培…
阅读更多...
Spring中的Bean配置

Spring中的Bean配置

bean配置 基础配置 别名配置 作用范围配置 1、为什么bean会默认为单例&#xff1f; 如果不为单例&#xff0c;则每一次调用bean&#xff0c;Spring的bean容器中&#xff0c;会出现多个该类的对象&#xff0c;这会造成容器的冗余。 2、适合交给容器进行管理的bean 表现层对象…
阅读更多...
Ansys Zemax | 确保自由曲面设计的可制造性

Ansys Zemax | 确保自由曲面设计的可制造性

本文专门介绍使用单点金刚石车床加工自由曲面的主要可制造性参数&#xff0c;解释了可制造性参数如何与仪器参数相关联&#xff0c;并展示了如何在 OpticStudio 中检查和控制这些可制造性参数。此外&#xff0c;还解释了如何处理其考察区域外的自由曲面的行为。例如&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023