每天一道C语言编程（递归：斐波那契数，母牛的故事）

news2024/11/19 3:39:15

递归的条件

递归函数必须有一个可直接退出的条件，否则会进入无限递归，例如

#include<stdio.h>
void f(int n)
{
	if(n<0)
		return;
	f(n-1);
	printf("%d ",n);
}

int main()
{
	int n=5;
	f(n);
	return 0;
	
}

//递归的出口
if(n<0)
return;

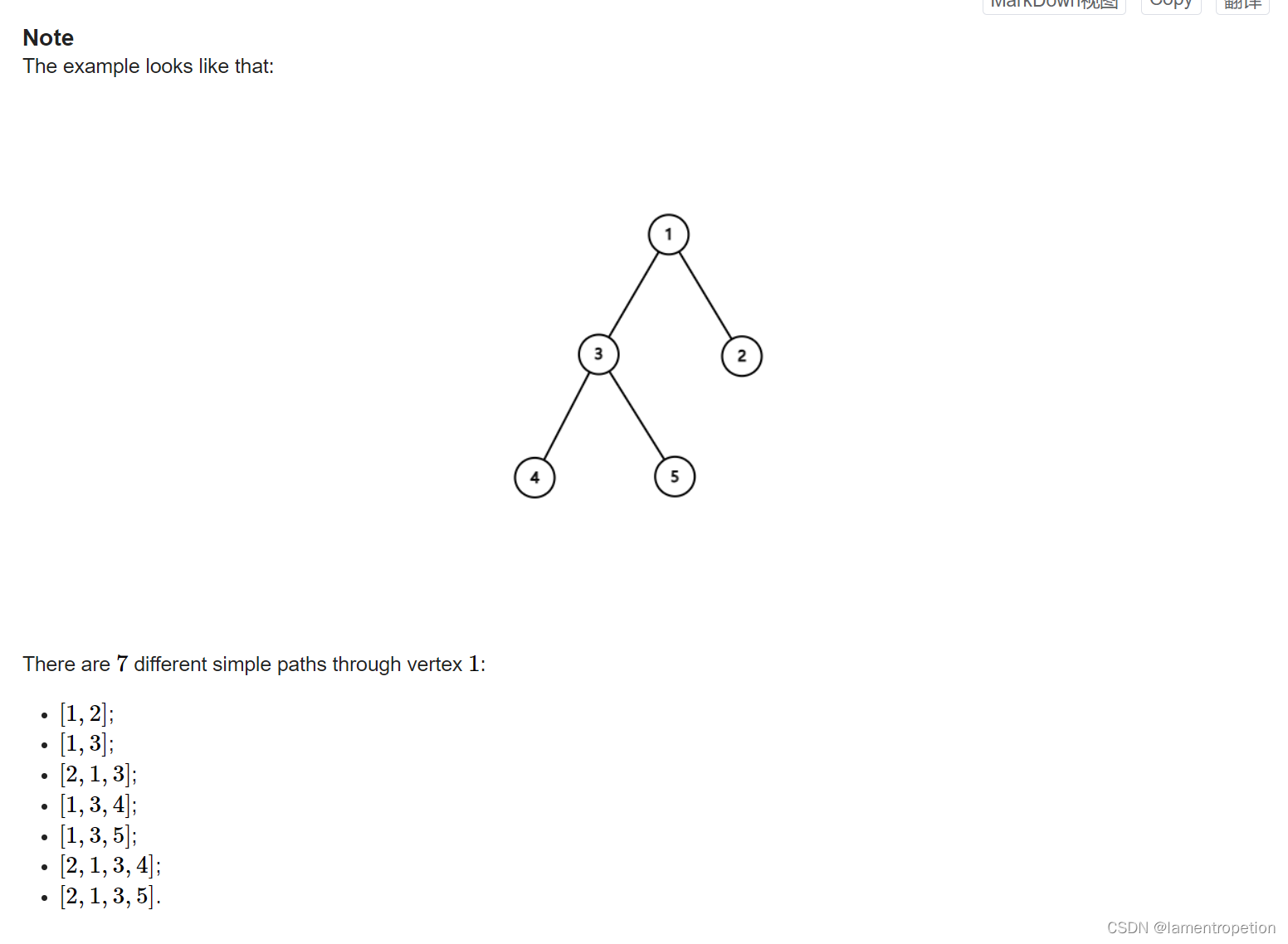
调用的过程如图所示

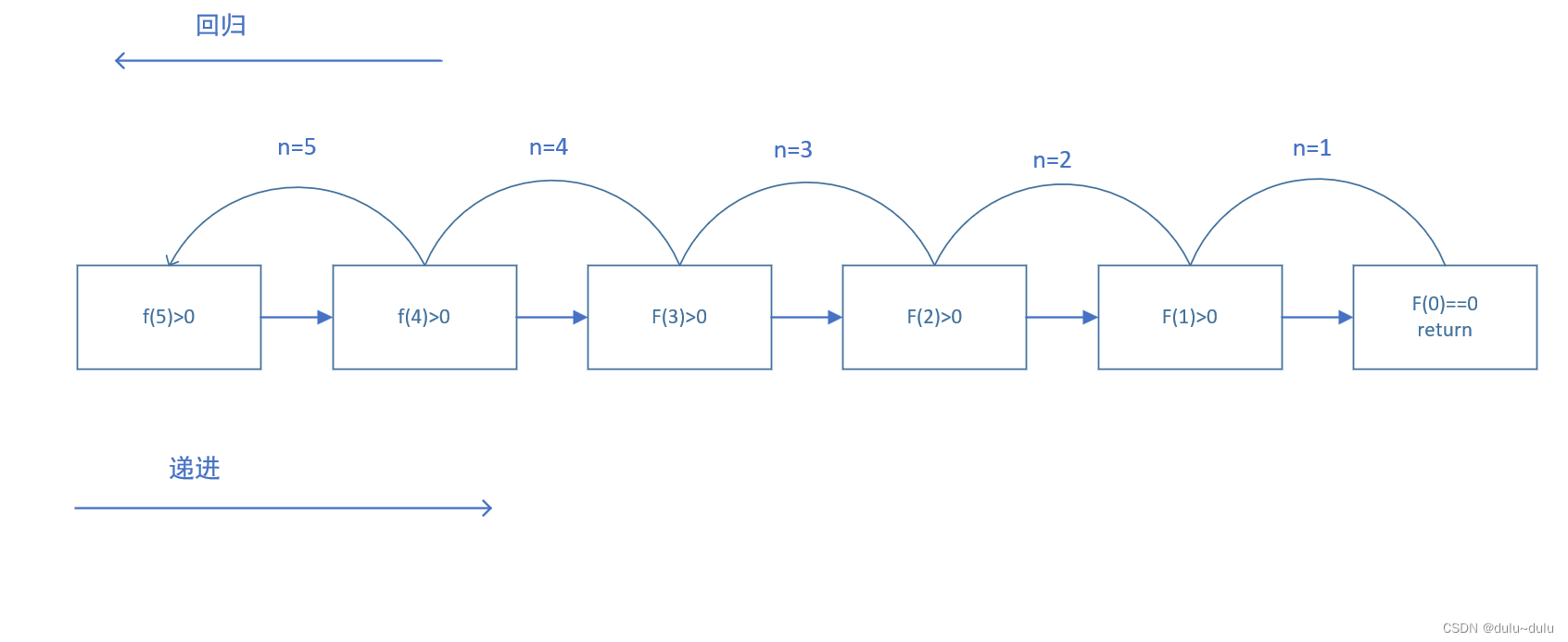
注：

• 递归调用时，函数的栈内存的变化如下图所示。可见，随着递归函数的层层深入，栈空间逐渐往下增长，如果递归的层次太深，很容易把栈内存耗光。
•层层递进时，问题的规模会随之减小，减小到可直接退出的条件时，函数开始层层回归。

接下来看几个练习

题目描述

有一头母牛，它每年年初生一头小母牛。每头小母牛从第四个年头开始，每年年初也生一头小母牛。请编程实现在第n年的时候，共有多少头母牛？

输入格式

输入数据由多个测试实例组成，每个测试实例占一行，包括一个整数n(0<n<55)，n的含义如题目中描述。
n=0表示输入数据的结束，不做处理。

输出格式

对于每个测试实例，输出在第n年的时候母牛的数量。
每个输出占一行。

样例输入

样例输出

2
4
6

根据每四年生一头小母牛，可列出表格：

年份	1	2	3	4	5	6	7	8	9
母牛数量	1	2	3	4	6	9	13	19	28

观察规律得到

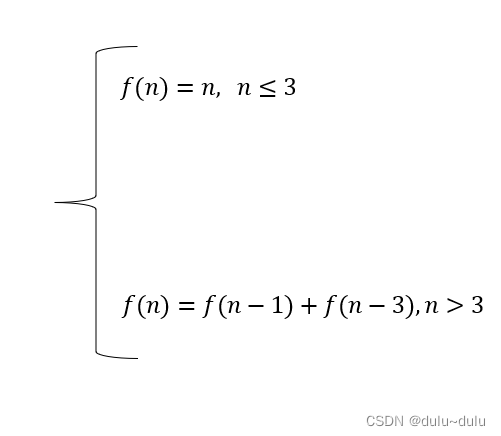
代码如下

# include<stdio.h>
 
int fun(int n)
{
    if(n<=3) return n;
    else return fun(n-1)+fun(n-3);
}
int main()
{
    int n;
    while(scanf("%d",&n) && n)
/*
如果n不为0，则进入循环，也可以写为
while(treue)
{
    scanf("%d",&n);
    if(n==0)
        break;
}
*/
        printf("%d\n",fun(n));
 
    return 0;
}

类似于斐波那契数

1、1、2、3、5、8、13、21、34 ……
斐波那契数列的规律是，除了最开头的两项之外，其余任意一项的值等于前两项之和。而开头的两项都是1。用数学公式表达是：

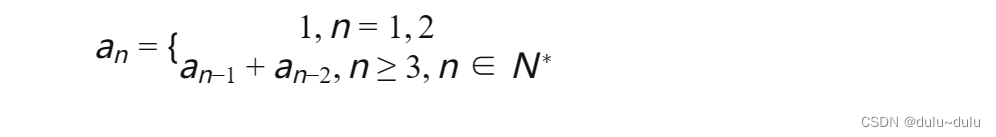
#include <stdio.h>

int fibonacci(int num)
{
    // 第1和第2个斐波那契数不需要经过任何计算，规定都是1
    if(num == 1 || num == 2)
        return 1;
    
    // 第N个斐波那契数，等于第N-1个和第N-2个斐波那契数之和
    return (fibonacci(num-1) + fibonacci(num-2));
}


int main(void)
{
  
    int num;
    scanf("%d", &num); 
    printf("第 %d 个斐波那契数是: %d\n", num, fibonacci(num));
    return 0;
}

编写一个函数,给出底数x和幂函数 N，计算 $x^{N}$ ，例如

float ans1 = myPower(4, 2);     // 4的2次方
float ans2 = myPower(3.14, -2); // 3.14的-2次方

运用递归

$x^{N}$ = $x^{N-1}*x$

可得代码如下

#include<stdio.h>

 float f(float x,int n)
 {
 	if(n==0)
 		return 1;
 	else
 		return f(x,n-1)*x;
 }
 
 int main()
 {
 	float x;
 	int n;
 	scanf("%f %d",&x,&n);
 	if(x==0)
 		printf("0");
 		
    //除0之外的任何数的0次幂=1 
	else if(x != 0 && n == 0)
		printf("%f^%d = 1\n", x, n);
	
	//负整数次幂 
	else if(n<0)
	{
		n*=-1;
		printf("%f^-%d=%.6f",x,n,1/f(x,n));
	}
	
	//正整数次幂 
	 else
    {
        printf("%f^%d = %.6f\n", x, n, f(x, n));
    }
	return 0;
 }

结果示例