http://oj.daimayuan.top/course/8/problem/400

题意：

 

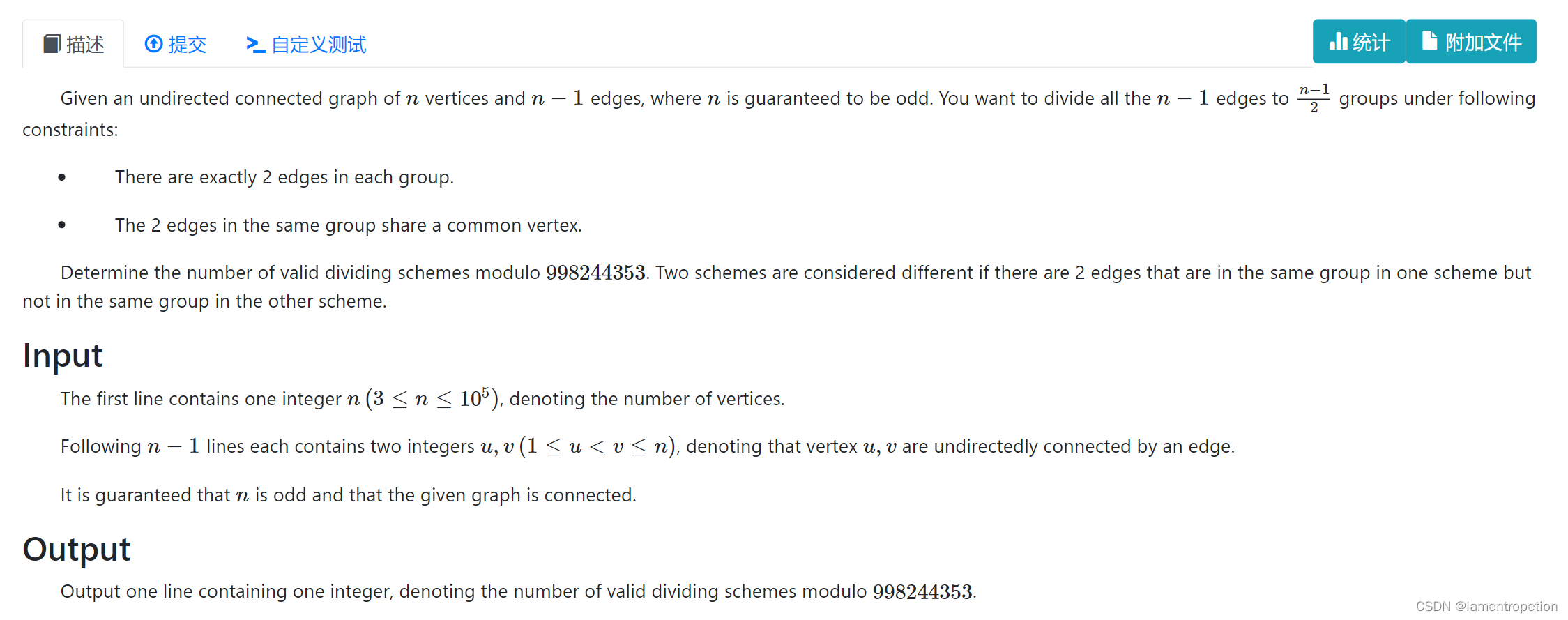
思路：

求方案数，考虑组合数学

手摸一下样例发现，对于一棵子树，若边数为偶数，那么可以内部匹配，但是如果边数为奇数，那么就一定需要u和fa那条边和子树的边匹配

考虑乘法原理

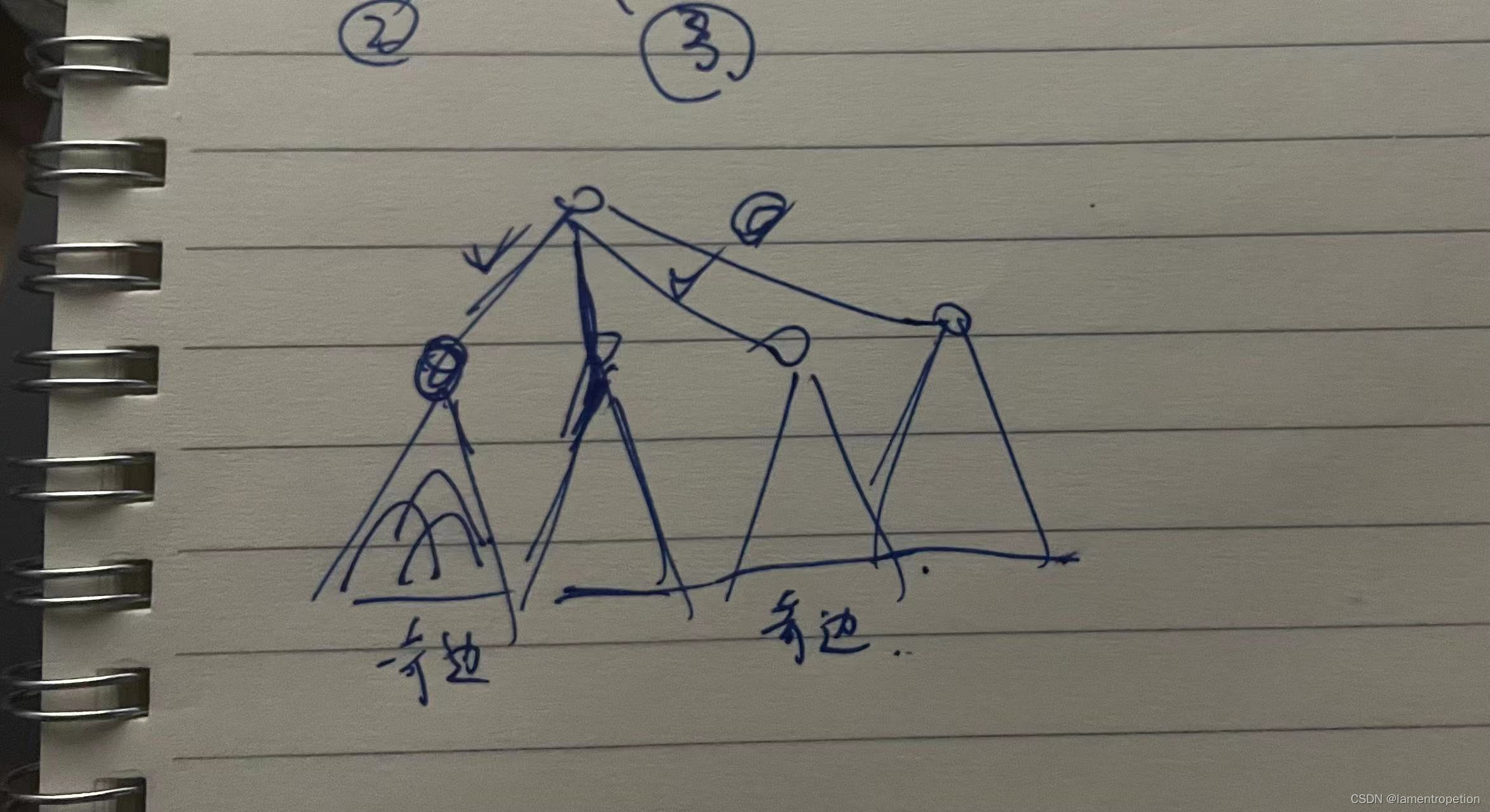
将多出来的边进行匹配

如果边数还为奇数，那么就和u和fa这条边匹配

若多出来K条边，由乘法原理知道，方案数为(K-1)*(K-3)*....

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=1e6+10;
const int mxv=1e6+10;
const int mod=998244353;

vector<int> G[mxn];

int N,u,v;
int ans=1;
int sz[mxn];

void dfs(int u,int fa){
	int cnt=0;
	sz[u]=1;
	for(auto v:G[u]){
		if(v==fa) continue;
		dfs(v,u);
		sz[u]+=sz[v];
		if(sz[v]&1) cnt++;
	}
	if(cnt&1) cnt++;
	for(int i=cnt-1;i>=0;i-=2){
		ans=ans*i%mod;
	}
}
void solve(){
	cin>>N;
	for(int i=1;i<=N-1;i++){
		cin>>u>>v;
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dfs(1,0);
	cout<<ans%mod<<'\n';
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int __=1;//cin>>__;
	while(__--)solve();return 0;
}