找到一个非常棒的教程：本科生自学微分流形有哪些资料推荐？ - 知乎

应该是目前微积分的终极答案了（非数学系）

 

 

 

首先，这个函数具有线性结构。所以他是属于V*的。 之前我倒没想过这个问题，以为所有的泛函都是V*,没考虑过线性问题。而且既然是线性，那么如果是一维的，就应该是y=kx。必须是这个形式才行吧。

 这一段证明过程看似普通，但其实要很好的理解里面的深意。

 所以V*里的元素就是alpha,而alpha可以由一组基线性组合而成。重点来了，它的系数是这个alpha作用在ei上。不过我感觉它中间推导有点问题，不过结果是对的。这个结论挺奇妙的，线性泛函的基是每个基坐标的alpha的线性组合。它的系数是alpha作用在ei上。这个要好好理解，按理说它取到的是ei的坐标，就是1.当然，我们可以感受到，如果坐标是其他值，也是可以的，只要复合约定就行。

重点看这个注解，首先是内积的引入，这个好理解，一个取坐标的操作是可以看成一个向量和另个一个基的内积。 后面这个可能不太好理解，但其实只要举个例子就行：

alpha e1=(a1alpha1 +a2alpha2)e1 = a1 alpha1 e1 + 0 = a1 alpha1(e1) = a1

然后，v=<a,v>ei  说明a是它上面的线性函数，而反过来alpha = <>alphai, 则说明ei是V*上的线性函数。确实美妙。

 这里其实是用ei的基来组成一个新的基e拔。以为内变换的雅克比矩阵的行列式不为0，所以是一个可逆变换。这个笔记里笔误挺多的啊。alphai拔明显要和alphai对应才对。

证明过程写的也有点问题，我自己在纸上写是对的，但这个求和符号我还得再看看

这样就对了。所以是可逆的。

 

这个思路很好。

 这里的证明倒没有出任何问题。

这里其实并没有那么好理解，要注意，得到f和后面的表达式后，因为要说明后面是f的一组基，首先得到他们是线性无关的，而且按照我们前面对偶基的写法，我们也能慢慢理解

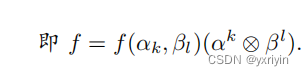
这就是爱婴斯坦求和公式的妙处吧。

 张量积有了，不知道张量本身的定义有没有呢？

话说张量积的乘法真的是乘法吗，我继续看看。

后面这个结论主要可以类比：f=f(V空间的基)V*空间的基。

这里要注意：(v1, v2),  (w1, w2, w3)那么它的基有6个：(v1,w1),(v1,w2),(v1,w3), (v2,w1),(v2,w2),(v2,w3)

直积不一样：会是(v1,0),(v2,0), (0,w1), (0,w2), (0,w3)

 

 

这里作者说的也不清不楚的。直接说我的理解把，如果e为原始基，a为变换后的基。那么（2）

f拔就是原始张量坐标，f就是新的张量坐标。

 

这里我要思考的是(1,1)型张量的分量表示为什么是矩阵。F是老基下的矩阵，A是变换矩阵，那么

S=AFA^-1，这个是相似矩阵的公式。从张量去理解的话，线性变换f是L(V,V*,F), 这里参考：[前置内容] 从映射到张量 - 知乎

 这是双线性映射。

 

 这个证明其实不太好想，按照线性代数上面的教材更加简单。

首先对偶空间和原始空间的维数相同，我只要证明对偶基是线性无关即可。

所以a1e1 + a2e2 =0. 只要证明a1=a2=0即可。让他们分别作用于原始基v1,v2

可以得到a1e1v1=a1=0,同理 a2=0,得证。

自然同构的部分可以看成本身。

 

这里可能会有点困惑，V上的泛函，对于具体的v*而言，可以取v和输入的内积。这样得到一个F。

按理说，v*应该和v本身没有直接关系。我尝试推导下：v=a1x + a2y,基是x和y，那么对应的对偶基就是e1(x) = 1  e2(y) = 1, 记得前面的推导过程：（记住结论就行） 

v*(v)=v*(x)e1 + v*(y)e2

从这个角度将，v*和v，虽然都是v，但是应该不一定是有什么联系。

不过确实可以继续思考，如果v的基是(x,y),坐标是(a,b),那么对偶空间上有个向量，是m e1 + n e2

那么m e1 +n e2(ax + by), 最终就是 ma + nb, 这其实就是内积啊。 

 确实，从内积的角度去理解，更加具体，不然太抽象了，也记不住啊。

原来是诱导出来的，所以两个v可以是同一个含义，因为我们建立了这样的一一映射。再回去理解

V x V* ->F  其实就是内积吧。

 

这里其实可以看出来，（1,1）型张量就是矩阵，为什么呢，内积换成矩阵就是行向量和列向量的乘积。那么对于一个矩阵，你左乘一个行向量，右乘一个列向量，那么就是一个数了。所以这里注意，对偶矢量就是行向量，而矢量我们用列向量。

 这个解释也很不错。