【MATLAB】ILOSpsi制导率的代码解析

news2024/9/23 3:19:46

ILOSpsi制导率的代码解析

这里记录一下关于fossen的MMS工具箱中，关于ILOSpsi制导率的代码解析内容，结合fossen的marine carft hydrodynamics and motion control这本书来参考看

文章目录

  • ILOSpsi制导率的代码解析
  • 前言
  • 一、代码全文
  • 二、内容解析
    • 1.persistent变量
    • 2.初始化
    • 3.读取下一个航路点
    • 4.计算路径的切向角
  • 总结

前言

提示：这里可以添加本文要记录的大概内容：

相较于传统的制导率，ILOS或积分LOS可用于消除由运动学建模误差引起的x中的稳态偏移。一个典型的例子是由于飞行器的滚动和俯仰运动而忽略了运动耦合项。

提示：以下是本篇文章正文内容，下面案例可供参考

一、代码全文

function [psi_d, r_d, y_e] = ILOSpsi(x,y,Delta,kappa,h,R_switch,wpt,U,K_f)
% [psi_d, r_d, y_e] = ILOSpsi(x,y,Delta,kappa,h,R_switch,wpt,U) 
% ILOSpsi computes the desired heading angle psi_d, desired yaw rate r_d 
% and cross-track error y_e when the path is  straight lines going through 
% the waypoints (wpt.pos.x, wpt.pos.y). The desired heading angle computed 
% using the classical ILOS guidance law by Børhaug et al. (2008).
%
%    psi_d = pi_h - atan( Kp * (y_e + kappa * y_int) ),  Kp = 1/Delta
%
%    d/dt y_int = Delta * y_e / ( Delta^2 + (y_e + kappa * y_int)^2 )
%
% where pi_h is the path-tangential (azimuth) angle with respect to the 
% North axis and y_e is the cross-track error. The observer/filter for the 
% desired yaw angle psi_d is
%
%    d/dt psi_f = r_d + K_f * ssa( psi_d - psi_f ) )
%
% where the desired yaw rate r_d = d(psi_d)/dt is computed by
%
%    d/dt y_e = -U * y_e / sqrt( Delta^2 + y_e^2 )
%    r_d = -Kp * dy_e/dt / ( 1 + (Kp * y_e)^2 )   
%
% Initialization:
%   The active waypoint (xk, yk) where k = 1,2,...,n is a persistent
%   integer should be initialized to the first waypoint, k = 1, using 
%   >> clear ILOSpsi
%
% Inputs:   
%   (x,y): craft North-East positions (m)
%   Delta: positive look-ahead distance (m)
%   kappa: positive integral gain constant, Ki = kappa * Kp
%   h: sampling time (s)
%   R_switch: go to next waypoint when the along-track distance x_e 
%             is less than R_switch (m)
%   wpt.pos.x = [x1, x2,..,xn]' array of waypoints expressed in NED (m)
%   wpt.pos.y = [y1, y2,..,yn]' array of waypoints expressed in NED (m)
%   U: speed, vehicle cruise speed or time-varying measurement (m/s)
%   K_f: observer gain for desired yaw angle (typically 0.1-0-5)
%
% Feasibility citerion: 
%   The switching parameter R_switch > 0 must satisfy, R_switch < dist, 
%   where dist is the distance between the two waypoints at k and k+1:
%      dist = sqrt(  (wpt.pos.x(k+1)-wpt.pos.x(k))^2 
%                  + (wpt.pos.y(k+1)- wpt.pos.y(k))^2 );
%
% Outputs:  
%    psi_d: desired heading angle (rad)
%    r_d:   desired yaw rate (rad/s)
%    y_e:   cross-track error (m)
%
% For course control use the functions LOSchi.m and ILOSchi.m.
%
% Ref. E. Børhaug, A. Pavlov and K. Y. Pettersen (2008). Integral LOS 
% Control for Path Following of Underactuated Marine Surface Vessels in the 
% presence of Constant Ocean Currents. Proc. of the 47th IEEE Conference 
% on Decision and Control, pp. 4984–4991, Cancun, Mexico.
%  
% Author:    Thor I. Fossen
% Date:      10 June 2021
% Revisions: 26 June 2022 - use constant bearing when last wpt is reached,  
%                           bugfixes and improved documentation
%            17 Oct 2022  - added filter/observer for psi_d to avoid steps 

persistent k;      % active waypoint index (initialized by: clear ILOSpsi)持久变量标注了路点的序列
persistent xk yk;  % active waypoint (xk, yk) corresponding to integer k
persistent psi_f;  % filtered heading angle command
persistent y_int;  % integral state

%% Initialization of (xk, yk) and (xk_next, yk_next), and integral state 
if isempty(k)

    % check if R_switch is smaller than the minimum distance between the waypoints
    if R_switch > min( sqrt( diff(wpt.pos.x).^2 + diff(wpt.pos.y).^2 ) )
        error("The distances between the waypoints must be larger than R_switch");
    end

    % check input parameters
    if (R_switch < 0); error("R_switch must be larger than zero"); end
    if (Delta < 0); error("Delta must be larger than zero"); end

    y_int = 0;              % initial states
    psi_f = 0;
    k = 1;                  % set first waypoint as the active waypoint
    xk = wpt.pos.x(k);
    yk = wpt.pos.y(k);
    fprintf('Active waypoints:\n')
    fprintf('  (x%1.0f, y%1.0f) = (%.2f, %.2f) \n',k,k,xk,yk);

end

%% Read next waypoint (xk_next, yk_next) from wpt.pos 
n = length(wpt.pos.x);
if k < n                        % if there are more waypoints, read next one 
    xk_next = wpt.pos.x(k+1);  
    yk_next = wpt.pos.y(k+1);    
else                            % else, continue with last bearing
    bearing = atan2((wpt.pos.y(n)- wpt.pos.y(n-1)), (wpt.pos.x(n)-wpt.pos.x(n-1)));
    R = 1e10;
    xk_next = wpt.pos.x(n) + R * cos(bearing);
    yk_next = wpt.pos.y(n) + R * sin(bearing); 
end

%% Compute the path-tangnetial angle w.r.t. North
pi_h = atan2( (yk_next-yk), (xk_next-xk) ); 

% along-track and cross-track errors (x_e, y_e) 
x_e =  (x-xk) * cos(pi_h) + (y-yk) * sin(pi_h);
y_e = -(x-xk) * sin(pi_h) + (y-yk) * cos(pi_h);

% if the next waypoint satisfy the switching criterion, k = k + 1
d = sqrt( (xk_next-xk)^2 + (yk_next-yk)^2 );
if ( (d - x_e < R_switch) && (k < n) )
    k = k + 1;
    xk = xk_next;       % update active waypoint
    yk = yk_next; 
    fprintf('  (x%1.0f, y%1.0f) = (%.2f, %.2f) \n',k,k,xk,yk);
end

% ILOS guidance law
Kp = 1/Delta;
psi_d = psi_f;
psi_ref = pi_h - atan( Kp * (y_e + kappa * y_int) ); 

% desired yaw rate r_d
Dy_e = -U * y_e / sqrt( Delta^2 + y_e^2 );    % d/dt y_e
r_d = -Kp * Dy_e / ( 1 + (Kp * y_e)^2 );      % d/dt psi_d

% integral state: y_int[k+1]
y_int = y_int + h * Delta * y_e / ( Delta^2 + (y_e + kappa * y_int)^2 );

% observer/filter: psi_f[k+1]
psi_f = psi_f + h * ( r_d + K_f * ssa( psi_ref - psi_f ) );


end

二、内容解析

1.persistent变量

下面是持久变量的定义，持久变量会被保存在内存中，函数的持久变量不会因为函数结束调用而清零，而是会在代码运行过程中不断累计。
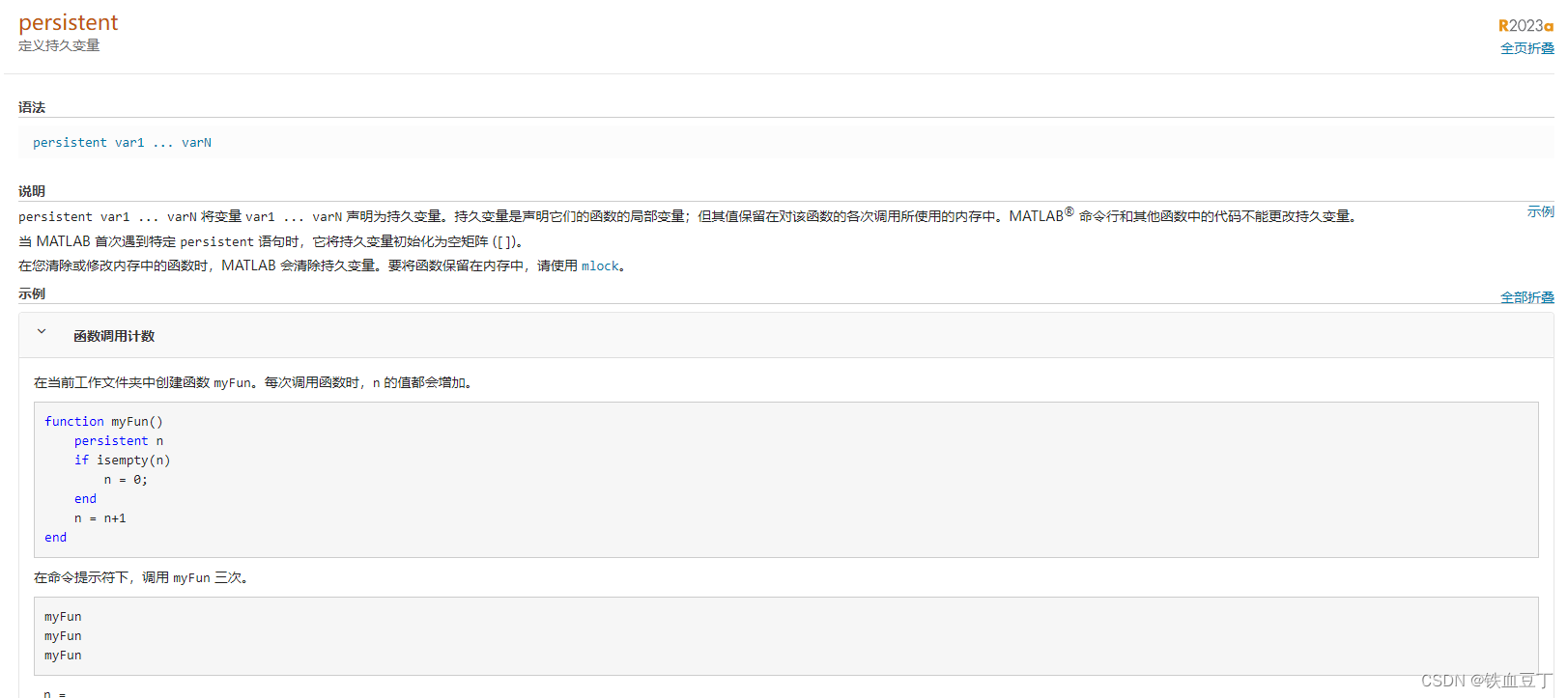
在这里插入图片描述
下面先定义了四个持久变量

persistent k;      % active waypoint index (initialized by: clear ILOSpsi) 标注了路点的序列
persistent xk yk;  % active waypoint (xk, yk) corresponding to integer k 标注了第k个路点的序列
persistent psi_f;  % filtered heading angle command 滤波后的航向角命令
persistent y_int;  % integral state 积分状态

2.初始化

代码如下（初始化部分）：

%% Initialization of (xk, yk) and (xk_next, yk_next), and integral state 
if isempty(k) % 确定数组k是否为空，若为空则进入初始化步骤

    % check if R_switch is smaller than the minimum distance between the waypoints
    % 检查一下R是否小于最小的路点间的距离
    if R_switch > min( sqrt( diff(wpt.pos.x).^2 + diff(wpt.pos.y).^2 ) )
        error("The distances between the waypoints must be larger than R_switch");% 小于航路点间的距离，说明R选取的不合适，报错
    end

    % check input parameters
    if (R_switch < 0); error("R_switch must be larger than zero"); end
    % R必须选择大于0的圆
    if (Delta < 0); error("Delta must be larger than zero"); end
	% 参数delta也必须大于0
	% 初始化状态
    y_int = 0;              % initial states
    psi_f = 0;
    k = 1;                  % set first waypoint as the active waypoint 设定第一个航路点为活跃点
    xk = wpt.pos.x(k);
    yk = wpt.pos.y(k);
    fprintf('Active waypoints:\n')
    fprintf('  (x%1.0f, y%1.0f) = (%.2f, %.2f) \n',k,k,xk,yk);

end

检查R和航路点间的距离

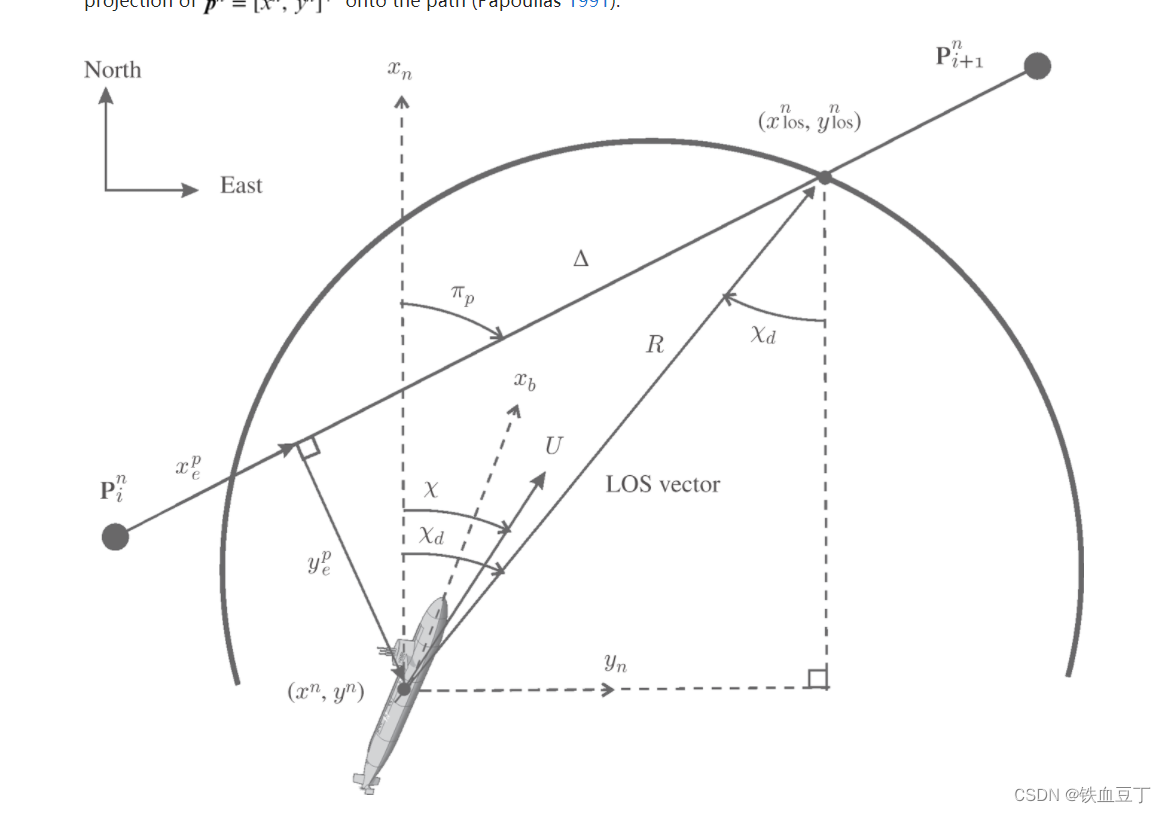
在这里插入图片描述
对于Enclosure-based LOS 的制导率来说，通过包围载体的圆的半径来确定载体和载体路径之间的距离关系。R一定要选择比行路点序列中两点间距离更大的点。

若选择的R足够大，那么圆就会和直线相交于两个端点上，那么该制导率的策略就是ye指向焦点pn

3.读取下一个航路点

%% Read next waypoint (xk_next, yk_next) from wpt.pos 
n = length(wpt.pos.x);% 返回航路点的个数
if k < n                        % if there are more waypoints, read next one 若是k小于航路点的总个数，那么继续读取下一个航路点
    xk_next = wpt.pos.x(k+1);  
    yk_next = wpt.pos.y(k+1);    
else                            % else, continue with last bearing 若是达到了航路点的尽头，那么沿着最后一个航路点的方位继续前进
    bearing = atan2((wpt.pos.y(n)- wpt.pos.y(n-1)), (wpt.pos.x(n)-wpt.pos.x(n-1)));
    R = 1e10;
    xk_next = wpt.pos.x(n) + R * cos(bearing);
    yk_next = wpt.pos.y(n) + R * sin(bearing); 
end

4.计算路径的切向角

%% Compute the path-tangnetial angle w.r.t. North
pi_h = atan2( (yk_next-yk), (xk_next-xk) ); % 求解旋转角pi_p

% along-track and cross-track errors (x_e, y_e) 求解路径坐标系下的x轴误差和y轴误差
x_e =  (x-xk) * cos(pi_h) + (y-yk) * sin(pi_h);
y_e = -(x-xk) * sin(pi_h) + (y-yk) * cos(pi_h);

% if the next waypoint satisfy the switching criterion, k = k + 1
d = sqrt( (xk_next-xk)^2 + (yk_next-yk)^2 );% 求解一下当前位置和下一点位置间的距离
if ( (d - x_e < R_switch) && (k < n) )% 若是距离delta小于圆的半径，以及k还在序列范围内
    k = k + 1;% k进一步更新
    xk = xk_next;       % update active waypoint 更新当前的目标点
    yk = yk_next; 
    fprintf('  (x%1.0f, y%1.0f) = (%.2f, %.2f) \n',k,k,xk,yk);
end

% ILOS guidance law
% 这里是引导率的核心算法处
Kp = 1/Delta;
psi_d = psi_f;
psi_ref = pi_h - atan( Kp * (y_e + kappa * y_int) ); % 制导率的公式

% desired yaw rate r_d
Dy_e = -U * y_e / sqrt( Delta^2 + y_e^2 );    % d/dt y_e
r_d = -Kp * Dy_e / ( 1 + (Kp * y_e)^2 );      % d/dt psi_d

% integral state: y_int[k+1]
y_int = y_int + h * Delta * y_e / ( Delta^2 + (y_e + kappa * y_int)^2 );

% observer/filter: psi_f[k+1]
psi_f = psi_f + h * ( r_d + K_f * ssa( psi_ref - psi_f ) );

（1）计算xe ye
根据fossen书中所讲，先求解一下 path-tangential coordinate 坐标系相对应的xe和ye误差。
先求解以下pi_p，再利用二维的坐标旋转矩阵来求解：
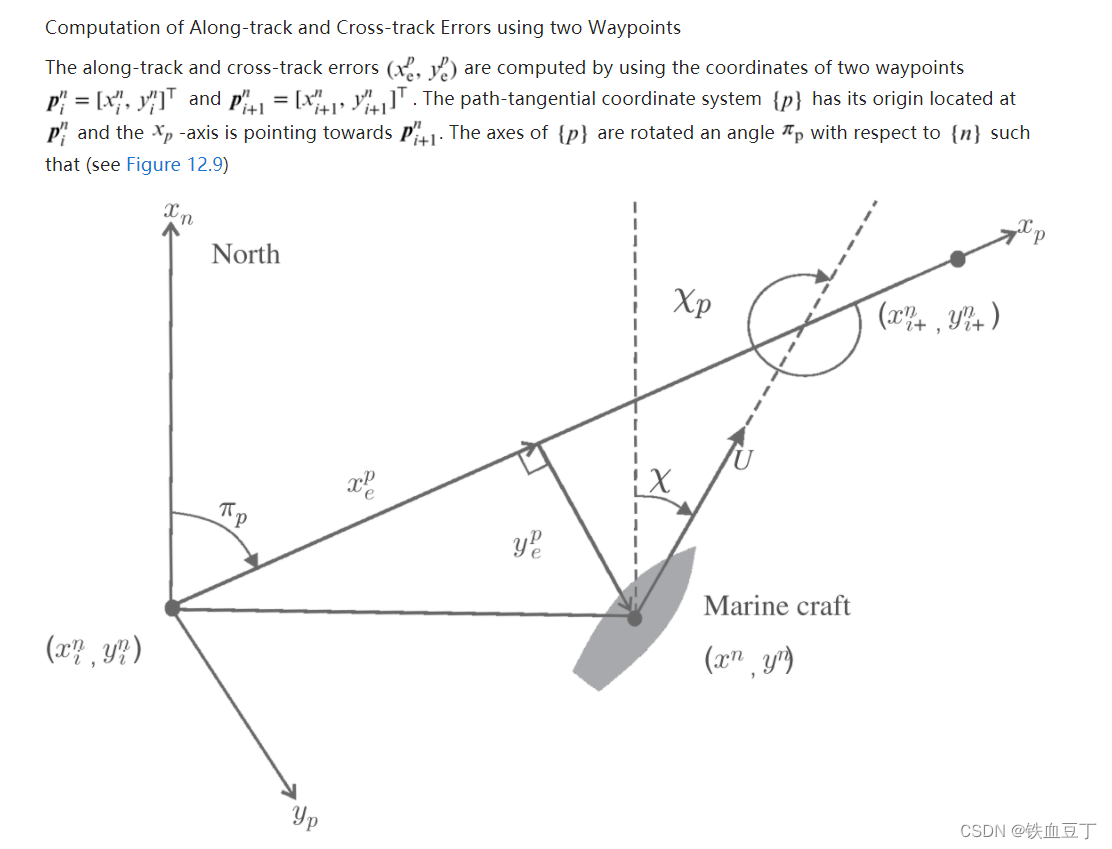
在这里插入图片描述

代码中，先对pi_p进行了求解，之后求解了xe和ye
在这里插入图片描述
评判是否到达下一个航路点的公式：
在这里插入图片描述
上述代码显示，当r比路径减去xe要大的时候，就该切换到下一个路径点了。

（2）制导率公式
在这里插入图片描述
进一步设计，为下面的非线性ILOS公式，如代码所示：
在这里插入图片描述

（3）ye导数
对ye求导，可得ye导数的公式：
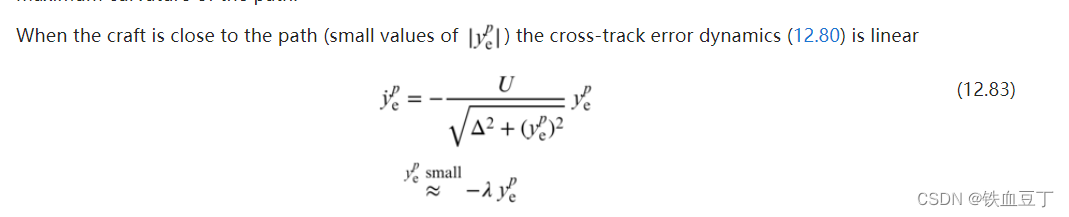
在这里插入图片描述
对期望航向角求导，就可以得到期望航向角速度的大小
在这里插入图片描述
（4）ye_int
在这里插入图片描述

总结

提示：这里对文章进行总结：

例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/799015.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

静态代理、jdk、cglib动态代理 搞不清？ 看这个文章就懂了

静态代理、jdk、cglib动态代理 搞不清？ 看这个文章就懂了

一、代理模式 代理模式是一种比较好的理解的设计模式。简单来说就是 &#xff1a; 我们使用代理对象来增强目标对象(target obiect)&#xff0c;这样就可以在不修改原目标对象的前提下&#xff0c;提供额外的功能操作&#xff0c;扩展目标对象的功能。将核心业务代码和非核心…
阅读更多...
linux下i2c调试神器i2c-tools安装及使用

linux下i2c调试神器i2c-tools安装及使用

i2c-tools介绍 在嵌入式linux开发中&#xff0c;有时候需要确认i2c硬件是否正常连接&#xff0c;设备是否正常工作&#xff0c;设备的地址是多少等等&#xff0c;这里我们就需要使用一个用于测试I2C总线的工具——i2c-tools。 i2c-tools是一个专门调试i2c的开源工具&#xff…
阅读更多...
Linux查看内存的几种方法

Linux查看内存的几种方法

PS的拼接方法 ps aux|head -1;ps aux|grep -v PID|sort -rn -k 4|head 进程的 status 比如说你要查看的进程pid是33123 cat /proc/33123/status VmRSS: 表示占用的物理内存 top PID&#xff1a;进程的ID USER&#xff1a;进程所有者 PR&#xff1a;进程的优先级别&#x…
阅读更多...
503、415、403、404报错

503、415、403、404报错

1、503 报错 Service Unvailable 解决&#xff1a;如果你用的是网关gateway&#xff0c;观察下你的项目是否导入了nacos依赖。 2、415 报错 Unsupported Media Type post传对象的时候&#xff0c;这样就会报错 解决&#xff1a;axios传对象的时候&#xff0c;用这种就可以了。…
阅读更多...
阿里内部都在疯传！企业级 Spring Boot 项目开发实战教程，先肝为敬

阿里内部都在疯传！企业级 Spring Boot 项目开发实战教程，先肝为敬

前言 本书结合大量的实际开发经验&#xff0c;由浅入深地讲解 Spring Boot 的技术原理和企业级应用开发涉及的的技术及其完整流程。无论是对 Java 企业级开发人员&#xff0c;还是 对其他相关技术爱好者&#xff0c;本书都极具参考价值。 本书特点 理论知识结合实践代码&#…
阅读更多...
专项练习-04编程语言-03JAVA-05

专项练习-04编程语言-03JAVA-05

1. 设有下面两个类的定义&#xff1a; class Person {} class Student extends Person { public int id; //学号 public int score; //总分 public String name; // 姓名 public int getScore(){return score;} } 类Person和类Student的关系是&#xff08;&#x…
阅读更多...
vue2中开发时通过template中的div等标签自动输出对应的less形式带层级的class,只显示带class的

vue2中开发时通过template中的div等标签自动输出对应的less形式带层级的class,只显示带class的

1.写完静态不是要写less吗&#xff0c;自动生成一下实现 this.getLevelClass(domId); domId是自定义的class名称&#xff0c;跟根据自己的需要设置 //vue2中开发时通过template中的div等标签自动输出对应的less形式带层级的class,只显示带class的getLevelClass(name) {let dom…
阅读更多...
Python基础语法第七章之文件

Python基础语法第七章之文件

目录 一、文件 1.1文件是什么 1.2文件路径 1.3文件操作 1.3.1 打开文件 1.3.2关闭文件 1.3.3写文件 1.3.4读文件 二、使用上下文管理器 2.1上下文管理器 一、文件 1.1文件是什么 变量是把数据保存到内存中. 如果程序重启/主机重启, 内存中的数据就会丢失. 要想能让…
阅读更多...
Excel 两列数据中相同的数据进行同行显示

Excel 两列数据中相同的数据进行同行显示

一、要求 假设您有两个列&#xff0c;分别是A列和B列&#xff0c;需要在C列中找出A列对应的B列的值。 二、方案 方法1&#xff1a;寻常思路 凸显重复项对A列单独进行筛选–按颜色进行排序&#xff0c;然后升序对B列重复上述操作即可 方法2&#xff1a;两个公式 VLOOKUP 纵向查找…
阅读更多...
【分享帖】LCD的MCU接口和SPI接口详解

【分享帖】LCD的MCU接口和SPI接口详解

LCD&#xff08;Liquid Crystal Display&#xff09;液晶屏&#xff0c;作为电子产品的重要组成部分&#xff0c;是终端用户与电子产品交互的重要载体。现在市场上的LCD&#xff0c;按照尺寸、功能、接口、用途等分为很多种&#xff0c;本文主要介绍如下两种LCD物理接口&#x…
阅读更多...
tinymce插件tinymce-powerpaste-plugin——将word中内容（文字图片等）直接粘贴至tinymce编辑器中

tinymce插件tinymce-powerpaste-plugin——将word中内容（文字图片等）直接粘贴至tinymce编辑器中

TinyMCE是一款易用、且功能强大的所见即所得的富文本编辑器。同类程序有&#xff1a;UEditor、Kindeditor、Simditor、CKEditor、wangEditor、Suneditor、froala等等。 TinyMCE的优势&#xff1a; 开源可商用&#xff0c;基于LGPL2.1 插件丰富&#xff0c;自带插件基本涵盖日常…
阅读更多...
Cesium态势标绘专题-直线箭头（标绘+编辑）

Cesium态势标绘专题-直线箭头（标绘+编辑）

标绘专题介绍：态势标绘专题介绍_总要学点什么的博客-CSDN博客 入口文件：Cesium态势标绘专题-入口_总要学点什么的博客-CSDN博客 辅助文件：Cesium态势标绘专题-辅助文件_总要学点什么的博客-CSDN博客 本专题没有废话，只有代码，代码中涉及到的引入文件方法，从上面三个链…
阅读更多...
网络安全大厂面试题

网络安全大厂面试题

自我介绍 有没有挖过src&#xff1f; 平时web渗透怎么学的&#xff0c;有实战吗&#xff1f;有过成功发现漏洞的经历吗&#xff1f; 做web渗透时接触过哪些工具 xxe漏洞是什么&#xff1f;ssrf是什么&#xff1f; 打ctf的时候负责什么方向的题 为什么要搞信息安全&#xff0c;对…
阅读更多...
照片加水印软件帮你搞定版权保护

照片加水印软件帮你搞定版权保护

嘿&#xff0c;亲爱的摄影爱好者&#xff01;是时候为你的照片保驾护航了&#xff01;想象一下&#xff0c;你在拍摄完一张美轮美奂的照片后&#xff0c;你为它加上个性化的水印&#xff0c;让每一个观者都知道这份艺术的创作者是你&#xff01;是不是觉得有点激动呢&#xff1…
阅读更多...
幻方问题（Magic Squares）

幻方问题（Magic Squares）

目录 基本介绍 丢勒-幻方 高阶幻方矩阵 习题 1. 幻方检测 2. durerperm 3. 颜色分配表 4. 幻方矩阵的逆矩阵 5. 幻方矩阵的秩 基本介绍 nn幻方是含有1到n^2的整数数组&#xff0c;排列后是的每一行、每一列、正反两条主对角线上数字的和都是相同的。对于每个n>2都有…
阅读更多...
Java类的默认构造函数

Java类的默认构造函数

什么情况下存在默认构造函数 说明 如果一个Java类没有显式包含构造函数的声明&#xff0c;那么隐含着有一个默认构造函数。 示例 定义一个类B&#xff0c;没有显式声明构造函数&#xff0c;所以存在一个默认构造函数&#xff1a; package com.thb;public class B {public …
阅读更多...
你说你会Java手动锁，但你会这道题吗？？？

你说你会Java手动锁，但你会这道题吗？？？

按照这个格式输出你会吗&#xff1f;&#xff1f;&#xff1f; 你说你不会&#xff0c;接下来认真看认真学了。 1.首先引入原子类。AtomicInteger num new AtomicInteger(0); 什么是原子类&#xff1f; 就是可以保证线程安全的原子操作的数据类型。 有什么作用&#xff1f;…
阅读更多...
Selenium结合Unittest

Selenium结合Unittest

1、Unittest&#xff1a;单元测试框架 ——对软件中的最小可测单元进行检查和验证 作用&#xff1a; 提供用例组织及执行提供丰富的断言方法&#xff08;判断实际结果与预期结果是否一致&#xff09;提供丰富的日志及测试结果 2、Unittest核心要素 TestCase&#xff08;测…
阅读更多...
易混淆-for循环中的break与return

易混淆-for循环中的break与return

1、for循环中的return不仅会跳出循环&#xff0c;还还会跳出当前函数。 2、for循环中的break只会跳出循环&#xff0c;结束for循环。 例&#xff1a;
阅读更多...
Git的远程操作与多人协作

Git的远程操作与多人协作

"爱在地图上剥落&#xff0c;我离孤单几公里~" 我们目前所说、所学的内容&#xff08;工作区、暂存区、版本库&#xff09;都只是存在于本地上&#xff0c;也就是说你的一台机器上只有这么一个你维护的版本库。可是Git是一个分布式版本控制系统&#xff0c;这又是什…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023