请同学们自行搜索或者想象一个象棋的棋盘，
然后把整个棋盘放入第一象限，棋盘的最左下角是(0,0)位置
那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域
给你三个 参数 x，y，k
返回“马”从(0,0)位置出发，必须走k步
最后落在(x,y)上的方法数有多少种?

一：暴力方法

	/**
     * 暴力方法
     */
    public static int jump(int a, int b, int k) {
        return process(a, b, k, 0, 0);
    }

    //返回落在a,b上并且走k步的方法数
    public static int process(int a, int b, int k, int x, int y) {
        if (k == 0) {
            return (x == a && y == b) ? 1 : 0;
        }

        //9行10列
        if (x < 0 || y < 0 || x > 9 || y > 8) {
            return 0;
        }

        int p1 = process(a, b, k - 1, x + 2, y + 1);
        int p2 = process(a, b, k - 1, x + 1, y + 2);
        int p3 = process(a, b, k - 1, x + 2, y - 1);
        int p4 = process(a, b, k - 1, x + 1, y - 2);
        int p5 = process(a, b, k - 1, x - 2, y + 1);
        int p6 = process(a, b, k - 1, x - 1, y + 2);
        int p7 = process(a, b, k - 1, x - 2, y - 1);
        int p8 = process(a, b, k - 1, x - 1, y - 2);

        return p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8;
    }

表格法

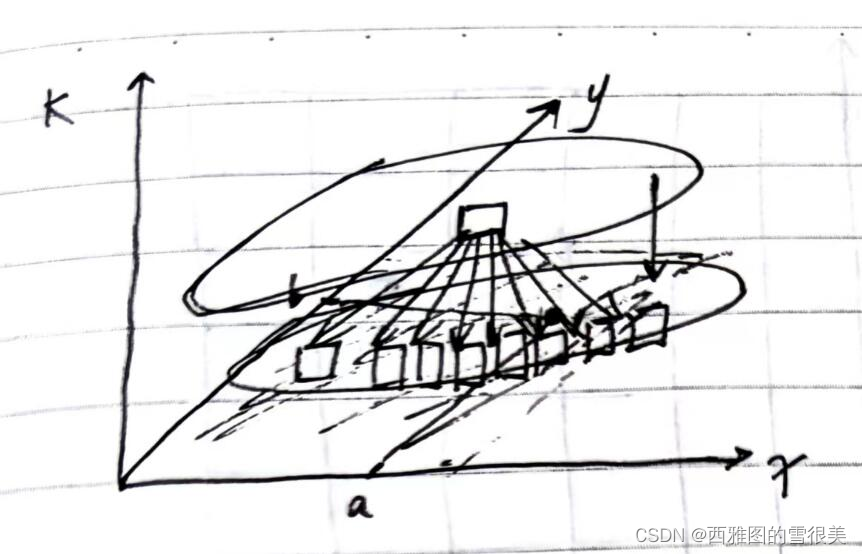
有三个变化的变量分别是：x，y，k 所以是一个三维的表格。

当层数是0的时候，只有（a,b,0）处是1，其他位置是0。

我还发现上一层是严格的依赖下一层的。上一层的每一个表格严格依赖下一层对应的八个表格（不越界的话）。

那填表的顺序就是由下往上一层一层的填表。

注意最后返回的是：dp[][][][] [ 0 ] [ 0 ] [ k ] 而不是 dp[][][][] [ a ] [ b ] [ k ] —> 表格法可以看成是递归的归过程。最终归的终点是最开始传入

进方法的起点位置。

本题可以想象一下：刚开始一定是(0,0,k) 之后向下层依赖，辐射到下一层的8个位置（不越界），之后下一层的8个位置继续向下层辐射8个位置，直到辐射到最底层，如果辐射到的最低层包含着(a,b,0)就算可以到达目标位置。

	/**
     * 迭代法
     */
    public static int dp(int a, int b, int k) {
        //这里需要考虑k以及k==0时的情况，所以取k的范围是k+1个
        int[][][] dp = new int[10][9][k + 1];
        //依赖关系是：上层依赖下层，最终返回最上层，所以从下向上构建
        dp[a][b][0] = 1;
        for (int plie = 1; plie <= k; plie++) {
            //这一层的每个数都依赖下一层。
            for (int x = 0; x < 10; x++) {
                for (int y = 0; y < 9; y++) {

                    int p1 = pick(dp, x + 2, y + 1, plie - 1);
                    int p2 = pick(dp, x + 1, y + 2, plie - 1);
                    int p3 = pick(dp, x + 2, y - 1, plie - 1);
                    int p4 = pick(dp, x + 1, y - 2, plie - 1);
                    int p5 = pick(dp, x - 2, y + 1, plie - 1);
                    int p6 = pick(dp, x - 1, y + 2, plie - 1);
                    int p7 = pick(dp, x - 2, y - 1, plie - 1);
                    int p8 = pick(dp, x - 1, y - 2, plie - 1);

                    dp[x][y][plie] = p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8;

                }
            }
        }

        return dp[0][0][k];//注意返回的是(0,0,k)这个坐标
    }

    public static int pick(int[][][] dp, int x, int y, int pile) {
        if (x < 0 || y < 0 || x > 9 || y > 8) {
            return 0;
        } else {
            return dp[x][y][pile];
        }
    }