把题中所给的式子进行展开，最终可以得到一个等比数列。运用等比数列求和公式即可。

相关知识点：欧拉降幂，逆元。

逆元的用处：因为求和公式需要去除分子，而大数除法去取模会丢失精度，所以可以采用求出分子在mod意义下的逆元，然后进行乘法运算即可。

欧拉降幂：因为文明需要求出等比数列的项数，而项数为2的1e18级别，对此我们在快速幂过程中必然会进行取模操作，而对于这种指数比较大的数，%c！=%c。所以需要进行欧拉降幂。 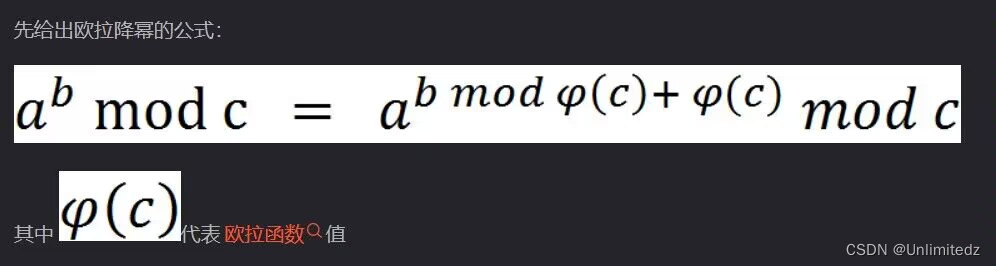而我们一个质数p的欧拉函数值即为 p-1.

#include<bits/stdc++.h>

using namespace std;
const int N=1e6+5;
typedef long long ll;
typedef pair<ll,ll> pll;
typedef array<int,3> p3;
ll mod=998244353;
const int maxv=4e6+5;

ll qmi(ll a,ll  b)
{
    ll res=1;
    while(b){
        if(b & 1) res=res*a%mod;
        b>>=1;
        a=(a%mod)*(a%mod) % mod;
    }
    return res%mod;
}

ll inv(ll x)
{
    return qmi(x,mod-2);
}



void solve()
{	

    ll n,x;
    cin>>n>>x;
    if(n==0){
        cout<<(1+x)%mod<<endl;
        return ;
    }
    if(x%mod==1) {
        ll ans=qmi(2,n+1);
        cout<<ans<<endl;
        return  ;
    }
    mod--;
    ll res=qmi(2,n+1);
    //cout<<res<<endl;
    //cout<<qmi(x,res)<<endl;
    mod++;
    ll f=(qmi(x,res)-1+mod)%mod;
    ll z=inv(x-1);
    //cout<<z<<endl;
    cout<<f*z%mod<<endl;




}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	t=1;
	//cin>>t;
	while(t--){
		//if(n==0) break;
		solve();
	}
	//system("pause");
	return 0;
}