123.买卖股票的最佳时机III

方法一：二维数组的讲解：

在这里插入图片描述

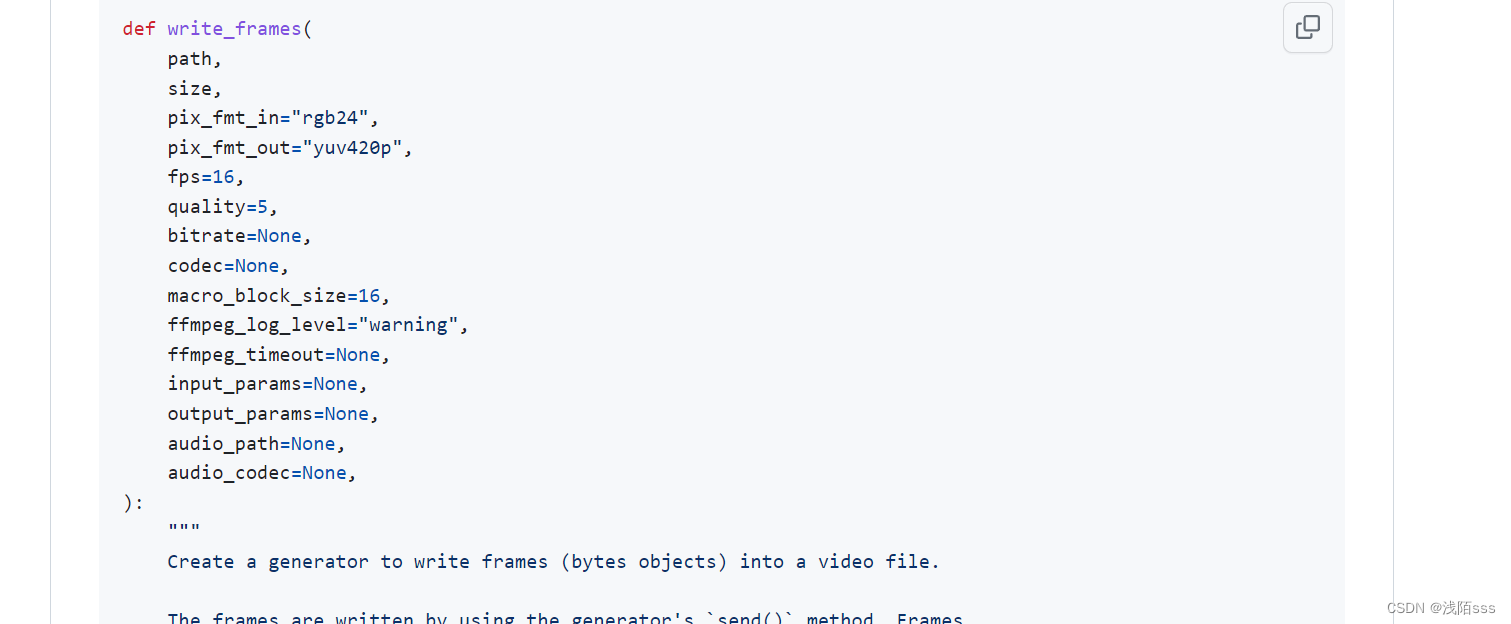
class Solution {
    public int maxProfit(int[] prices) {
     int day = prices.length;
     int[][] dp = new int[day][5];

     //初始化
     dp[0][1] = -prices[0]; //buy1的最大利润
     dp[0][3] = -prices[0]; //buy2的利润
     //开始遍历每一天
     for(int i=1;i<day;i++){
        dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] - prices[i]) ;    //buy1的最大利润: 1.昨天没有操作+今天买入的   2.保持昨天买入的原样
        dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] + prices[i]) ;   //sold1，最大的利润： 1.之前买入的 + 今天卖出  2.之前就卖了，保持原样
    
        dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]-prices[i]); // buy2的最大利润: 1.昨天卖出的+今天买入的   2.保持昨天买入的原样
        dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3] + prices[i]) ; // sold2，最大的利润： 1.之前买入的 + 今天卖出  2.之前就卖了，保持原样
     }
  return dp[day-1][4];
    }
}

空间优化，一维数组

class Solution {
    public int maxProfit(int[] prices) {
     int day = prices.length;
     int[] dp = new int[5];

     dp[1] = -prices[0];
     dp[3] = -prices[0];

     for(int i=1;i<day;i++){
        dp[1] = Math.max(dp[1],-prices[i]);
        dp[2] = Math.max(dp[2],dp[1]+prices[i]);
        dp[3] = Math.max(dp[3],dp[2] - prices[i]);
        dp[4] = Math.max(dp[4],dp[3]+prices[i]);
     }
     return dp[4];
    }
}

方法二：贪心算法

贪心算法

在只能进行一次股票交易，贪心算法，从前往后遍历，记录最底的价格以及最高的利润

class Solution {
    public int maxProfit(int[] prices) {
     int day = prices.length;
    int buy1 = Integer.MAX_VALUE; int buy2 = Integer.MAX_VALUE;
    int sold1 =0;  int sold2 =0;

     for(int i=0;i<day;i++){
       buy1 = Math.min(buy1,prices[i]); //找到最低的进货价格
       sold1 = Math.max(sold1, prices[i] - buy1); //找到第一次卖出的最高利润

       buy2 = Math.min(buy2, prices[i] - sold1 ); //找到第二次最低的进货价格（此时我已经用第一次卖出时候的利润了）
       sold2 = Math.max(sold2,  prices[i] - buy2); //sold2表示卖出两次之后的总利润
     }
     return sold2;
    }
}

188. 买卖股票的最佳时机 IV

方法一：在上一道题二维的基础上，变成三维
dp[天数] [交易次数][交易状态]
交易次数：0表示no-action， 1-k表示交易的次数
交易状态：0表示买入，buy ;1 表示卖出， sold

class Solution {
    public int maxProfit(int k, int[] prices) {
     int day = prices.length;
     int[][][] dp = new int[day][k+1][2];

     //1.初始化，对于每一次交易开始前，买入的利润为-，
     for(int i=1;i<=k;i++){
         dp[0][i][0] = -prices[0]; // dp[0][i][1] = 0;
     }

     //2.开始交易
     for(int i =1;i<day;i++){ // 天数
       for(int j =1;j<=k;j++){ // 轮次
       dp[i][j][0] = Math.max( dp[i-1][j][0],dp[i-1][j-1][1] - prices[i]);  // 买入时的利润，1.保持之前买入状态 2.卖出之前的-买入当天价格）
       dp[i][j][1] = Math.max(dp[i-1][j][1],dp[i-1][j][0]+ prices[i]);     //卖出的利润，1.保持 2.卖出之前的
       }
     }
     return dp[day-1][k][1];
    }
}

空间优化：一维数组

class Solution {
    public int maxProfit(int k, int[] prices) {
     int day = prices.length;
     int[] dp = new int[2*k+1];
    //0 表示no-action
    //1-2k,单数表示买入 ， 偶数表示卖出
    
    //1.初始化
    for(int i=1;i<=2*k;i+=2){ //1,3,5....
      dp[i] = -prices[0];
    }

    for(int i=1;i<day;i++){
      for(int j =1;j<=2*k; j+=2){
        dp[j] = Math.max(dp[j],dp[j-1]-prices[i]);
        dp[j+1] = Math.max(dp[j+1],dp[j]+prices[i]);
      }
    }
    return dp[2*k];
    }
}

方法二：贪心算法的改进

class Solution {
    public int maxProfit(int k, int[] prices) {
     //
     int[] buy = new int[k]; //每次交易买入的最低价格
     int[] sold = new int[k]; //每次交易之后，卖出的总利润

     Arrays.fill(buy,Integer.MAX_VALUE);
     for(int price :prices){ // i=0,表示第一次交易
       buy[0] = Math.min(buy[0],price);
       sold[0] = Math.max(sold[0],price-buy[0]);

      for(int i =1;i<k;i++){ 
         buy[i] = Math.min(buy[i],price-sold[i-1]);
         sold[i] = Math.max(sold[i],price-buy[i]);
      }
     }
return sold[k-1];
    }
}