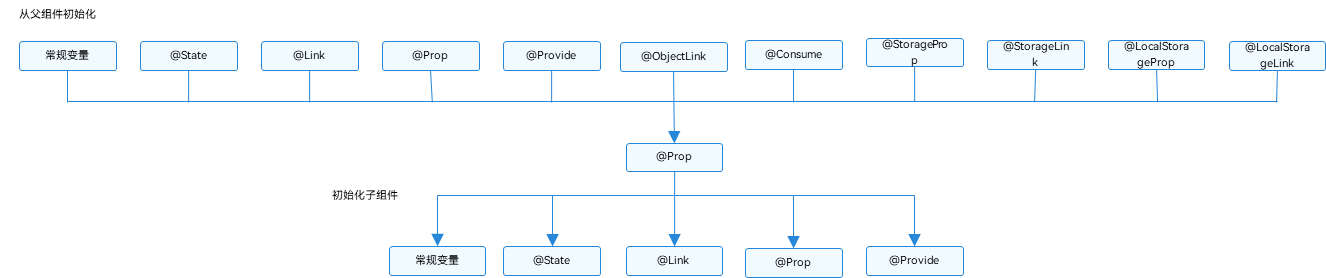
题目链接
点击打开链接
题目解法
首先做一个重要的转化：把
b
i
b_i
bi 单调上升变为
b
i
b_i
bi 单调不降
如何转化？将
a
i
−
i
a_i-i
ai−i 变成新的
a
i
a_i
ai，将
b
i
−
i
b_i-i
bi−i 变新的
b
i
b_i
bi，这样答案是不变的，且
b
i
b_i
bi 变成了单调不降
考虑对于两段相邻序列
a
1
,
.
.
.
,
a
n
a_1,...,a_n
a1,...,an 和
a
n
+
1
,
.
.
.
,
a
n
+
m
a_{n+1},...,a_{n+m}
an+1,...,an+m，最优的一组
b
b
b 分别为
b
1
,
.
.
.
,
b
n
(
b
1
=
b
2
=
.
.
.
=
b
n
)
b_1,...,b_n(b_1=b_2=...=b_n)
b1,...,bn(b1=b2=...=bn) 和
b
n
+
1
,
.
.
.
,
b
n
+
m
(
b
b
+
1
=
b
n
+
2
=
.
.
.
=
b
n
+
m
)
b_{n+1},...,b_{n+m}(b_{b+1}=b_{n+2}=...=b_{n+m})
bn+1,...,bn+m(bb+1=bn+2=...=bn+m)
考虑合并之后的
b
1
,
.
.
.
,
b
n
+
m
b_1,...,b_{n+m}
b1,...,bn+m
令
b
1
=
u
,
b
n
+
1
=
v
b_1=u,\;b_{n+1}=v
b1=u,bn+1=v
- u ≤ v u\le v u≤v， b i b_i bi 的值不用改变，直接合并即可
-
u
>
v
u>v
u>v
令合并后的答案为 c 1 , . . . , c n + m c_1,...,c_{n+m} c1,...,cn+m
考虑结论： c n ≤ u c_n\le u cn≤u
证明：如果有 c n > u c_n>u cn>u，那么把 c 1 , . . . , c n c_1,...,c_n c1,...,cn 替换成 u u u 也是一组合法的解，且答案不会变劣
同理可得 c n + 1 ≥ v c_{n+1}\ge v cn+1≥v
考虑最优解 c 1 , . . . , c n + m ( c n ≤ u , c n + 1 ≥ v ) c_1,...,c_{n+m}(c_n\le u,\;c_{n+1}\ge v) c1,...,cn+m(cn≤u,cn+1≥v)
把 c 1 , . . . , c n + m c_1,...,c_{n+m} c1,...,cn+m 替换为 a 1 , . . . , a n + m a_1,...,a_{n+m} a1,...,an+m 的中位数 k k k 答案不会更劣
证明：若 c 1 > k c_1>k c1>k 或 c n + m < k c_{n+m}<k cn+m<k，那么易知可以替换；若 c n < k c_n<k cn<k 且 c n + 1 > k c_{n+1}>k cn+1>k，根据 1 − n 1-n 1−n 中 ≥ u \ge u ≥u 的 a i a_i ai 一定不小于一半， n + 1 − m n+1-m n+1−m中 l e v le v lev 的 a i a_i ai 一定不小于一半可以证得
所以可以一个一个添加数，一段一段往前合并即可
考虑如何合并？用左偏树维护前一半的最大值
考虑合并如何合并两个左偏树？直接合并即可
直接合并左偏树维护中位数在没有限制的两个序列中是不对的
但这道题中是有特殊限制的
考虑新的中位数一定出现在橘色框内，且上面序列的橘色框是维护到了，但下面序列的橘色框内是没有维护到的，但因为只添加了一个数，且之前的中位数是大于上方序列的中位数的，所以下面序列的橘色框内没有数，所以直接合并恰好是可行的
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N(1000100);
struct Node{
int ed,rt,siz;
}stk[N];
int n,a[N],ans[N];
int lc[N],rc[N],dist[N],v[N];
inline int read(){
int FF=0,RR=1;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
return FF*RR;
}
int merge(int x,int y){
if(!x||!y) return x|y;
if(v[x]<v[y]) swap(x,y);
rc[x]=merge(rc[x],y);
if(dist[rc[x]]>dist[lc[x]]) swap(lc[x],rc[x]);
dist[x]=dist[rc[x]]+1;
return x;
}
int main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read(),a[i]-=i;
int top=0;
for(int i=1;i<=n;i++){
v[i]=a[i],dist[i]=1;
Node t={i,i,1};
while(top&&v[t.rt]<v[stk[top].rt]){
t.rt=merge(t.rt,stk[top].rt);
if((t.siz&1)&&(stk[top].siz&1)) t.rt=merge(lc[t.rt],rc[t.rt]);
t.siz+=stk[top].siz;
top--;
}
stk[++top]=t;
}
for(int i=1,j=1;i<=n;i++){
if(i>stk[j].ed) j++;
ans[i]=v[stk[j].rt];
}
LL tot=0;
for(int i=1;i<=n;i++) tot+=abs(ans[i]-a[i]);
printf("%lld\n",tot);
for(int i=1;i<=n;i++) printf("%d ",ans[i]+i);
return 0;
}
