进制和进制转换

news2024/11/25 7:42:30

什么是进制

进制的全称是进位计数制，是人为定义的带进位的计数方法，对于任何一种X进制，就表示每一位置上的数运算时都是逢 X进一位。十进制是逢十进一，十六进制是逢十六进一，二进制就是逢二进一，以此类推，X进制就是逢X进位。

常用的进制

二进制（数码：0,1）
八进制（数码：0,1,2,3,4,5,6,7）
十进制（数码：0,1,2,3,4,5,6,7,8,9,）
十六进制（数码：0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F）

进制的前缀、后缀

为了区分数字的进制，常常在数字的后面加上英文字母作为后缀或者在数字的前面加上前缀

进制	数码范围	前缀	后缀
二进制	0~1	0b(0B)	B
八进制	0~7	0	Q
十进制	0~9	无()	D
十六进制	0~9,A-F	0X	H

比如：11101B（二进制） 123Q（八进制） 567D（十进制） C7AH（十六进制）
也可以用加括号下标表示法：如（11101）2

进制转化

1.十进制

十进制共有10个数码{0，1，2，3，4，5，6，7，8，9}，它的特点是逢 10进1。

二进制转十进制：按权展开后相加，下面是几个示例

十进制转二进制：方法：整数部分除基(2)取余，倒序排列；小数部分乘基(2)取整，正序排列。

例题：将十进制数 28 转换为二进制数

例题：将十进制数 16.6875 转换为二进制数

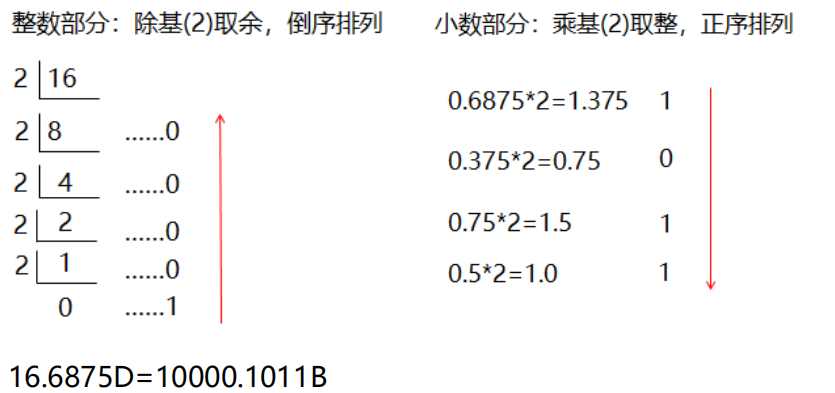
2.八进制

八进制共有8个数码{0，1，2，3，4，5，6，7}，它的特点是逢 8进1。

八进制转十进制： 按权展开后相加，下面是几个示例

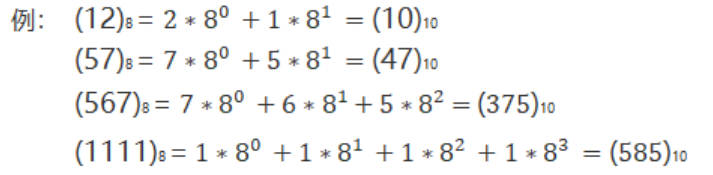
十进制转八进制方法： 整数部分除基(8)取余，倒序排列；小数部分乘基(8)取整，正序排列。

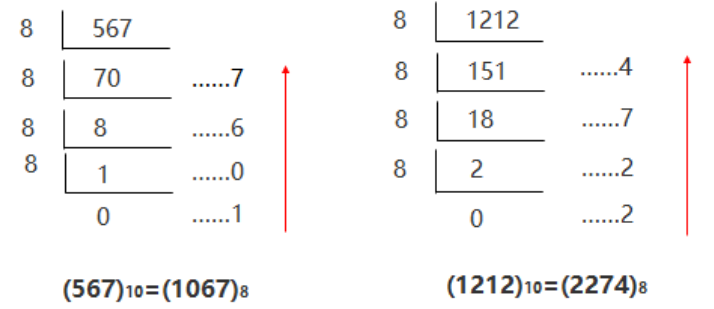
八进制与二进制转换方法： 三分法（想一想为什么可以用这种方法）
由于2^3=8,八进制与二进制有一种对应的关系，如下图：

八进制	0	1	2	3	4	5	6	7
二进制	000	001	010	011	100	101	110	111

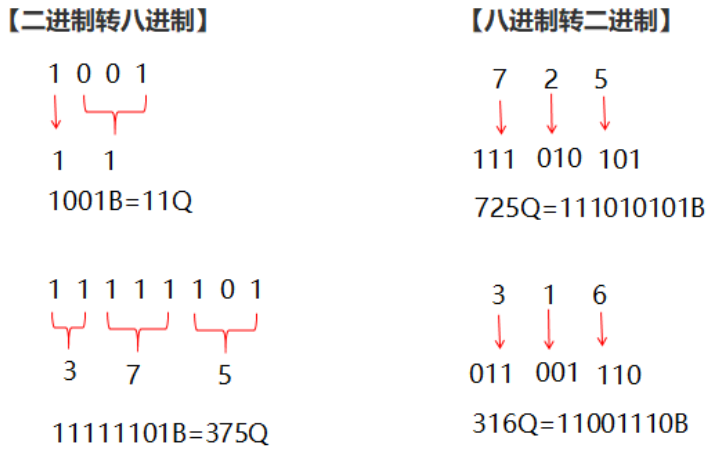
例题1： 请你编写一个程序，将八进制数转换成十进制数。

解题思路： 首先利用数位分离分离出每一位数字，然后i从1开始累乘，每次乘8即可。完整的代码如下，除此之外，你还能想到几种其它的代码吗？

#include<bits/stdc++.h>
using namespace std; 
int fun(int x)
{
    int i=1,sum=0;
    while(x!=0)
    {
        sum=sum+(x%10)*i;
        x=x/10;
        i=i*8;
    }
    return sum;
}
int main() 
{
    int x;
    cin>>x;
    cout<<fun(x)<<endl;
}

例题2： 请你编写一个程序，将十进制数转换成八进制数。

解题思路： 首先利用将x对8取余，每次模的结果放在一个数组里面，同时x每次更新为x/8，最后只要逆序输出数组里面的数字就可以了。完整的代码如下，除此之外，你还能想到几种其它的代码？

#include<bits/stdc++.h>
using namespace std; 
int main() 
{
    int n=0,x,a[100];
    cin>>x;
    while(x!=0)
    {
        n++;
        a[n]=x%8;
        x=x/8;
    }
    for(int i=n;i>=1;i--) 
        cout<<a[i];
    return 0;

}

3.十六进制

十六进制共有16个数码{0，1，2，3，4，5，6，7，8,9，A，B，C，D，E，F}，它的特点是逢 16进1。

十六进制转十进制： 按权展开后相加，下面是几个示例

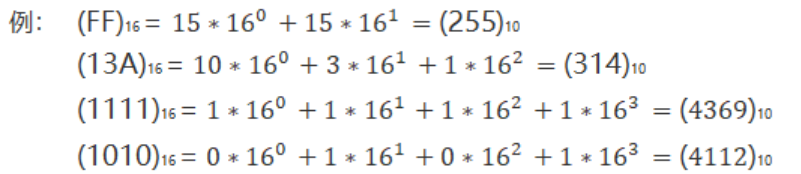
十六进制与二进制转换： 方法：四分法（想一想为什么可以用这种方法）

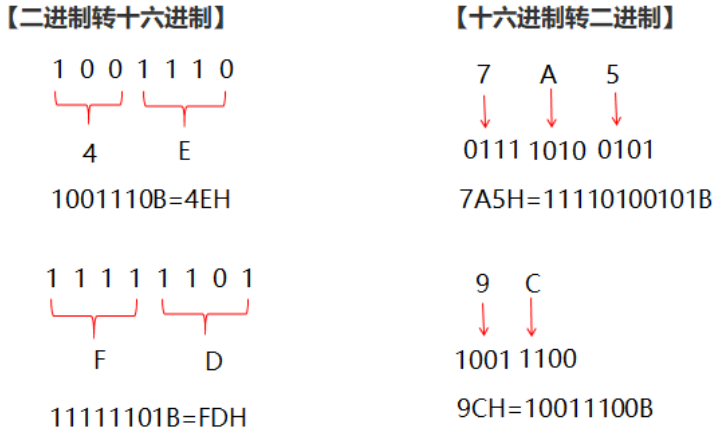
相信通过上面的介绍，同学们已经对什么是二进制、八进制、十进制以及十六进制已经了如指掌了吧。那么接下来再让我们如何利用C++进行进制之间的转换吧。

例题3：输入一个b进制的数字a，将其转换成对应的十进制数字(在int范围内)。

样例输入： 共一行，为两个数字，第一个为数字a，第二个为进制b；

样例输出： 为一个数字，表示对应的十进制数字

样例输入1：

101 2

样例输出1：

解题思路： 将数字存在字符串里，从后往前遍历整个字符串，因为可能是16进制会有ABCDEF，因此需要对a[i]进行判断，如果是a[i]>='A'则t=a[i]-65+10，否则t=a[i]-48。然后将t乘上b的k次方就可以了，k从0开始每次加1。

#include<bits/stdc++.h>
using namespace std;
int main( )
{
    string a;        //将数字存在字符串里
    int b,i,s=0,k=1,t;
    cin>>a>>b;       //输入这个数和进制
    for(i=a.size()-1;i>=0;i--)  //从后往前
    {//选择运算符
        t=(a[i]>='A'?a[i]-65+10:a[i]-48); //因为可能是16进制会有ABCDEF，因此需要对a[i]进行判断，如果是a[i]>='A'则t=a[i]-65+10，否则t=a[i]-48。
         s=s+t*k;
         k=k*b;
    }
    cout<<s; 
}

例题4： 输入一个十进制的数字a，将其转换成对应的b进制数字(在int范围内)。

样例输入： 共一行，为两个数字，第一个为数字a，第二个为进制b；

样例输出： 为一个数字，表示对应的十进制数字

样例输入1：

101 8

样例输出1：

解题思路： 还是利用字符串帮助实现。首先求a%b的余数，将余数加48转换成字符型，考虑到16进制，如果大于’9’要转换成字母ABCDEF，然后利用字符串的拼接和翻转实现将一个十进制的数字a，转换成对应的b进制数字。

#include<bits/stdc++.h>
using namespace std;
int main( )
{
    int a,b;
    string c;  //c是字符串
    cin>>a>>b;
    if(a==0){
        cout << 0;
        return 0;
    }
    while(a!=0)
    {
        char t=a%b+48;  //t是字符型，把数字存进字符串里加48
        if(t>'9') //这里是字符’9’，考虑16进制
        {
            t=64+t-'9';  //如果超过9，转换成字母ABCDEF
        } 
        c=c+t; //字符串拼接
        a=a/b; //更新a的值
    }
    reverse(c.begin(),c.end()); //逆序输出即可
    cout<<c;
}

例题5： 输入一个b进制的数字a，将其转换成对应的c进制数字(十进制数字在int范围内)。

样例输入：共一行，为三个数字，第一个为数字a，第二个为当前进制b，第三个为待转化进制c

样例输出：为一个数字，表示对应的c进制数字

样例输入1：

101 10 8

样例输出1：

解题思路： 先转成十进制，再从十进制转为其他进制。本题是进制转换章节最重要的一题，因为只要会了这一题，可以解决任何进制之间的转换问题，因此希望同学一定要熟练掌握。

#include<bits/stdc++.h>
using namespace std;
int _zhuan10(string a,int b)
{
    int s=0,k=1,t,len=a.size();
    for(int i=len-1;i>=0;i--)
    {
        t=(a[i]>='A'?a[i]-65+10:a[i]-48);
        s=s+t*k;
        k=k*b;
    }
    return s;
}
string _10zhuan(int a,int b)
{
    string c;
    while(a!=0)
    {
        char t=a%b+48;
        if(t>'9')
        {
            t=64+t-'9'; 
        } 
        c=c+t;
        a=a/b;
    }
    reverse(c.begin(),c.end());
    return c;   
} 
int main()
{
    string a;
    int b,c;
    cin>>a>>b>>c;
    if(a=="0")
    {
        cout<<0;
        return 0;
    }
    int t=_zhuan10(a,b);
    cout<<_10zhuan(t,c); 
}