本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], ..., nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
示例 1:
输入:nums = [1,-2,3,-2]
输出:3
解释:从子数组 [3] 得到最大和 3
示例 2:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
示例 3:
输入:nums = [3,-2,2,-3]
输出:3
解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
提示:
n == nums.length1 <= n <= 3 * 10^4-3 * 10^4 <= nums[i] <= 3 * 10^4
解法 动态规划
首先要掌握好53题,最大子数组和的动态规划解法.
这题一共有两种情况(也就是比53题多了一种「最大非空子数组和是首尾连接」的情况) 下面的这个子数组指最大和的子数组。
- 第一种情况:这个子数组不是环状的,就是说首尾不相连。
- 第二种情况:这个子数组一部分在首部,一部分在尾部,我们可以将这第二种情况转换成第一种情况。如下图:
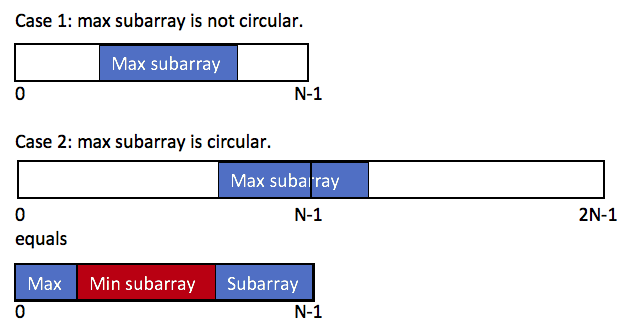
所以这最大的环形子数组和 = max ( 最大子数组和 , 数组总和 − 最小子数组和 ) \max(最大子数组和,\ 数组总和-最小子数组和) max(最大子数组和, 数组总和−最小子数组和) 。
证明:第二种情况(最大子数组是环形的) max ( 前缀数组 + 后缀数组 ) = max ( 数组总和 − s u b a r r a y ) = 数组总和 + max ( − s u b a r r a y ) \max(前缀数组+后缀数组) = \max(数组总和 - subarray)\\ = 数组总和 + \max(-subarray) max(前缀数组+后缀数组)=max(数组总和−subarray)=数组总和+max(−subarray) 数组总和是不变的,直接提出来 = 数组总和 − min ( s u b a r r y ) = 数组总和 - \min(subarry) =数组总和−min(subarry) 。 s u b a r r a y subarray subarray 指的是前缀数组和后缀数组中间的数组。再把负号提出来, max \max max 变成 m i n min min 。
极端情况:如果说这数组的所有数都是负数,由于要返回非空子数组的和,那么上面的公式还需要变一下,因为这时,对于上面的情况①, s u m sum sum 会等于数组中的最大值,而情况② s u m = 0 sum=0 sum=0(最小的子数组就是本数组, t o t a l − t o t a l = 0 total-total=0 total−total=0 )。所以多加一个Case,判断最大子数组和是否小于0,小于0,直接返回该 m a x S u b A r r a y maxSubArray maxSubArray 。
令 t o t a l total total 为数组的总和, m a x S u m maxSum maxSum 为最大子数组和, m i n S u m minSum minSum 为最小子数组和, c u r M a x curMax curMax 为包含当前元素的最大子数组和, c u r M i n curMin curMin 为包含当前元素的最小子数组和。
class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
int total = 0, maxSum = nums[0], curMax = 0, minSum = nums[0], curMin = 0;
for (int num : nums) {
curMax = max(curMax + num, num);
maxSum = max(maxSum, curMax);
curMin = min(curMin + num, num);
minSum = min(minSum, curMin);
total += num;
}
return maxSum > 0 ? max(maxSum, total - minSum) : maxSum;
}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)