卡尔曼滤波器的过程

卡尔曼滤波器的过程分为：
- 状态方程：
  $x_k=Ax_{k-1}+Bu_{k-1}+\omega_{k-1} \\ z_k=Hx_k+\nu_k \\ 这样就得到了状态方程和观测方程的表达式 \\ 其中 x_k 是状态向量，A是转移矩阵，B是输入转换为状态的矩阵，u_k是系统输入，\omega_{k}是系统噪声 \\ z_k是测量值（不一定为标量），H是状态向量到测量值的转换矩阵，\nu_k是测量噪声$
- 预测：
  1. 计算先验： $\hat{x}_k^-=A\hat{x}_{k-1}+Bu_{k-1}$
  2. 计算先验误差协方差矩阵： $P_k^-=AP_{k-1}A^T+Q$
- 校正：
  3. 计算卡尔曼增益： $K_k=P_k^-H^T(HP_k^-H^T+R)^{-1}$
  4. 计算后验估计： $\hat{x}_k=\hat{x}_k^- + K_k(z_k-H\hat{x}_k^-)$
  5. 更新先验误差协方差矩阵： $P_k=(I-K_kH)P_k^-$

加深理解

字数超出，参考【【卡尔曼滤波器】1_递归算法_Recursive Processing】 https://www.bilibili.com/video/BV1ez4y1X7eR/?share_source=copy_web&vd_source=f888a64d6daca22a15191528d732f02a

卡尔曼滤波器详细推导

字数超出，参考【【卡尔曼滤波器】1_递归算法_Recursive Processing】 https://www.bilibili.com/video/BV1ez4y1X7eR/?share_source=copy_web&vd_source=f888a64d6daca22a15191528d732f02a

卡尔曼滤波器的应用

python中使用

在 filterpy 这个包中已经实现了卡尔曼滤波器，其一般用法为：

# 首先从 filterpy 中导入卡尔曼滤波器
from filterpy.kalman import KalmanFilter

# 创建实例
# dim_x 是状态向量的维度，dim_z 是测量向量的维度
kf = KalmanFilter(dim_x=*, dim_z=*)

# 设置初始状态，即 \hat{x}_0，维度为 (dim_x, 1)
kf.x = np.array([[*], [*], ...])

# 设置状态转移矩阵，即公式中的 A 矩阵，维度为 (dim_x, dim_x)
kf.F = np.array()

# 设置状态向量到测量值的转换矩阵，即前面公式中的 H 矩阵，维度为 (dim_z, dim_x)
kf.H = np.array()

# 设置过程噪声的协方差矩阵 Q，即公式中 \omega 的协方差矩阵，维度为 (dim_x, dim_x)
# 该值往往不确定，需要根据场景自己设置，寻找一个能得到良好结果的值
kf.Q = np.array()

# 设置测量噪声的协方差矩阵 R，即公式中 \nu 的协方差矩阵，维度为 (dim_z, dim_z)
# 该值往往也不确定，需要自己确定
kf.R = np.array()

# 设置先验误差的协方差矩阵 P，即公式中的 P，维度为 (dim_x, dim_x)
# 由于该值后续会迭代更新，因此初值不影响，但如果给定的初始值 x 不可信，我们会将P中对应位置设置一个较大的数，来表示第一次先验值的不可信，默认是一个单位矩阵
kf.P = np.array()

# 创建一个列表，记录所有过程中的估计值
x_estimate = []

# 开始迭代预测
for i in range(数据长度):
    kf.predict() # 先执行第一次预测
    kf.update(z_i) # 然后根据当前测量值进行更新，测量值z的维度为 (dim_z, 1)
    x_estimate.append(kf.x) # 保存估计值

我们来用它模拟一个二维平面上的物体轨迹跟踪

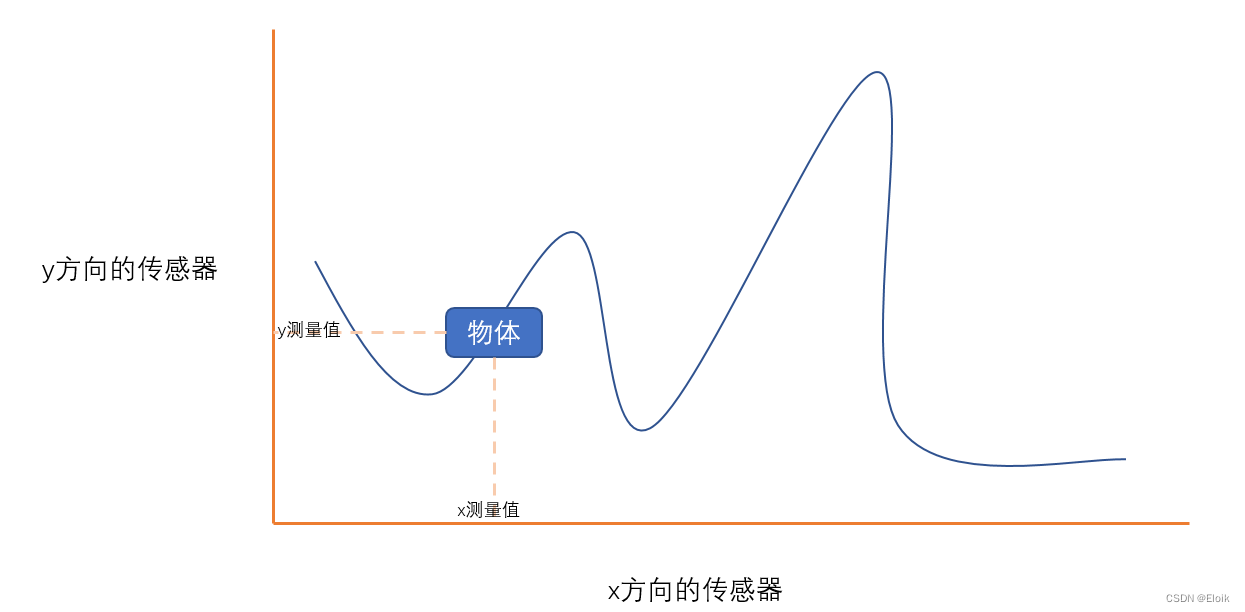
在这里插入图片描述

假如在一个平面上有一个运动的物体，它的轨迹如上图所示
$\\ 因此我们的测量值向量就是 z=\begin{pmatrix}x\\y\end{pmatrix} \\ 而对于物体来说，它本身的状态包括x和y方向的位置以及x和y方向的速度 \\ 因此我们可以定义状态向量 x=\begin{pmatrix}x\\y\\v_x\\v_y\end{pmatrix}，此时我们可以计算出状态向量到测量向量的转移矩阵 H \\ 显然有 z=\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1&0&0&0\\0&1&0&0\end{pmatrix}\begin{pmatrix}x\\y\\v_x\\v_y\end{pmatrix}，因此 H=\begin{pmatrix}1&0&0&0\\0&1&0&0\end{pmatrix} \\ 假如上一个状态向量 x_{k-1} = \begin{pmatrix}x_{k-1}\\y_{k-1}\\v_{x_{k-1}}\\v_{y_{k-1}}\end{pmatrix} \\ 假如速度不变，那么显然有 \begin{cases} x_k=x_{k-1}+v_{x_{k-1}}\Delta t \\ y_k=y_{k-1}+v_{y_{k-1}}\Delta t \\ v_{x_k} = v_{x_{k-1}} \\ v_{y_k} = v_{y_{k-1}} \end{cases} \\ 即 x_k = \begin{pmatrix} 1&0& \Delta t &0 \\ 0&1& 0 &\Delta t \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} x_{k-1} \\ 故状态转移矩阵 A=\begin{pmatrix} 1&0& \Delta t &0 \\ 0&1& 0 &\Delta t \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix}，过程输入一项为 0$
上面我们已经得到了 $A$ 和 $H$ 的值，还有 $Q$ ， $R$ ， $P$ 未知，因为我们使用正态分布对真实值添加噪声，因此正态分布的方差就是 $R$ 矩阵对角线的值，则 $R$ 矩阵也为已知， $P$ 矩阵会随迭代过程更新，初始值并不重要，我们使用默认的单位矩阵，而对于 $R$ 的设置，详见下面的代码

import numpy as np
from scipy import stats
from filterpy.kalman import KalmanFilter
import matplotlib.pyplot as plt

# 采样1000次
size = 1000

# 定义真实的轨迹值，其中 x 轴匀速变化，y轴按函数变化
x_true = np.linspace(0, 100, size)
y_true = (np.sin(np.pi * np.sqrt(x_true)) + np.log(x_true + 1)) * (np.sqrt(x_true) - 7)

# 定义每一步的观测值，在真实值上添加测量噪声作为测量值
sigma_x2 = 0.5  # x方向上测量噪声的方差
sigma_y2 = 0.5  # y方向上测量噪声的方差
x_mea = x_true + stats.norm.rvs(loc=0, scale=sigma_x2, size=size)
y_mea = y_true + stats.norm.rvs(loc=0, scale=sigma_y2, size=size)

# 创建实例
kf = KalmanFilter(dim_x=4, dim_z=2)

# 设置采样时间间隔，与前面 x_true=np.linspace 的采样间隔相等，即每隔0.1个单位采样一次
t = 100 / size
# 设置初始状态为 x方向位置0，y方向位置0，x方向速度1，y方向速度1
kf.x = np.array([[0], [0], [1], [1]])
# 设置状态转移矩阵
kf.F = np.array([[1, 0, t, 0], [0, 1, 0, t], [0, 0, 1, 0], [0, 0, 0, 1]])
# 设置状态向量到测量值的转换矩阵
kf.H = np.array([[1, 0, 0, 0], [0, 1, 0, 0]])
# 设置过程噪声的协方差矩阵 Q，该值参考了 《Bayesian Filtering and Smoothing》，Simo Sarkka著
# https://zhuanlan.zhihu.com/p/148046908
qc1, qc2 = 1, 1
kf.Q = np.array([[qc1 * t ** 3 / 3, 0, qc1 * t ** 2 / 2, 0],
                 [0, qc2 * t ** 3 / 3, 0, qc2 * t ** 2 / 2],
                 [qc1 * t ** 2 / 2, 0, qc1 * t, 0],
                 [0, qc2 * t ** 2 / 2, 0, qc2 * t]])
# 设置测量噪声的协方差矩阵 R，使用了前面人为制造噪声时的方差
kf.R = np.array([[sigma_x2, 0], [0, sigma_y2]])
# 设置先验误差的协方差矩阵 P，按默认的单位矩阵进行初始化
kf.P = np.eye(4)

# 记录估计过程
x_pred = []
y_pred = []
for i in range(size):
    kf.predict()
    kf.update(np.array([[x_mea[i]], [y_mea[i]]]))
    # 将预测结果保存
    x_pred.append(kf.x[0])
    y_pred.append(kf.x[1])

# 绘制结果
plt.plot(x_true, y_true, color='red', label="true value")
plt.plot(x_mea, y_mea, alpha=0.2, color='green', label='measurement value')
plt.plot(x_pred, y_pred, color='blue', label="estimate value")
plt.legend()
plt.show()

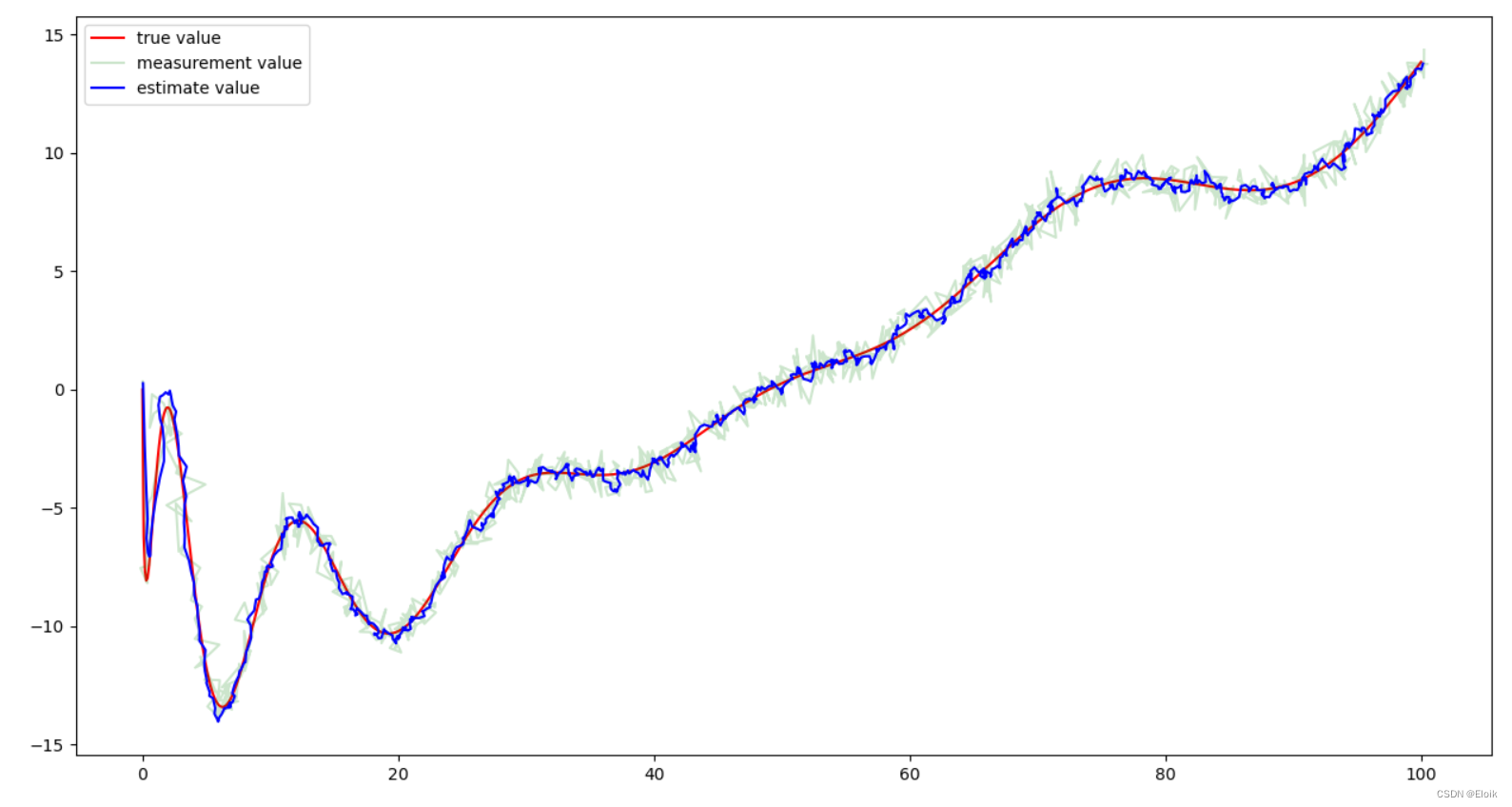
在这里插入图片描述

从图中可以看出，蓝色的估计值相较于绿色的观测值来说，更加靠近红色的真实值，这说明卡尔曼滤波器在本例中确实减小了测量噪声的影响。

单目标追踪

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JwaPBrnz-1670688580090)(./assets/1.gif)]

现在我们将目光放在单目标的追踪上面，以上面的只因为例，我们想要对其脸部进行追踪，如果使用 RetinaFace 模型对每一帧进行预测，将会在每一帧得到一个预测框，下面我们将预测框绘制在视频中

可以看出预测框精度虽好，但放在视频中会出现不平滑的现象，为了将框变得更加平滑，我们可以使用卡尔曼滤波来完成这项任务
$对于预测框来说，它形如\space (x_{min}, y_{min}, x_{max}, y_{max})，代表了框的左上角坐标和右下角坐标 \\ 在追踪任务中，我们一般将其变成另一种表达形式：(cx, cy, s, r) \\ 其中\space cx、cy \space表示框的中心坐标，s \space表示框的面积，r \space表示框的宽高比 \\ 在此基础上，对中心坐标和框的面积增加变化速度，那么框的状态向量表示为\space x=\begin{pmatrix} cx \\cy \\s \\r \\cx_v \\cy_v \\s_v\end{pmatrix} \\ 此时我们可以计算出状态向量到测量向量的转移矩阵\space H \\ 显然有\space z=\begin{pmatrix}cx\\cy\\s\\r \end{pmatrix} =\begin{pmatrix} 1&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0 \\ 0&0&1&0&0&0&0 \\ 0&0&0&1&0&0&0 \end{pmatrix} \begin{pmatrix} cx \\cy \\s \\r \\cx_v \\cy_v \\s_v\end{pmatrix}，因此\space H=\begin{pmatrix} 1&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0 \\ 0&0&1&0&0&0&0 \\ 0&0&0&1&0&0&0 \end{pmatrix} \\ 假设上一个状态向量 \space x_{k-1} = \begin{pmatrix} cx_{k-1} \\cy_{k-1} \\s_{k-1}\\r_{k-1}\\cx_{v_{k-1}}\\cy_{v_{k-1}} \\s_{v_{k-1}}\end{pmatrix}，假如速度不变，显然有 \begin{cases} cx_k = cx_{k-1} + cx_{v_{k-1}} \Delta t \\ cy_k = cy_{k-1} + cy_{v_{k-1}} \Delta t \\ s_k = s_{k-1} + s_{v_{k-1}} \Delta t \\ r_k = r_{k-1} \\ cx_{v_k} = cx_{v_{k-1}} \\ cy_{v_k} = cy_{v_{k-1}} \\ s_{v_k} = s_{v_{k-1}} \end{cases} \\ 即\space x_k = \begin{pmatrix} 1&0&0&0&0&\Delta t&0&0 \\ 0&1&0&0&0&0&\Delta t&0 \\ 0&0&1&0&0&0&0&\Delta t \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&1 \end{pmatrix} x_{k-1}，在本例中，\Delta t \space是一帧，因此这里\space \Delta t = 1 \\ 故状态转移矩阵\space A = \begin{pmatrix} 1&0&0&0&0&1&0&0 \\ 0&1&0&0&0&0&1&0 \\ 0&0&1&0&0&0&0&1 \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&1 \end{pmatrix}$
关于噪声协方差矩阵 $R, P, Q$ 的设置，对于追踪任务来说，往往使用经验数值，详见下方的代码

import numpy as np
from filterpy.kalman import KalmanFilter
import cv2


def load_pred_boxes(path):
    """
    加载 RetinaFace 模型预测的每一帧图像中人脸方框的坐标，`#`表示该帧没有检测到人脸

    :param path: 文件路径，该文件通过 RetinaFace 模型预测生成
    :return: 预测框列表
    """
    with open(path, 'r') as f:
        pred_boxes = f.readlines()
        pred_boxes = [i.strip() for i in pred_boxes]
        pred_boxes = [
            None if box == '#'
            else [float(i) for i in box.split(',')]
            for box in pred_boxes
        ]
    return pred_boxes


def save_video(video_path, save_path, draw_pred=False, pred_boxes=None,
               draw_opt=False, opt_boxes=None):
    """
    保存视频，可以在视频上绘制预测框和估计框

    :param video_path: 视频路径
    :param save_path: 视频保存位置，以 .avi 结尾
    :param draw_pred: 是否绘制预测框
    :param pred_boxes: 每一帧的预测框
    :param draw_opt: 是否绘制卡尔曼滤波器的估计框
    :param opt_boxes: 每一帧的估计框
    """
    cap = cv2.VideoCapture(video_path)  # 从指定路径加载视频
    fourcc = cv2.VideoWriter_fourcc(*'XVID')  # 保存格式为 .avi
    out = cv2.VideoWriter(save_path, fourcc, 25, (852, 480))  # 保存视频文件

    frame = 0
    while True:
        success, img = cap.read()
        if not success:
            break
        # 决定是否绘制预测框
        if draw_pred:
            if pred_boxes[frame] is not None:
                box = [round(i) for i in pred_boxes[frame]]
                cv2.rectangle(img, box[:2], box[2:], color=(218, 69, 0), thickness=2)
        # 决定是否绘制估计框
        if draw_opt:
            if opt_boxes[frame] is not None:
                box = [round(i) for i in opt_boxes[frame]]
                cv2.rectangle(img, box[:2], box[2:], color=(81, 154, 218), thickness=2)
        out.write(img)  # 保存视频文件
        frame += 1
        cv2.imshow('1', img)
        cv2.waitKey(1)

    cap.release()
    out.release()
    cv2.destroyAllWindows()


def convert_bbox_to_z(bbox):
    """
    将预测框从格式为 [x_min, y_min, x_max, y_max] 变换为 [cx, cy, s, r] 形式，
    其中 cx, cy 是预测框的中心坐标，s 是预测框的面积，r 是预测框的宽高比

    :param bbox: 代表 [x_min, y_min, x_max, y_max] 的列表
    :return: 改变格式后的列表
    """
    w = bbox[2] - bbox[0]
    h = bbox[3] - bbox[1]
    x = bbox[0] + w / 2.
    y = bbox[1] + h / 2.
    s = w * h  # 面积
    r = w / float(h)
    return np.array([x, y, s, r]).reshape((4, 1))


def convert_x_to_bbox(x):
    """
    将方框从 [cx, cy, s, r] 的格式转变为 [x_min, y_min, x_max, y_max] 的形式，
    该函数与 convert_bbox_to_z 相反

    :param x: 代表 [cx, cy, s, r, ...] 的列表，只会用到前面4个值
    :return: 改变格式后的列表
    """
    w = np.sqrt(x[2] * x[3])
    h = x[2] / w
    return np.array(
        [x[0] - w / 2., x[1] - h / 2., x[0] + w / 2., x[1] + h / 2.]
    ).reshape((1, 4))


class KalmanBoxTracker(object):
    """
    使用卡尔曼滤波对预测框进行优化
    """

    def __init__(self, bbox):
        self.kf = KalmanFilter(dim_x=7, dim_z=4)
        # 设置状态转移矩阵
        self.kf.F = np.array(
            [[1, 0, 0, 0, 1, 0, 0],
             [0, 1, 0, 0, 0, 1, 0],
             [0, 0, 1, 0, 0, 0, 1],
             [0, 0, 0, 1, 0, 0, 0],
             [0, 0, 0, 0, 1, 0, 0],
             [0, 0, 0, 0, 0, 1, 0],
             [0, 0, 0, 0, 0, 0, 1]]
        )
        # 设置状态向量到测量值的转换矩阵
        self.kf.H = np.array(
            [[1, 0, 0, 0, 0, 0, 0],
             [0, 1, 0, 0, 0, 0, 0],
             [0, 0, 1, 0, 0, 0, 0],
             [0, 0, 0, 1, 0, 0, 0]]
        )
        # 设置测量噪声的协方差矩阵 R
        self.kf.R[2:, 2:] *= 10.
        # 设置先验误差的协方差矩阵 P
        self.kf.P[4:, 4:] *= 1000.  # 对不可观测的初始速度给予高度不确定性
        self.kf.P *= 10.
        # 设置过程噪声的协方差矩阵 Q
        self.kf.Q[-1, -1] *= 0.01
        self.kf.Q[4:, 4:] *= 0.01
        # 设置初始状态，即使用初始预测框作为初始状态
        self.kf.x[:4] = convert_bbox_to_z(bbox)

    def update(self, bbox):
        # 跟预测框（测量值）进行更新
        self.kf.update(convert_bbox_to_z(bbox))

    def predict(self):
        # 面积是大于0的，如果小于0，就将面积的改变速度置为0
        if self.kf.x[6] + self.kf.x[2] <= 0:
            self.kf.x[6] = 0
        # 预测阶段
        self.kf.predict()
        return convert_x_to_bbox(self.kf.x)

    def get_state(self):
        # 获取当前的估计框
        return convert_x_to_bbox(self.kf.x)


def kalman_opt(boxes):
    opt_boxes = []  # 保存每一帧的估计框
    kbt = KalmanBoxTracker(boxes[0])
    for i in range(len(boxes)):
        # 如果该帧没有检测到，则估计框也为None
        if boxes[i] is None:
            opt_boxes.append(None)
            continue
        kbt.predict()
        kbt.update(boxes[i])
        # 保存当前帧的估计值
        opt_boxes.append(list(kbt.get_state()[0]))
    return opt_boxes


if __name__ == '__main__':
    pred_boxes = load_pred_boxes('../assets/boxes.txt')
    opt_boxes = kalman_opt(pred_boxes)

    # 仅在视频上绘制预测框
    # save_video('../assets/1.mp4', '../assets/pred.avi',
    #            draw_pred=True, pred_boxes=pred_boxes,
    #            draw_opt=False, opt_boxes=None)

    # 仅在视频上绘制估计框
    # save_video('../assets/1.mp4', '../assets/opt.avi',
    #            draw_pred=False, pred_boxes=None,
    #            draw_opt=True, opt_boxes=opt_boxes)

    # 在视频上同时绘制预测框（蓝色）和估计框（橙色）
    save_video('../assets/1.mp4', '../assets/cmp.avi',
               draw_pred=True, pred_boxes=pred_boxes,
               draw_opt=True, opt_boxes=opt_boxes)