前言

研一写的第一篇是fsQCA+NCA的组态分析实证论文，在此篇对软件操作及注意事项、论文实证分析部分的写作范式进行一个总结。

fsQCA方法主要参考张放fun的B站视频教程。
NCA方法主要参考南博吉吉的知乎文章。
论文实证分析部分的写作范式为杜运周老师的两篇《管理世界》论文，知网下载即可。

[1]杜运周、刘秋辰、程建青：《什么样的营商环境生态产生城市高创业活跃度？——基于制度组态的分析》，《管理世界》，2020年第9期。
[2]杜运周、刘秋辰、陈凯薇、肖仁桥、李姗姗：《营商环境生态、全要素生产率与城市高质量发展的多元模式——基于复杂系统观的组态分析》，《管理世界》，2022年第9期。

1 软件操作步骤

规范的操作步骤应当是按照论文实证分析部分写作的标准顺序来，如下：

1. 使用fsQCA软件，对处理好的数据进行校准，并另存为csv，手动将0.5改为0.499或0.501，再次导入软件，作为初始数据；
2. 对初始数据进行NCA的必要性水平检验；
3. 进行NCA的瓶颈水平分析；
4. 进行fsQCA的必要性检验；
5. 进行真值表操作，设置频数、一致性水平和PRI一致性水平，进行反事实分析，得出高和非高组态结果；
6. 稳健性检验。

但实际操作过程中，可能会因为结果不太理想，需要对数据进行多次的再处理，必要性检验的结果每次都会变但不会有太大变化。所以为图简便，推荐的操作步骤顺序如下：

1. 使用fsQCA软件，对处理好的数据进行校准，并另存为csv，手动将0.5改为0.499或0.501，再次导入软件，作为初始数据；
2. 对初始数据用fsQCA软件进行一次必要性检验，防止数据一开始的必要性就太强，随后的数据操作不会产生太大影响，因此不必每次换数据就重新做一遍；
3. 进行真值表操作，设置频数、一致性水平和PRI一致性水平，进行反事实分析，得出高和非高的组态结果；
4. 稳健性检验；
5. 进行fsQCA的必要性检验；
6. 进行NCA的必要性水平检验；
7. 进行NCA的瓶颈水平分析。

本文第2节第3节按推荐顺序安排，第4节按标准顺序安排。

2 fsQCA方法的详细操作步骤

2.1 软件下载

软件在张放fun的B站视频教程里有，可以在里面下载。

fsQCA的软件没有安装包，将压缩包解压后，点击fsqca.exe即可直接进入软件开始使用。

如果软件下载不到，也可以评论邮箱，我看到就把软件打包发过去，只有40M左右。

2.2 数据的准备

• 第一行的标题名需要用英文命名。
• 数据必须是纯数字，里不能有空格。
• 前因变量如果量纲不同，需要进行事先的max-min标准化，一般选择[0,100]区间。
• 需要将若干个前因变量和一个结果变量放在同一个表格中。
• 搜集数据时使用excel，全部搜集完毕后另存为csv格式。
• fsQCA软件点击File–>Open，选择csv文件即可打开数据。

2.3 校准点的确定

校准点的选择主要是根据出来的组态结果进行灵活调整，最常用的是90-50-10和75-50-25，对应称之为完全隶属-交叉点-完全不隶属，中间还会有85-50-15和80-50-20，一般是从90开始校准，结果满意直接一步到位，不满意依次向下用85、80、75，一般不能取到75以下。越往下，校准时出现的1和0就越多。

完全隶属和完全不隶属一般要关于交叉点对称，可能某些论文交叉点选择的不是50分位数，大多是较早的文章，但目前QCA逐渐成为范式，还是要选用50的。

2.4 变量的校准步骤及闪退问题

1. 使用excel的percentile()函数计算每个变量各个校准点的分位数，最后一个变量输入0.9表示90分位数，其他同理，示例如下。
   

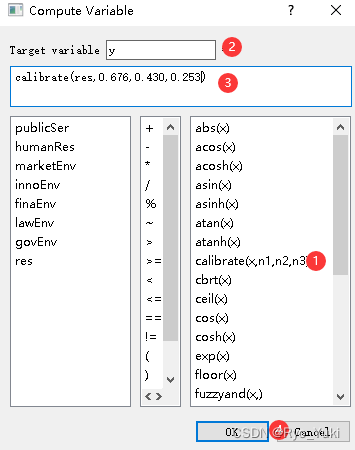
2. fsQCA软件点击Variables–>Compute–>右侧找到并点击calibrate（图中①）–>x处选择变量，n1、n2、n3输入为完全隶属、交叉点、完全不隶属的分位数值，上面的框（图中②）填入校准后的变量名（如x1、x2…y）–>点击OK。
   

3. 重复操作2，直至完成对每个变量的校准。

4. File–>Save as–>自定义个文件名，我一般定为“calibrated_905010.csv”–>打开另存为的csv文件，对x1、x2…y每个变量进行排序操作，将0.5改为0.499或0.501（QCA会将0.5的数据抛弃，这样改是为了不损失辛辛苦苦找来的数据）。

5. 将改好后的csv再次导入fsQCA软件，完成校准。

在这一步，很容易出现软件闪退的情况，基本上都是数据或操作上的问题，目前我碰到的和了解到的可能存在的问题有：

• 如果是第一次就闪退，检查整个数据文件的标题是否为非英文、是否有没标题的列，是否在没标题的列有数据；当然也可能就是第一列有问题，参照下一种。
• 如果是某一列数据闪退，可以将问题定位在该列数据，检查该列数据是否有空格，是否有文本格式，或是出现数字100或0的极端情况，也有可能是间隔过大（如最大的数是99，第二大的蹦到了60）。
• 还有一种可能，分位数输入错误，典型的就是把小数点点错位置。

2.5 fsQCA的数据必要性检验（开始一次+最后一次）

使用2.4中已经校准好的数据，点击Analyze–>Necessary Conditions–>①处outcome处选择y的高，②处Add Condition选择x，点击③处箭头添加–>重复上述步骤，将全部x的高和非高依次添加进去–>点击OK。

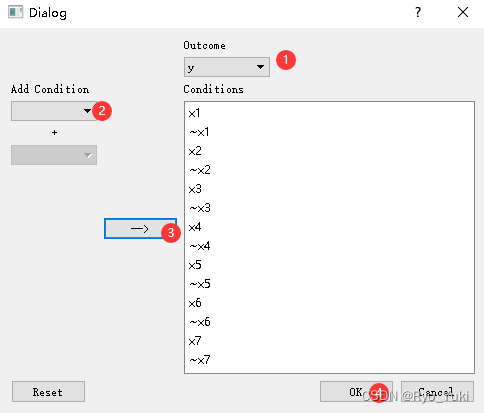
结果如下图所示，左边表示必要性一致性水平，右边表示覆盖度，前者均小于0.9且没有负值就表示非必要条件，结果通过。

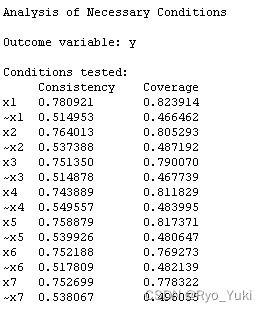
2.6 频数、一致性水平、PRI一致性水平的确定

该步骤为2.7做准备。在做高和非高时，三者的取值尽量保持一样，但如果实在组态结果不好，应该是可以做点改变的。

2.6.1 频数的确定

频数是指每种组态的个数，在真值表中number列的数字可以看到，小于设定的频数的组态将被忽略。

频数也需要根据出来的组态结果进行灵活调整，一般来说数据量上百了，频数要设定为2，如果出来的组态太多了，可以继续往上，不需要额外解释；如果组态太少，可以往下取1，可以做出适当解释，下图为杜运周等（2022）中关于频数选择为1的解释。

2.6.2 一致性水平、PRI一致性水平的确定

一致性水平具体表达的含义不是很清楚，在真值表中raw consist表示一致性水平，PRI consist表示PRI一致性水平。

有个不成文的规定，前者需要定在0.8以上，后者需要在0.7以上，如果不行可能就要面临重做。具体的选择也需要根据出来的组态结果进行灵活调整。

2.7 真值表操作步骤

Analyze–>Truth Table Algorithm（或直接使用快捷键Ctrl+T）–>选择y，点击①为高，②为非高，高和非高要分开做–>将x全部用③Add进去–>勾选④的作用是在输出组态的同时输出对应的典型案例，平时可以不用勾选，确定一切都成功后最后一次勾上即可–>OK。

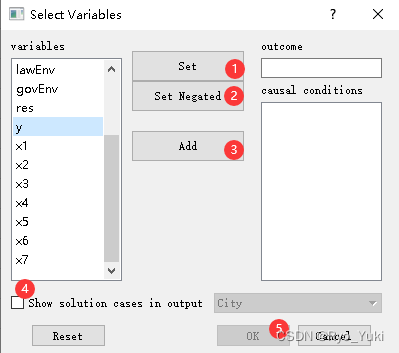
Edit–>Delete and Code（或直接使用快捷键Ctrl+D）–>①处输入频数，默认为1；②处输入一致性水平，默认0.8，点击OK后会发现，真值表按照一致性水平进行了降序排序，并且将所有大于设定值且频数大于等于设定值的组态的y列设置为1–>点击PRI consist 使其降序排序，将所有低于设定值的组态的y列手动修改为0。

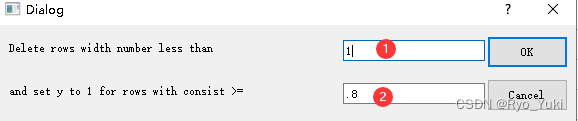
2.8 反事实分析

反事实分析一般来说可以和杜运周老师那两篇一样不去管，除非是能够确定单个变量一定可以影响结果变量的时候才做出选择。

点击真值表最右下方的Standard Analyse–>点击Select All–>默认为存在或确实，可以有根据得进行选择后，点击OK。

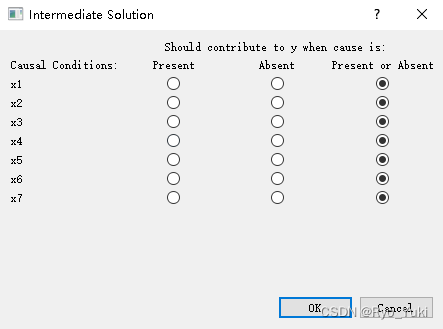
2.9 组态结果的评价与选择

以上步骤完成后，fsQCA软件的初始页面右侧输出框就会出现COMPLEX SOLUTION（复杂解）、PARSIMONIOUS SOLUTION（简单解）和INTERMEDIATE SOLUTION（中间解）。

一般不会去管复杂解，中间解处所展示的即为组态分析的最终结果，对照简单解结果，确定中间解的每条组态都能在其中找到对应，出现在简单解中的变量即为核心条件，没有则为边缘条件。

可能会出现多个组态对应一个简单解，在杜运周等（2020）中就有这样的情况（详见其论文里的S1a、S1b），说明核心条件相同，结果可以通过。

一般来说高的组态至少要有3个，不然组态结果太单薄；非高的组态不要多于高的组态，否则在组态评价时不好阐述。

另外还需要关注中间解的那些数据。raw coverage为原始覆盖度，unique coverage为唯一覆盖度，consistency为一致性水平，solution coverage为总体覆盖度，solution consistency为总体一致性水平。

一般来说总体一致性水平最好不要太低，最好要有个0.8往上。

3 NCA方法的详细操作步骤

3.1 R软件下载与NCA包的激活

详见南博吉吉的知乎文章（一）、（二）部分，此篇不过多介绍。

3.2 数据准备

NCA使用的数据目前没有明确的标准，杜运周老师的两篇论文也没有明确是用的哪种数据，因此可以用校准前的数据，也可以用校准后的数据（推荐，因为上文2.5里的QCA必要性检验用的是校准后的），对于某一种数据过不去的时候可以考虑。

另外，数据最好去掉最左侧的列名，方便操作，只保留若干个前因变量和一个结果变量数据，并另存为csv格式。如果去掉了第一列变量名，下方读取数据时需要设置header=False。

3.3 必要性水平检验

3.3.1 方法选择

必要性分析有两种，分别是上限回归（CR）和上限包络（CE），一般需要同时进行两种计算结果，杜运周老师的论文也是同时列出两种。如果适合自己数据的方法成功，另一个不成功也说的过去，用相关文献做支撑即可。

CR用于分析连续变量和超过5个的离散变量，CE分析二分变量和不到5个的离散变量。

3.3.2 非必要条件的认定

NCA检验的是必要条件，但是组态分析的论文进行NCA的目的是要验证每个变量都不是导致结果变量的必要条件，因此，所有变量均为非必要条件即可视为NCA通过。

非必要条件的认定条件为：效应量（d）<0.1或 显著性水平（P）>0.01 或前二者均满足。

3.3.3 具体操作步骤

假设数据第1列为结果变量，第2-8列为前因变量。

1. library(NCA)
   导入NCA包。
2. data<-read.csv(filepath,header=FALSE)
   filepath为文件所在路径的字符串，例如“C:\\Users\AUSU\\Desktop\\finalNCA.csv”，注意需要有两个\，因为程序语言里\一般为转义字符，多加一个\是使其保留\的属性。
   如果保留了第一列变量名，则不需要加header，否则需要加header=False。
3. model<-nca_analysis(data,X,Y,ceilings=“cr_fdh”, test.rep=10000)
   此处X处依次填入前因变量所在列的序号，Y处填入结果变量所在列的序号，如下图计算的是处在第1列的结果变量和处在第3列的前因变量的结果。将“cr_fdh”替换为“ce_fdh”，即可改为ce方法。
4. nca_output(model, test=TRUE)

5. 重复4，直至将全部的前因变量都进行必要性分析。
6. 指标记录后汇总后制表。
   Effect size 为d值，p-value为P值，此二者为判定非必要条件认定的关键。celling为上限区域，scope为范围，c-acctury为精确度。

3.4 瓶颈水平分析

假设数据第1列为结果变量，第2-8列为前因变量。

1. model <- nca_analysis (data,c(X1:X7),Y)
   根据假设，X1为2，X7为8，Y为1。
2. nca_output(model, summaries=FALSE, bottlenecks=TRUE)
   即可输出使用CR和CE两种方法进行分析的瓶颈水平结果。

4 论文写作范式

QCA中文论文的写作范式是杜老师的两篇《管理世界》的论文，在此简单总结。

4.1 校准点的选择与描述（研究设计章节末）

参考两篇论文的研究设计的章节末，写明实际使用的完全隶属、交叉点、完全不隶属选择的分位数点，并写明0.500的样本归属问题，通常改为0.501或0.499，并绘制一张表格将每个变量各个分位点的实际数据和描述性统计进行汇报。

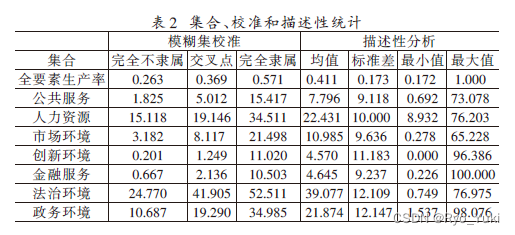
4.2 必要性分析

4.2.1 基于NCA的必要性分析

说明使用的方法、得到的变量和非必要条件的判定情况，并绘制表格汇报以上结果。

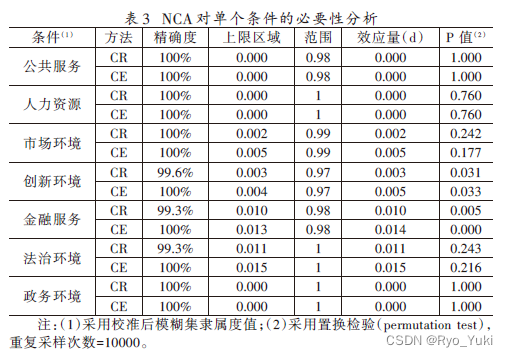
4.2.2 瓶颈水平分析

选择一个层级的结果变量水平，举例说一下达到该层级的高需要百分之多少的每个前因变量的程度即可。将NCA输出的结果绘制表格即可。

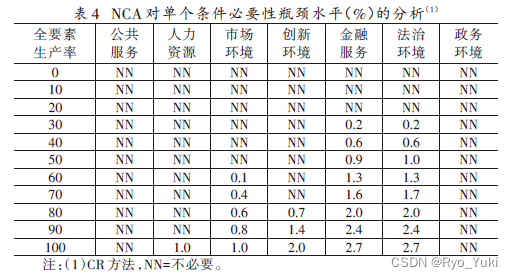
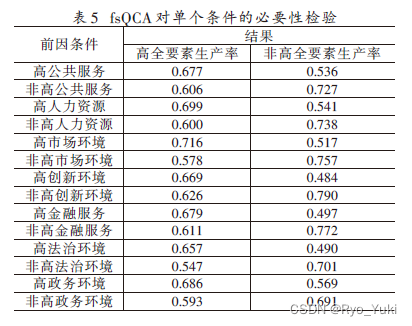
4.2.3 基于QCA的必要性分析

绘制QCA必要性分析的结果表格，并说明一下非必要条件的判定条件。

4.3 充分性分析（即组态分析）

4.3.1 绘制表格

模仿杜老师的表格绘制方法绘制，大实心圆表示核心条件存在，小实心圆表示边缘条件存在，大圈差表示核心条件确实，小圈差表示边缘条件缺失。下方的数据也会在fsQCA软件中输出，具体的判定方法见本文2.9部分。

4.3.2 高组态的命名、介绍、举例及定性论证

一般来说论文都是分析产生高组态的原因，对组态进行命名并对命名原则进行陈述，举个典型例子对该组态的驱动机制进行定性的分析，映证机制分析部分对组态驱动机制的描述。

4.3.3 非高组态的简单介绍

非高组态一般不是分析的重点，但需要有，简单介绍一下即可。

4.4 稳健性分析

小幅改变频数、一致性水平、PRI一致性水平、校准点，只要不变化或者变化得不是太大都视为结果稳健。