一、说明

根据L.R Rabiner等人[1]的说法，隐马尔可夫模型是一个双重嵌入的随机过程，其潜在的随机过程是不可观察的（它是隐藏的），但只能通过另一组产生观察序列的随机过程来观察。

基本上，隐马尔可夫模型（HMM）是观察一系列排放，但不知道模型生成排放所经历的状态序列的模型。我们分析隐马尔可夫模型，以从观察到的数据中恢复状态序列。听起来很混乱吧...

二、马尔可夫过程

2.1 马尔可夫模型和马尔可夫链

要理解HMM，我们首先需要了解什么是马尔可夫模型。马尔可夫模型是一种随机模型，用于对伪随机变化状态进行建模。这意味着当前状态不依赖于以前的状态。最简单的马尔可夫模型是马尔可夫链。在这种情况下，当前状态仅取决于上一个状态。

2.2 什么是HMM和马尔可夫链......

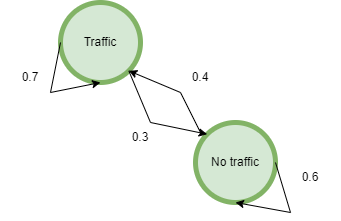
Rob 参加了一个游戏，在该游戏中，飞镖击中靶心后会颁发奖品。奖品保存在屏幕后面的 3 个不同的盒子（红色、绿色和蓝色）中。现在，分发奖品的人会根据他早上是否被堵在交通中来发放奖品。这些称为状态。现在，由于 rob 知道该地区交通的总体趋势，他可以将其建模为马尔可夫链。但是他没有任何关于交通的确切信息，因为他无法直接观察它们。他们对他是隐藏的。他也知道奖品将从绿色、红色或蓝色的盒子中挑选出来。这些称为观察。由于他无法观察到状态和观测结果之间的相关性，因此该系统是HMM的系统。

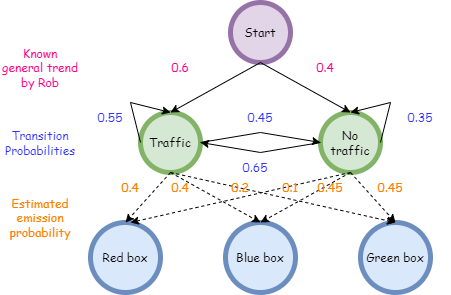
2.2.1 转移概率

转移概率是从一种状态移动到另一种状态的概率。在这种情况下，如果今天我们有流量，明天有 55% 的可能性会有流量，明天有 45% 的可能性没有流量。同样，如果我们今天没有流量，明天有 35% 的可能性没有流量，明天有 65% 的可能性会有流量。

2.2.2 排放概率

它们是观察者可以观察到的输出概率。在这里，连接状态和观测值的概率是发射概率。

HMM 在 python 中的表示

三、HMM的基本结构

正如我们之前所讨论的，隐马尔可夫模型具有以下参数：

隐藏状态集（M）
交易概率矩阵（A）
一系列观测值（t）
发射概率矩阵（也称为观测似然）（B）
参数的初始概率分布

3.1 HMM 的核心问题

评估

第一个问题是找到观察到的序列的概率。

译码

第二个问题是找到最可能的隐藏状态序列——维特比算法、正向-后向算法

学习

第三个问题是找到最大化观测数据可能性的参数——鲍姆-韦尔奇算法

3.2 关于HMM的假设

马尔可夫假设

由于HMM是马尔可夫模型的增强形式，因此以下假设成立：未来状态将仅依赖于当前状态。

它表示如下：

3.2.1 马尔可夫假设

输出独立性

输出观测值（oi）的概率仅取决于产生观测值的状态，而不取决于任何其他状态或任何其他观测值。它表示如下：

3.2.2 输出独立性

前向算法

让我们有一个简单的HMM，我们有两个隐藏的状态，它们代表一个城镇的天气，我们也知道一个孩子，他可以根据天气携带两样东西中的任何一个，一顶帽子和一把雨伞。孩子的物品与天气之间的关系由橙色和蓝色箭头显示。黑色箭头表示状态的过渡。

图片来源：作者

假设我们知道以下项目序列

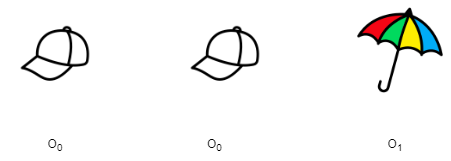
一个序列

我们使用前向算法来查找观察到序列的概率，给定HMM的参数是已知的，即转移矩阵，发射矩阵和平稳分布（π）。

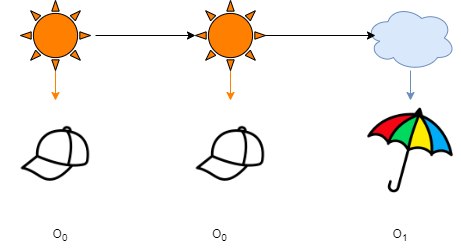
具有潜在隐藏状态的序列

我们找到了所有可能的隐藏状态，这些状态可能导致我们进入这个序列。我们找到每个序列的累积概率。我们发现总共有 8 个这样的序列。现在计算每个序列的概率将是一项繁琐的任务。直接计算联合概率需要对所有可能的状态序列进行边缘化，其数量随着序列长度的增加呈指数增长。相反，前向算法利用隐马尔可夫模型的条件独立规则以递归方式执行计算。

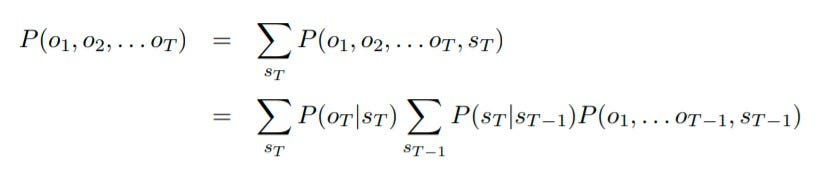
序列的概率

序列的概率是隐藏状态的所有可能序列的总和，可以表示为上述。

递归地表示如下，其中 t 是序列的长度，s 表示隐藏状态。

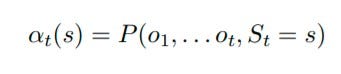
概率的递归表达式

例如，如果 t=1，

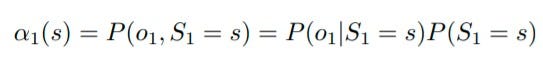
现在，为了得到最终答案，我们找到每个隐藏状态的α t并将其相加。它表示如下：

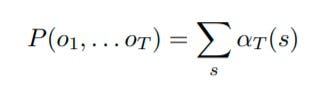
前向算法的最终表达式

在前向算法中，我们使用当前时间步的计算概率来推导出下一个时间步的概率。因此，它在计算上更有效。

前向算法主要用于需要我们在知道观察序列时确定处于特定状态的概率的应用程序。我们首先计算为上一个观测值计算的状态的概率，并将其用于当前观测值，然后使用转移概率表将其扩展到下一步。该方法缓存所有中间状态概率，因此仅计算一次。这有助于我们计算固定状态路径。该过程也称为后验解码。

3.3 逆向算法

后向算法是正向算法的时间反转版本。在逆向算法中，我们需要找到机器在时间步 t 处处于隐藏状态并生成序列剩余部分的概率。在数学上，它表示为：

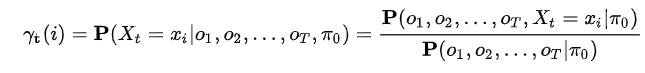
3.4 正向-后向算法

正向-后向算法是一种推理算法，用于计算所有隐藏状态变量（分布）。此推理任务通常称为平滑。该算法利用动态规划原理，高效计算两次获得后验边际分布所需的值。第一遍在时间上前进，而第二遍在时间上倒退;因此得名正向-后向算法。它是上面解释的正向和后向算法的组合。该算法计算给定 HMM 的观察序列的概率。该概率可用于对识别应用中的观察序列进行分类。

四、维特比算法

对于包含隐藏变量的 HMM，确定哪个变量序列是某些观察序列最有可能的基础源的任务称为解码任务。解码器的任务是在有经过训练的模型和一些观察到的数据时找到最佳隐藏序列。更正式地说，给定作为输入 a 作为 A 和 B 和一个观察序列 O = o₁， o₂， ...， ot，找到最可能的状态序列 S = s₁， s₂， . . . .圣。

我们当然可以使用前向算法来找到所有可能的序列，并在最大可能性上选择最好的序列，但这无法做到，因为存在指数级数量的状态序列。

与前向算法一样，它估计 vt（j）在看到第一个 t 观测值并通过最可能的状态序列 s₁、s₂、. .圣。每个单元格 vt（ j）的值是递归计算的，采用可能将我们引向该单元格的最可能路径。形式上，每个单元格表示以下概率

我们可以通过一个例子更好地理解这一点，

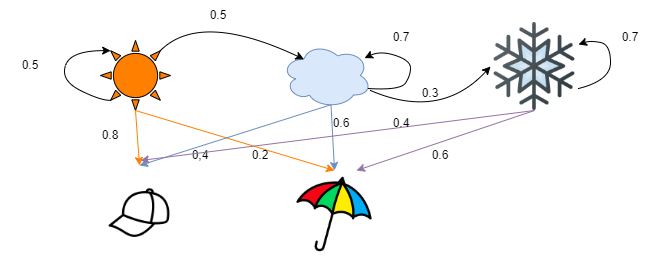
五、HMM 模型

假设我们有一个 HMM 模型，如图所示。我们总是从太阳（x），云（y）开始，以雪（z）结束。现在，您已经观察了前向算法问题中的序列。生成此路径的最可能的序列是什么？

选项包括：

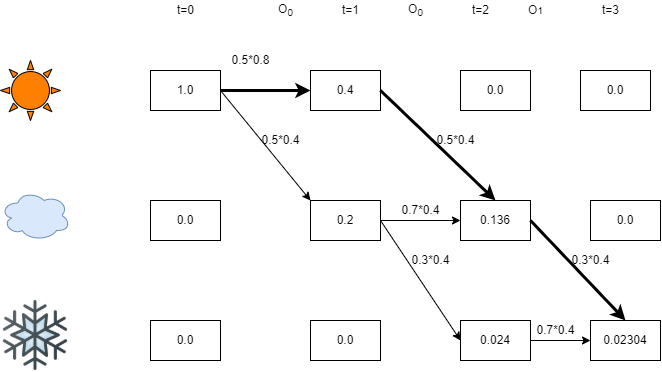
手动计算

在这种情况下，粗体路径是维特比路径。当您从上一个状态返回时，您可以看到这一点：0.3*0.4*0.136 > 0.7*0.4*0.024

同样，0.4*0.5*0.4 > 0.7*0.4*0.2

因此，最可能的序列是 xxyz。

请注意，可以有多个可能的最佳序列。

由于每个状态仅取决于之前的状态，因此您可以逐步获得最可能的路径。在每一步中，您都会计算最终进入状态 x、状态 y、状态 z 的可能性。在那之后，你是如何到达那里的并不重要。

六、鲍姆-韦尔奇算法

该算法为“在什么参数化下观察到的序列最有可能？

鲍姆-韦尔奇算法是期望最大化（EM）算法的一个特例。它利用前向-后向算法来计算特定步骤的统计信息。其目的是调整HMM的参数，即状态转移矩阵，发射矩阵和初始状态分布。

从过渡和发射矩阵的随机初始估计开始。
计算每个跃迁/发射的使用频率的预期。我们将估计潜在变量 [ ξ， γ ]
根据这些估计值重新计算跃迁和发射矩阵的概率。
重复直到收敛

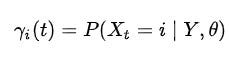
潜在变量γ的表达式

γ是给定观察到的序列 Y 和参数 theta 时处于状态 i 的概率

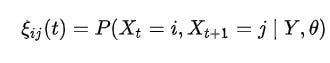
潜在变量 ξ 的表达式

ξ 是给定观察到的序列 Y 和参数 theta 时处于状态 i，j 的概率

参数（A， B）更新如下

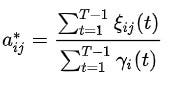
更新 A 或转换矩阵

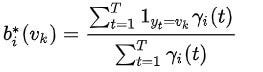
更新 B 或发射矩阵

七、HMM的优势

NLP中使用的HMM标记器训练起来非常简单（只需要从训练语料库中编译计数）。
性能相对较好（命名实体的性能超过 90%）。
它消除了标签偏差问题
由于每个 HMM 仅使用正数据，因此它们可以很好地扩展;因为可以在不影响学习的 HMM 的情况下添加新单词。
我们可以初始化模型，使其接近被认为是正确的。

八、HMM的缺点

为了定义观察和标签序列的联合概率，HMM需要枚举所有可能的观察序列。
表示多个重叠要素和长期依赖关系是不切实际的。
要评估的参数数量巨大。因此，它需要一个大型数据集进行训练。
HMM，训练涉及最大化属于类的示例的观察到的概率。但它并没有最小化观察其他类实例的概率，因为它只使用正数据。
它采用了马尔可夫假设，该假设不能很好地映射到许多现实世界的域

九、隐马尔可夫模型在哪里使用？

分析生物序列，特别是DNA[2]
时间序列分析
手写识别
语音识别[1]

如果您想阅读有关该主题的更多信息，请提供一些链接：

https://youtube.com/playlist?list=PLM8wYQRetTxBkdvBtz-gw8b9lcVkdXQKV
https://www.cs.cmu.edu/~aarti/Class/10701_Spring14/slides/HMM.pdf

参考和引用

[1] L. R. Rabiner，“隐马尔可夫模型教程和语音识别中的选定应用”，载于 IEEE 论文集，第 77 卷，第 2 期，第 257–286 页，1989 年 10 月，doi：1109.5/18626.2。
[22]什么是隐马尔可夫模型？Nat Biotechnol 1315， 1316–2004 （10）.https://doi.org/1038.1004/nbt1315-<>