目录
一、背景知识
1.1 理想时序模型
1.2 实际时序模型
1.2.1 时钟不确定性
1.2.2 触发器特性
二、时序分析
2.1 时序模型图
2.2 时序定性分析
一、背景知识
之前的章节提到,时钟对于FPGA的重要性不亚于心脏对于人的重要性,所有的逻辑运算都离开时钟的驱动。那是不是只要有时钟就可以正常运行?答案是否定的,时钟是不能随意的,一个工程设计是否逻辑正常,还需要有正确的时序分析结果。
1.1 理想时序模型
对于一个信号电平1要从寄存器FF1传输到FF2,波形如右图,CLK1成为发送时钟,CLK2为捕获时钟,本例中发送时钟和捕获时钟来自相同的时钟源,实际可不同。在clk1的上升沿位置,信号开始传入,然后从Q直接输出,输出波形为FF1_Q,在第二个周期,电平1要被CLK2的上升沿捕获从而从FF2的Q输出,波形为FF2_Q。
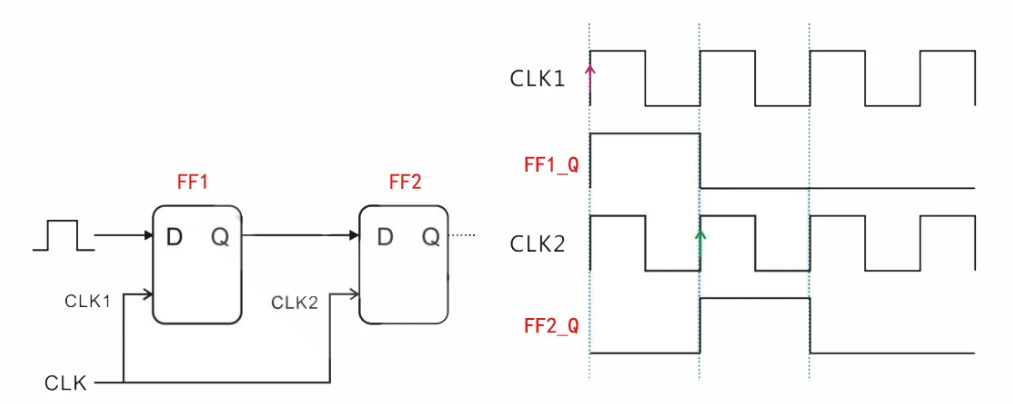
时序分析,即分析两个寄存器间的时序效果,提到时序就离不开你无法忽视而且必须理解透彻的4个概念:setup建立时间、holdup保持时间、recovery恢复时间、removal去除时间。信号可分为3类:时钟信号,控制信号,数据信号,控制信号又包括使能信号,复位信号。setup/holdup描述的是时钟信号和数据信号的关系,recovery/removal描述的是时钟信号和复位信号的关系。
1.2 实际时序模型
在实际的模型中,有两个重点考虑的因素:时钟,触发器
1.2.1 时钟不确定性
时钟存在不确定性,包括时钟时延,时钟偏斜,时钟抖动
时钟时延:时钟在线路上传输存在时延
时钟偏斜:时钟经过不同路径到达寄存器的时间不同,存在时间差,即为时钟偏斜
时钟抖动:时钟的频率无法保持任何时刻间都完全一致,存在变化,这种变为称为时钟抖动
时钟边沿切换:理想的时钟信号,在上升沿和下降沿状态的切换是瞬间完成的,实际上上升沿和下降沿是一个变化的过程,也是需要一定的时间。
1.2.2 触发器特性
触发器从逻辑功能上分为RS触发器,D触发器,JK触发器,从触发形式也可分为边沿触发和电平触发。根据触发器的真值表可明确看出区别,在实际使用时主要都是D触发器,D触发器也是由RS触发器改造而成的。D触发器自身特性是导致存在setup和holdup的根本原因,下图为边沿触发的D触发器内部结构图,由6个与非门组成。
输入为CLK和D,有F4和F5的输出反馈回到F3和F6的输入,而这其中,就存在一定的要求:在时钟上升沿到来前,数据需提前到达,提前到达的最小时间为setup时间,这样数据D才能有效被捕获到,此外,数据和时钟依次到达后,数据信号还需稳定一段时间,该时间的最小值即为holdup时间,否则触发器的输出将不可预知。
注:setup和holdup时间为器件的硬件特性,也即该值为固定值,时序分析时两值为常数。

二、时序分析
2.1 时序模型图
以触发器FF1到触发器FF2间的时序路径为例进行分析,可抽象为下图流程。

clk1:启动时钟,数据data存入FF1
clk2:捕获时钟,FF2用clk2进行Q1的输出数据,为方便理解,clk1和clk2为周期相同的同步时钟
Td:数据data传输到FF1输入端口D1的传输时延Td
Tclk1:时钟clk1传输到FF1时钟端口的时延
Tco:数据data从FF1的输入端口D1到输出端口Q1的时延,也即FF1数据处理时间
Tcomb:数据从Q1到D2中组合逻辑处理的时延
Tnet:数据从Q1到D2中传输过程中的线路传输时延
Tclk2:时钟clk2传输到FF2时钟端口的时延
Tsetup:触发器FF2的建立时间,数据如果要从D2端口被FF2稳定检测到,则要比时钟clk2边沿至少提前Tsetup到达
Tholdup:触发器FF2的保持时间,数据如果要从D2端口被FF2捕获到,则在时钟clk2边沿到达后还得维持状态至少Tholdup时间后,数据才真正被FF2存储进去
T:clk1和clk2的时钟周期相同,都为T,周期不同的分析类似。
2.2 时序定性分析
时钟分析原则:在一个时钟周期内,捕获寄存器FF2上,数据到达时间要比时钟提前至少Tsetup,在时钟到达后,数据至少要保持状态Tholdup时长的时间才能准确存入寄存器中。
时钟波形图如下图
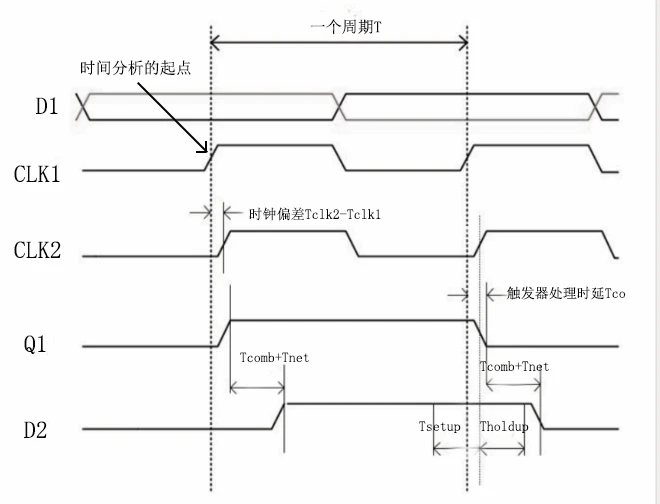
数据到达时间:Tdata=Tclk1+Tco+Tcomb+Tnet
时钟到达时间:Tclk=T+Tclk2
建立时间满足条件:Tsetup<=T+Tclk-Tdata=T+Tclk2-(Tclk1+Tco+Tcomb+Tnet)
公式变换:T>=Tco+Tcomb+Tnet+Tsetup+Tclk1-Tclk2
公式含义:数据传输时延+时钟偏斜+setup时间需小于等于一个周期的时间
保持时间满足条件:Tholdup<=Tdata-Tclk=Tclk1+Tco+Tcomb+Tnet-Tclk2
公式变换:Tclk1+Tco+Tcomb+Tnet>=Tclk2+Tholdup
公式含义:数据从触发器FF1传输到触发器FF2的时延小于等于FF2的时钟延时加上holdup时间,因为对FF2来说,数据data从FF1到达FF2的D端口后,维持Tdata后即会被下一个data覆盖。
对于setup公式还有一个容易引起疑问的地方,就是setup时间到达时间加上了一个时钟周期T,这个要注意波形图中标注的分析的时间起点,最终setup、holdup是针对数据D1从FF1传输到FF2的输入端口D2后进行的,数据从D1到Q1是需要耗费一个周期,因此需要增加一个周期T。
另外,对于modelsim仿真的波形会发现时钟上升沿和数据的变化有时是完全对齐的,无需考虑保持时间和建立时间,这是因为仿真的波形为理想的波形。











![【PWN · ret2text | 伪rand()】[HDCTF 2023]pwnner](https://img-blog.csdnimg.cn/339edd02df01402e9c7e30a1541e879e.png)