题目描述
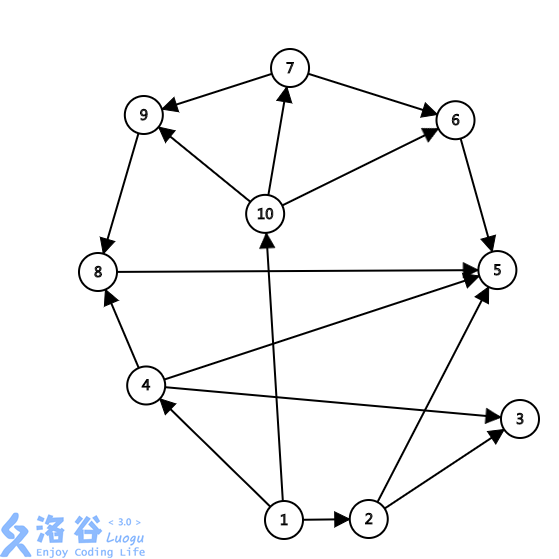
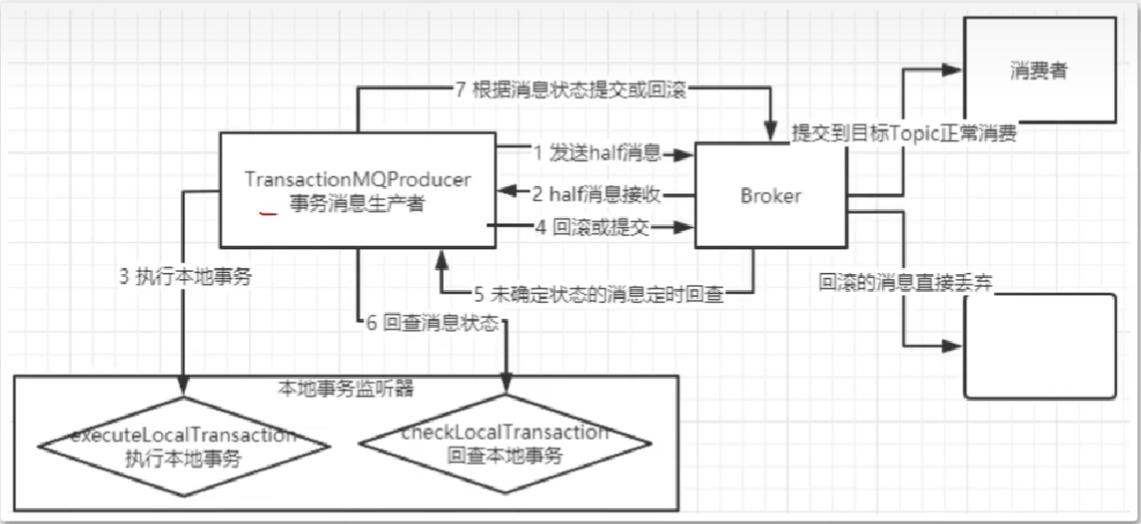
如图所示为某生态系统的食物网示意图,据图回答第 1 小题
现在给你 n 个物种和 m 条能量流动关系,求其中的食物链条数。物种的名称为从 1 到 n 编号 M 条能量流动关系形如 1,2,3,…,am−1,bm−1,am,bm。其中 ai 和 bi 表示能量从物种 ai 流向物种 bi,注意单独的一种孤立生物不算一条食物链。
输入格式
第一行两个整数 n,m,接下来 m 行每行两个整数 ai 和 bi 描述 m 条能量流动关系。
输出格式
一个整数即食物网中的食物链条数。
输入输出样例
输入 #1复制
10 16 1 2 1 4 1 10 2 3 2 5 4 3 4 5 4 8 6 5 7 6 7 9 8 5 9 8 10 6 10 7 10 9
输出 #1复制
9
说明/提示
数据保证输入数据符号生物学特点,且不会有重复的能量流动关系出现,题目保证答案不会爆 int。
对于 100%100% 的数据,1≤N≤100000,1≤m≤200000。
记忆化搜索
warn:first[x]==0 (出度为0)
#include<bits/stdc++.h>
using namespace std;
//#pragma GCC optimize(2)
#define endl '\n'
#define lowbit(x) ((x)&-(x))
const int mod=1e9+7;
typedef long long ll;
ll ans=0,n1,m1;
ll t,s1,s2,s3,s4,max1=0,min1=100000000,sum=0,n,m,i,j,k,l,r;
ll u,v,w;
inline int read() {
bool sym=0;
int res=0;
char ch=getchar();
while(!isdigit(ch))sym |=(ch =='-'),ch=getchar();
while(isdigit(ch)) res =(res<<3)+(res<<1)+(ch^48),ch=getchar();
return sym ? -res : res;
}
void print(int x) {
if(!x)return;
print(x/10);
putchar(x%10+'0');
}
int isPrime(int n) {
float n_sqrt;
if(n==1) return 0;
if(n==2 || n==3) return 1;
if(n%6!=1 && n%6!=5) return 0;
n_sqrt=floor(sqrt((float)n));
for(int i=5; i<=n_sqrt; i+=6) {
if(n%(i)==0 | n%(i+2)==0) return 0;
}
return 1;
}
ll anss[205205];
ll dp[205205],first[205005],vis[200005],cnt=0;
struct node{
ll to,next,w;
}edges[400005];
void add(ll u,ll v){
edges[++cnt].to =v;
edges[cnt].next =first[u];
first[u]=cnt;
}
ll dfs(ll x,ll fa){//没什么用的 fa
cout<<" "<<first[x]<<" ";
if(first[x]==0&&vis[x]!=0)
return 1; //first[x]的妙用;(出度为0)(即为一条链);vis[x]判断是1否孤立(是否为根节点)(即一个点)
if(anss[x])//这个x点若搜过,则直接返回,即剪枝
return anss[x];
for(ll i=first[x];i;i=edges[i].next){//遍历
ll v=edges[i].to ;
//if(v==fa)
// continue;
anss[x]=(anss[x]+dfs(v,x));
}
return anss[x];//记忆化搜索
}
ll root;
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
cin>>m;
for(i=1;i<=m;i++){
cin>>s1>>s2;
add(s1,s2);
//add(s2,s1);// 有向图
vis[s2]++;
}
for(i=1;i<=n;i++){
if(vis[i]==0)// 找根节点
{
ans+=dfs(i,-1);
}
}
cout<<ans;
return 0;
}
//mio lover