A - Rotate A - Rotate

题目大意

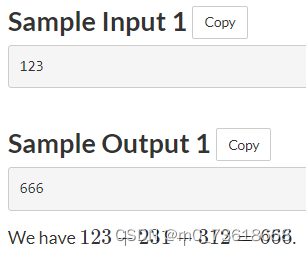
题目要求给定一个3位的整数abc，其中每个数字都不是0。计算abc + bca + cab的结果。

思路分析

• 将a、b和c按照题目要求的顺序连接起来，得到字符串abc、bca和cab。
• 将这三个字符串转换为整数，分别表示为变量abc_int、bca_int和cab_int。
• 计算abc_int + bca_int + cab_int的值，并将结果保存在变量ans中。

时间复杂度

O(logN)

AC代码

#include<bits/stdc++.h>
using namespace std;

int main() {
    char a, b, c;
    cin >> a >> b >> c;

    // 将字符连接成字符串
    string abc = string({a, b, c});
    string bca = string({b, c, a});
    string cab = string({c, a, b});

    // 将字符串转换为整数
    int abc_int = stoi(abc);
    int bca_int = stoi(bca);
    int cab_int = stoi(cab);

    int ans = abc_int + bca_int + cab_int;

    cout << ans << endl;

    return 0;
}

B - Climbing TakahashiB - Climbing Takahashi

题目大意

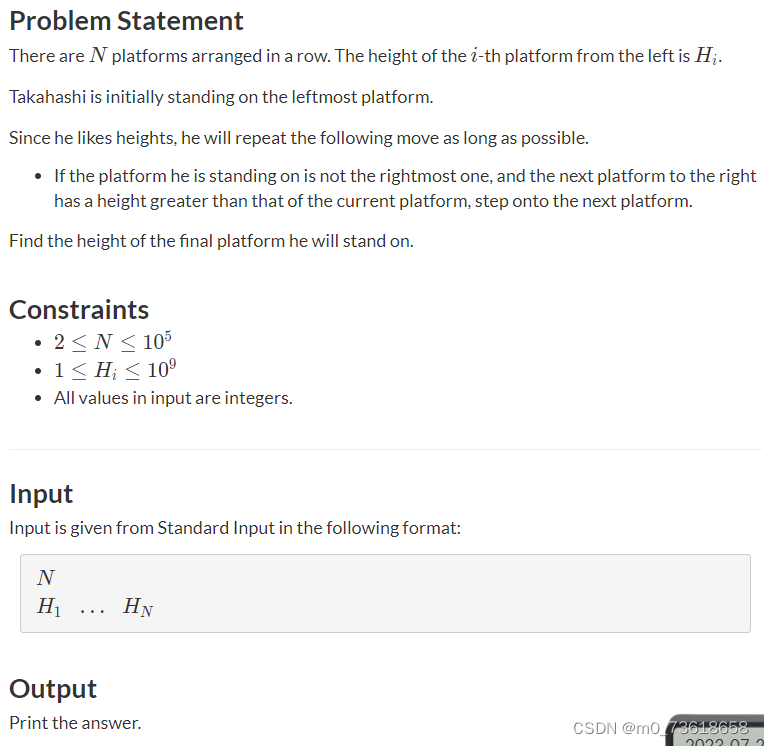
题目给出了N个平台的高度，Takahashi初始站在最左边的平台上。他会尽可能地向右移动，只要右侧的平台高度比当前平台高。要求找到他最终站在的平台的高度。

思路分析

遍历平台，如果当前平台高度大于等于下一个平台高度，则输出当前平台高度并结束程序。如果整个序列都满足升序条件，则输出最后一个平台的高度。

时间复杂度

O(N)

AC代码

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n;
    cin >> n; 
    vector<int> h(n);
    for (int i = 0; i < n; i++)
        cin >> h[i]; 

    for (int i = 0; i < n - 1; i++) {
        if (h[i] >= h[i + 1]) {
            cout << h[i] << endl;
            return 0; 
        }
    }
    cout << h[n - 1] << endl; 
    return 0;
}

C - The Kth Time QueryC - The Kth Time Query

题目大意

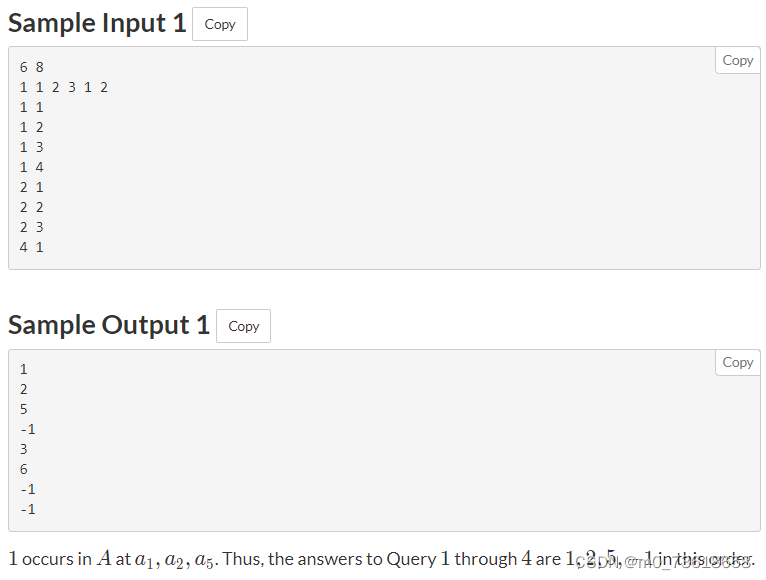
给定一个长度为N的整数序列A，以及Q个查询。每个查询包含一对整数(x, k)，表示在序列A中找到第k次出现的x，并输出其索引。如果不存在第k次出现的x，则输出-1。

思路分析

可以使用map来记录每个元素的出现次数和对应的索引，以便快速回答查询。通过将每个元素的出现次数和索引存储在map中，可以在O(1)时间内找到第k次出现的x。

时间复杂度

O(N+Q)

AC代码

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int n, q;
    cin >> n >> q;
    
    map<int, map<int, int>> m;
    vector<int> a(n);
    
    for(int i=0; i<n; i++)
    {
        cin >> a[i];
        int t = m[a[i]].size() + 1;
        m[a[i]][t] = i + 1;
    }
    
    while(q--)
    {
        int x, k;
        cin >> x >> k;
        
        if(m.find(x) != m.end() && k <= m[x].size())
            cout << m[x][k] << endl;
        else 
            cout << -1 << endl;
    }
    
    return 0;
}