给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2
示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842…, 由于返回类型是整数，小数部分将被舍去。

提示：

0 <= x <= 2³¹ - 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sqrtx
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

原理

牛顿法（数值分析中使用到的）:

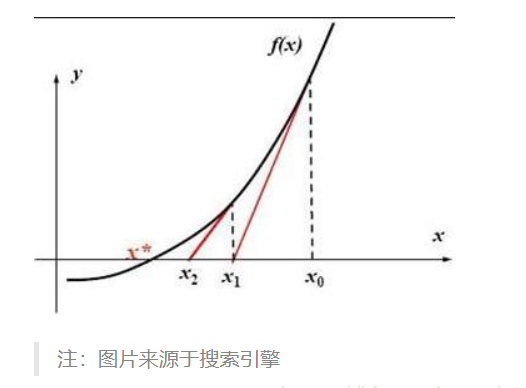
在迭代过程中，以直线代替曲线，用一阶泰勒展式（即在当前点的切线）代替原曲线，求直线与 xx 轴的交点，重复这个过程直到收敛。

首先随便猜一个近似值 xx，然后不断令x等于x和a/x的平均数，迭代个六七次后 xx 的值就已经相当精确了构造方程x − a² = 0，令f ( x ) = x − a ² ,然后不断用(x,f(x))的切线来不断逼近方程$x^{2} $
上述函数导数为2x，也就是说函数上任意一点(x,f(x))处的切线斜率为2x。

那么x-f(x)/(2x)就是一个比x更接近的近似值，代入f ( x ) = x ² − a 可以得到x − ( x² − a ) / ( 2 x )变形即可得到(x+a/x)/2 这里的a是目标值

二分法

这道题目由于只要求取开平方后的整数部分，因此搜索范围有限，可以考虑使用二分法。

构造数组从0到输入x，该数组中每个元素与其所在位置相等，定义两个指针，左指针left和右指针right，初始位置分别位于数组两端；

执行循环，循环的控制条件是左指针不能跑到右指针的右边去，每轮循环获得中点所在位置，查看该数的平方s与输入x之间的大小关系：
（1）s == x：相当于找到了开方结果，直接返回这个数；
（2）s > x：平方结果较大，删除数组右半部分
（3）s < x：平方结果较小，删除数组左半部分

跳出循环时，返回右指针所在位置。

解决方案

二分查找法应用于搜索平方根的思想很简单，其实就是“猜”，但是是有策略的“猜”，用“排除法”在有限的区间里，一次排除一半的区间元素，最后只剩下一个数，这个数就是题目要求的向下取整的平方根整数。

牛顿法最初提出的时候，是用于求解方程的根，它的基本思想是“以直代曲”，在迭代中搜索得到方程的近似解。

java 实现

实例

public class Solution {

    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        // 注意：针对特殊测试用例，例如 2147395599
        // 要把搜索的范围设置成长整型
        long left = 1;
        long right = x / 2;
        while (left < right) {
            // 注意：这里一定取右中位数，如果取左中位数，代码会进入死循环
            // long mid = left + (right - left + 1) / 2;
            long mid = (left + right + 1) >>> 1;
            long square = mid * mid;
            if (square > x) {
                right = mid - 1;
            } else {
                left = mid;
            }
        }
        // 因为一定存在，因此无需后处理
        return (int) left;
    }

}

执行结果

python 实现

实例

class Solution(object):
    def mySqrt(self, x):
        """
        :type x: int
        :rtype: int

        核心思想：
                1. 直接return int(sqrt(x)) 直接ac
                2. 使用暴力遍历方法 for i in range(1,x) 尝试 i*i 是否 == x 或者 i*i < x 但是 (i+1)(i+1) > x
                3. 使用牛顿法（数值分析中使用到的）:
                    在迭代过程中，以直线代替曲线，用一阶泰勒展式（即在当前点的切线）代替原曲线，求直线与 xx 轴的交点，重复这个过程直到收敛。
                    首先随便猜一个近似值 xx，然后不断令x等于x和a/x的平均数，迭代个六七次后 xx 的值就已经相当精确了

                    构造方程x - a^{2} = 0，令f(x)=x-a^{2},然后不断用(x,f(x))的切线来不断逼近方程x^{2}
                    上述函数导数为2x，也就是说函数上任意一点(x,f(x))处的切线斜率为2x。
                    那么x-f(x)/(2x)就是一个比x更接近的近似值，代入f(x)=x^{2}-a可以得到x-(x^{2}-a)/(2x)
                    变形即可得到(x+a/x)/2 这里的a是目标值
        """
        if x == 0:
            return 0
        cur_x = x # 令初始值为x
        while cur_x-x/cur_x > 1e-6:
            cur_x = (cur_x + x/cur_x)/2 # 利用公式(x+a/x)/2计算得到新的a
        return int(cur_x)

if __name__ == '__main__':
    s = Solution()
    print(s.mySqrt(8))