Problem - D - Codeforces

翻译：

有一张纸，可以用大小为𝑛×𝑚:𝑛行和𝑚列的单元格表示。所有的细胞最初都是白色的。

𝑞操作已应用到工作表。他们的𝑖-th可以描述如下:

𝑥𝑖𝑦𝑖-选择一个𝑘非白色和颜色的整个行𝑥𝑖和整个列𝑦𝑖。新颜色应用于每个单元格，而不管该单元格在操作之前是否被着色。
应用所有𝑞操作后的纸张称为着色。如果存在至少一个单元格以不同的颜色着色，则两种着色是不同的。

有多少种不同的颜色?打印数字模998244353。

输入
第一行包含一个整数𝑡(1≤𝑡≤104)——测试用例的数量。

测试用例的第一行包含四个整数𝑛、𝑚、𝑘和𝑞(1≤𝑛，𝑚，𝑘，𝑞≤2⋅105)——纸张的大小、非白色颜色的数量和操作的次数。

下面的𝑞行中的𝑖-th包含了对𝑖-th操作的描述—两个整数𝑥𝑖和𝑦𝑖(1≤𝑥𝑖≤𝑛;1≤𝑦𝑖≤𝑚)—操作应用到的行和列。

𝑞对所有测试用例的和不超过2⋅105。

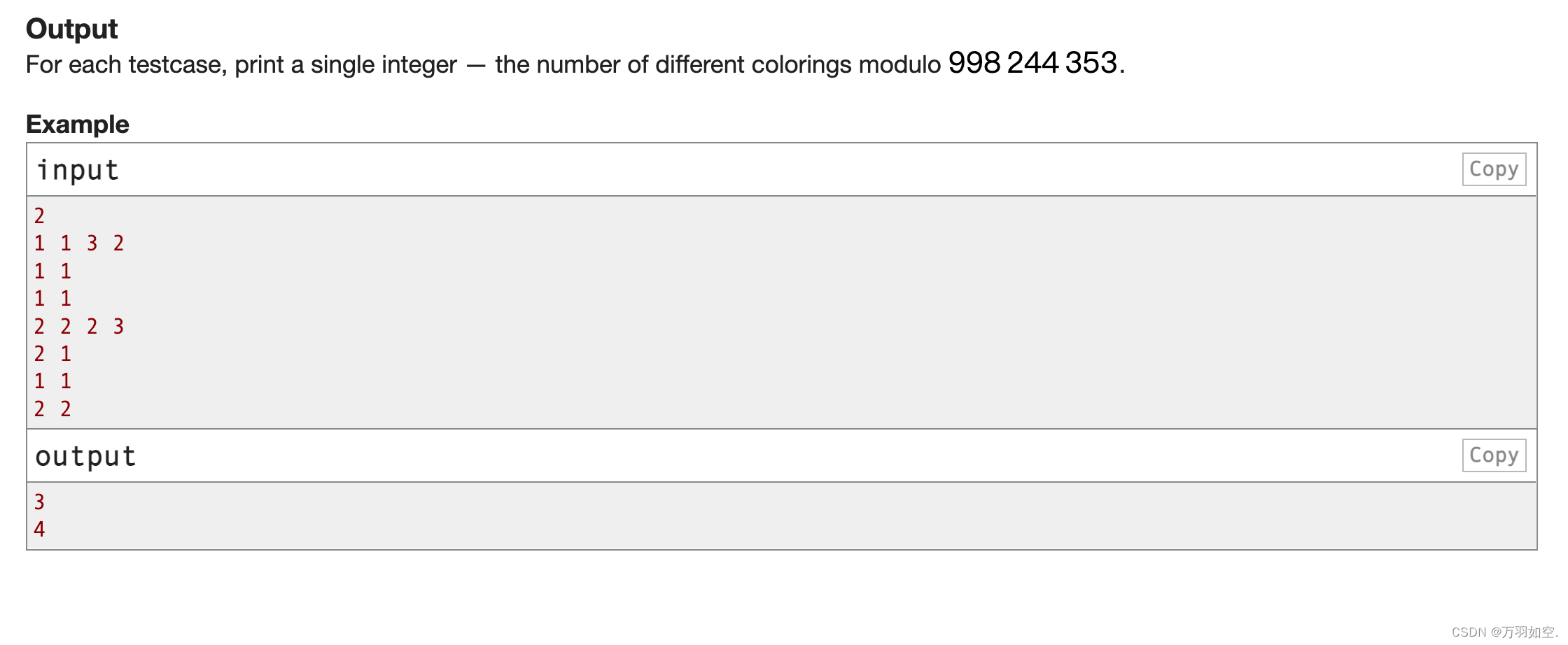
输出
对于每个测试用例，打印一个整数——对998244353模的不同颜色的数量。

例子
inputCopy
2
1 1 3 2
1
1
2 2 2 3
2 1
1
2 - 2
outputCopy
3.
4

思路：

根据已给的顺序来进行涂颜色，然后最后计算有多少种不同颜色的方案。正着模拟，我们就需要全部模拟一下，然后再bfs/dfs查找连通块的数量。数据范围过大会直接T掉。正难则反，我们倒着来的话，会发现我们只需要记录每行每列的数量就可以了，如果满足了行或者列就可以break，因为是最后涂的，所以不用担心被覆盖。

代码：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
const ll mod=998244353;
int m,k,q;
struct we{
    int x,y;
}c[200005];
bool h[200005],l[200005];
ll ksm(ll x,ll y){
    ll oper=1;
    while (y) {
        if (y&1) {
            oper=oper*x%mod;
        }
        x=x*x%mod;
        y>>=1;
    }
    return oper%mod;
}
void solv(){
    cin>>n>>m>>k>>q;
    
    for (int i =1; i<=n; i++) {
        h[i]=false;
    }
    for (int i =1; i<=m; i++) {
        l[i]=false;
    }
    
    for (int i=0; i<q; i++) {
        cin>>c[i].x>>c[i].y;
    }
    int na=0;
    int h1=0,l1=0;
    for (int i=q-1; i>=0; i--) {
        if (l1==m||h1==n) {
            break;
        }
        if (h[c[i].x]&&l[c[i].y]) {
            continue;
        }
        
        if (!h[c[i].x]) {
            h[c[i].x]=true;
            h1++;
        }
        if (!l[c[i].y]) {
            l[c[i].y]=true;
            l1++;
        }
        na++;
    }
    printf("%lld\n",ksm(k, na));
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}