【隐式动态求解】使用非线性纽马克方法的隐式动态求解研究（Matlab代码实现）

news2024/12/28 17:43:30

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

非线性纽马克方法（Nonlinear Newton-Raphson method）是一种用于求解非线性方程组的数值方法，其中包含了隐式动态求解的研究。该方法在许多科学和工程领域中都得到了广泛应用，特别是在动态系统模拟和求解过程中。

隐式动态求解是指在求解微分方程的过程中，将时间步长（时间离散）和求解方程（空间离散）同时进行。相比于显式动态求解方法，它更能应对复杂的非线性系统和高度非线性的方程。

在使用非线性纽马克方法进行隐式动态求解时，可以按照以下步骤进行：

1. 离散时间步长：将时间轴分成离散的时间步长，即给定初始时间和结束时间，并确定时间步长的大小。

2. 空间离散：将动态系统的方程进行空间离散，通常使用有限差分、有限元或其他数值近似方法。

3. 定义非线性方程组：将离散化后的动态系统的方程组表示为一个非线性方程组，其中未知数是各个离散点上的状态变量或变量值。

4. 应用非线性纽马克方法：使用非线性纽马克方法对非线性方程组进行迭代求解。这包括计算雅可比矩阵，更新解向量，直到收敛准则满足为止。

5. 时间迭代：在每个时间步长上，重复步骤2到步骤4，以求解每个时间点上的状态变量。

隐式动态求解具有较好的数值稳定性和收敛性，特别适用于求解高度非线性问题、刚性系统和对时间步长要求较高的情况。然而，它也可能会增加计算的复杂性和求解的计算量。

总的来说，使用非线性纽马克方法进行隐式动态求解可以得到更准确和稳定的结果，适用于涉及复杂非线性动态系统的仿真和求解问题。在实际应用中，需要根据具体问题的特点和要求来选择合适的数值方法和求解策略。

📚2 运行结果

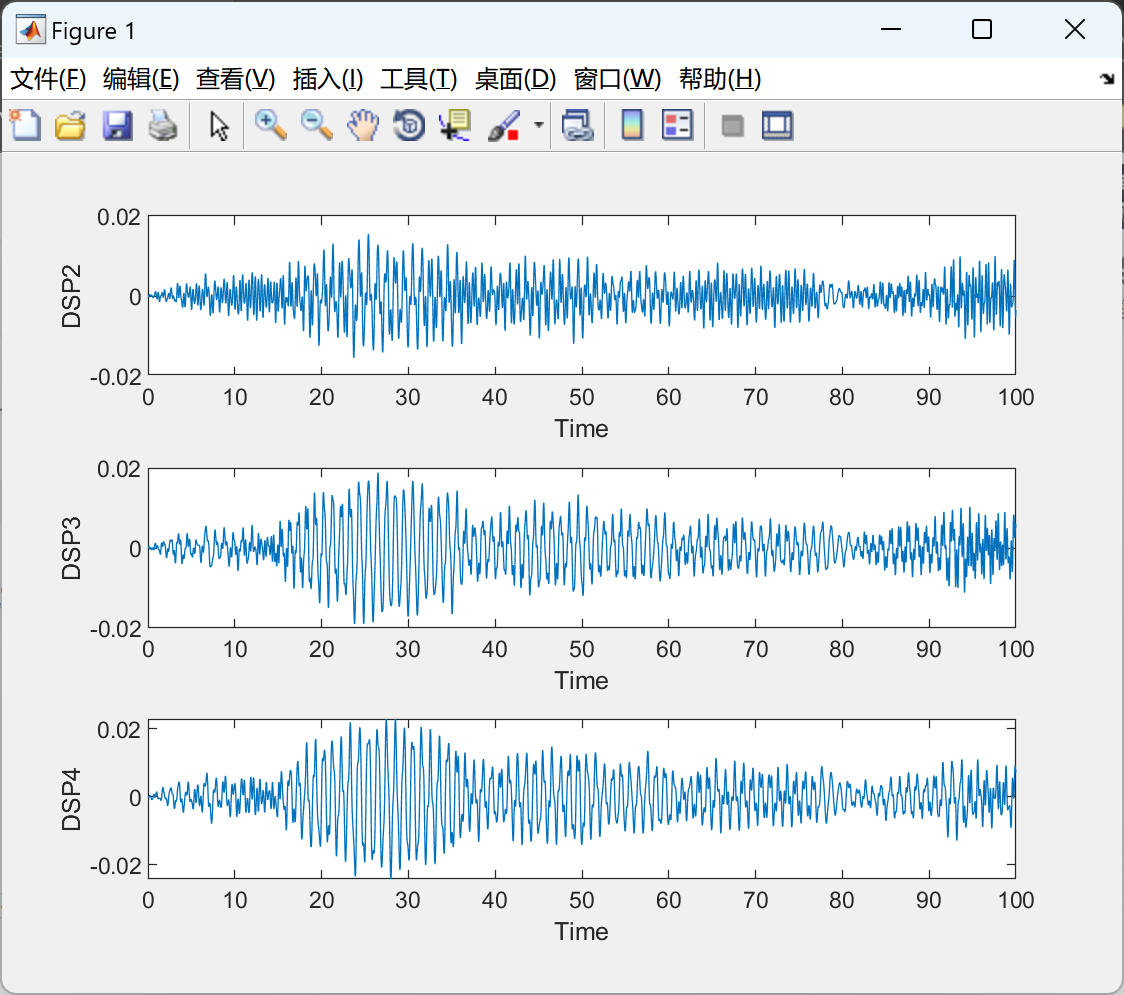
主函数代码：

clear; clc; close all;

%Input

M=5*diag(ones(3,1)); %Mass matrix
C=0.01*M; %Damping matrix
f=randn(3,10000); %force
fs=100; %Sampling frequency
delta=10e-4; %Convergance criterion for residual force

%Material types definition
Material{1}.k1=1000; %Spring stiffness
Material{1}.x1=0.01; %Spring deformation beyond which the stiffness decreases
Material{1}.k2=10; %Reduced stiffness

%Elements connectivity and material used
Elements{1}.DOFs=[1 2]; Elements{1}.Material=1;
Elements{2}.DOFs=[2 3]; Elements{2}.Material=1;
Elements{3}.DOFs=[3 4]; Elements{3}.Material=1;
%Support and Free DOFs
Support=[1]; Free=[2 3 4];

Result=Newmark_Nonlinear(Elements,Material,Support,Free,M,C,f,fs,delta);

t=[0:1/fs:9999/fs];
figure;
subplot(3,1,1);
plot(t,Result.Displacement(1,:)); xlabel('Time'); ylabel('DSP2');
subplot(3,1,2);
plot(t,Result.Displacement(2,:)); xlabel('Time'); ylabel('DSP3');
subplot(3,1,3);
plot(t,Result.Displacement(3,:)); xlabel('Time'); ylabel('DSP4');