论文标题：FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting
论文链接：
https://arxiv.org/abs/2201.12740
代码链接：
https://github.com/DAMO-DI-ML/ICML2022-FEDformer

摘要

尽管基于变压器的方法显著改善了长期序列预测的最新结果，但它们不仅计算成本高，更重要的是，无法捕捉时间序列的全局视图(例如总体趋势)。为了解决这些问题，我们提出将Transformer与季节趋势分解方法相结合，其中分解方法捕捉时间序列的全局轮廓，而Transformer捕捉更详细的结构。为了进一步提高Transformer的长期预测性能，我们利用了大多数时间序列倾向于在众所周知的基础上(如傅立叶变换)具有稀疏表示的事实，开发了频率增强Transformer。除了更有效之外，被称为频率增强分解变压器({f FEDformer})的方法比标准变压器效率更高，其复杂度与序列长度成线性关系。我们对6个基准数据集的实证研究表明，与最先进的方法相比，FEDformer在多变量和单变量时间序列中分别可以减少14.8%和22.6%的预测误差。

主要贡献

frequency enhanced decomposed Transformer
Fourier enhanced blocks and Wavelet enhanced blocks

模型结构

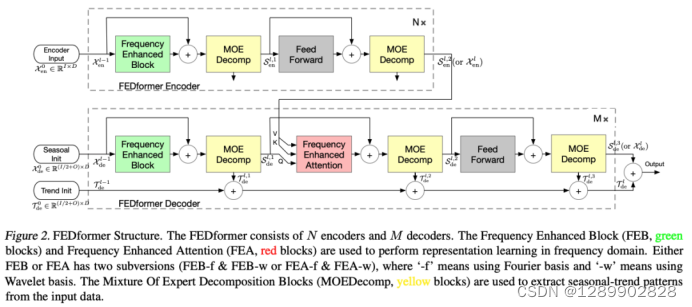
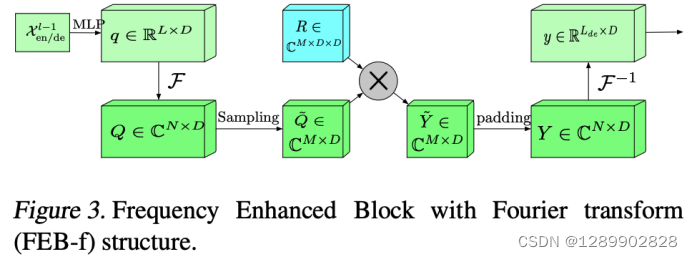
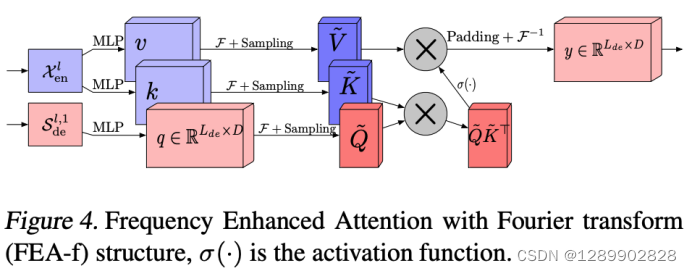
Frequency Enchanced Block（FEB）和 Frequency Enhanced Attention（FEA）具有相同的流程：频域投影 -> 采样 -> 学习 -> 频域补全 -> 投影回时域

无论多长的信号输入，模型只需要在频域保留极少的点，就可以恢复大部分的信息

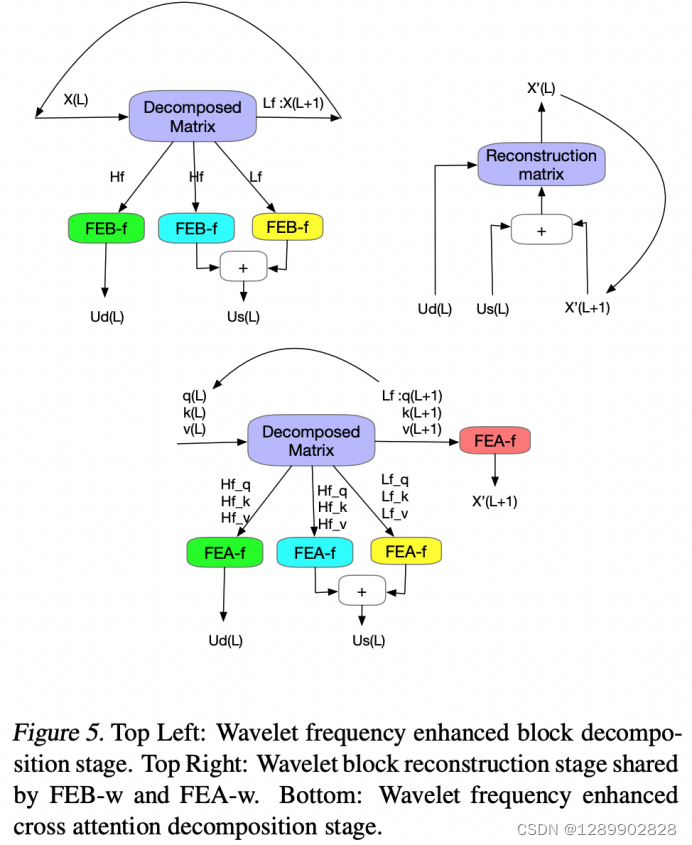
傅立叶基具有全局性而小波基具有局部性。小波版的 FEDformer 可以在更复杂的数据集上得到更优的效果。但小波版的 FEDformer 运行时间也会更长。

实验

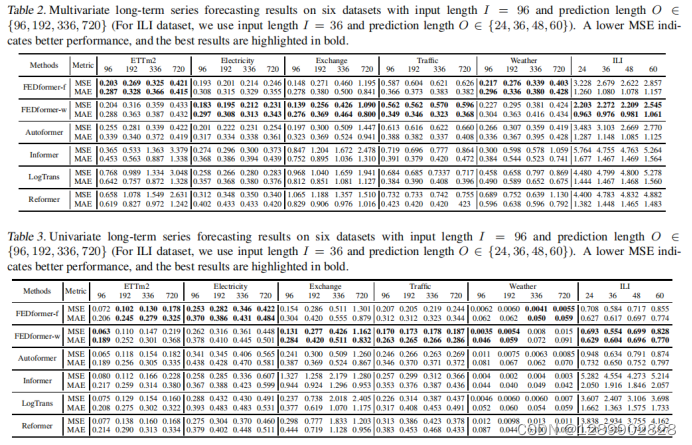
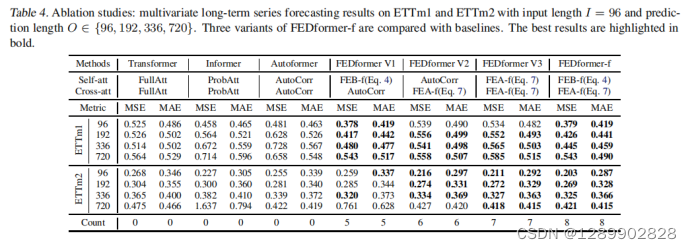
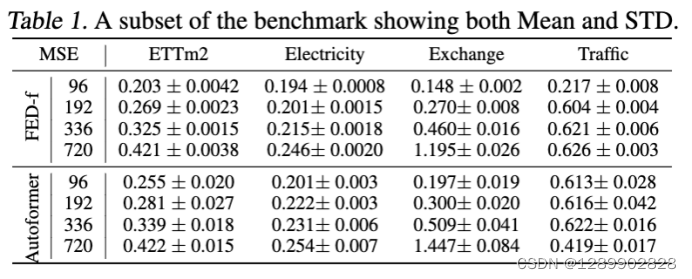
采样实验

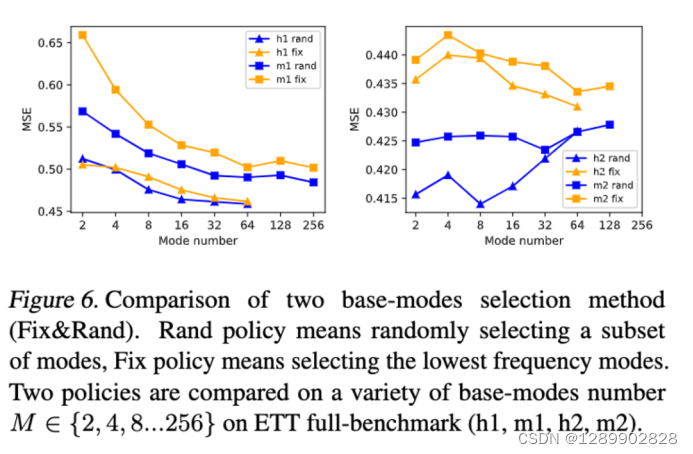
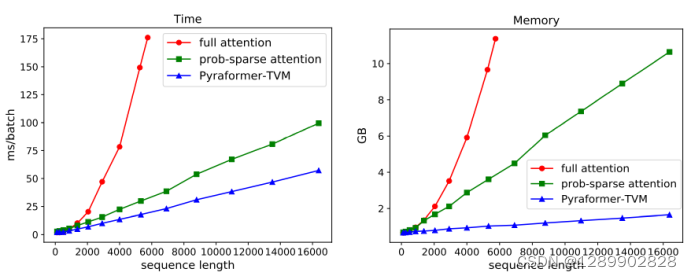
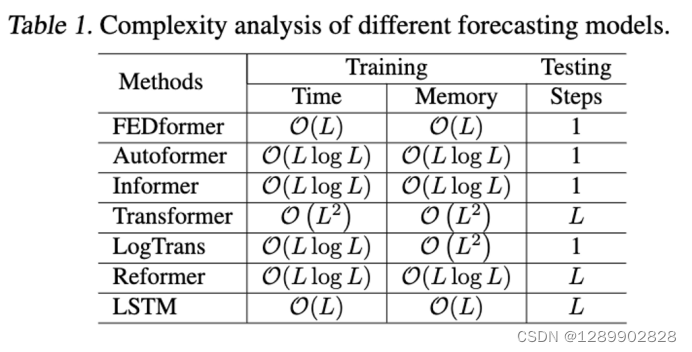
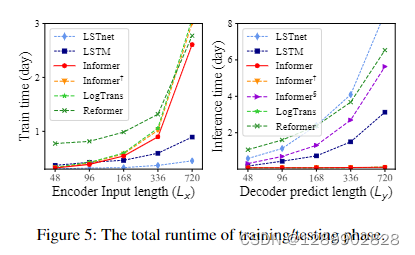
速度和内存

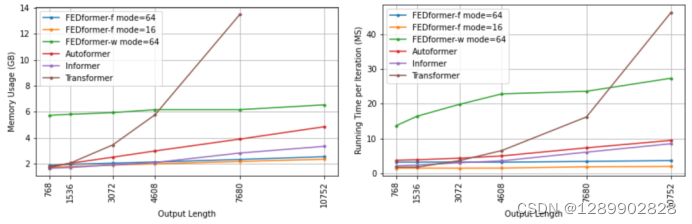
内存占用和运行时间比Informer和Autoformer还是要多一些的。

总结

针对长时间序列预测问题，提出了基于频域分解的 FEDformer 模型。大幅提高了预测精度和模型运行效率。提出了一种基于傅立叶/小波变换的模块，通过在频域进行固定数量的随机采样，使得模型达到线性复杂度同时提高精度。