0.1 学习视频源于:b站:刘二大人《PyTorch深度学习实践》
0.2 本章内容为自主学习总结内容,若有错误欢迎指正!
1 线性模型
1.1 通过简单的线性模型来举例:

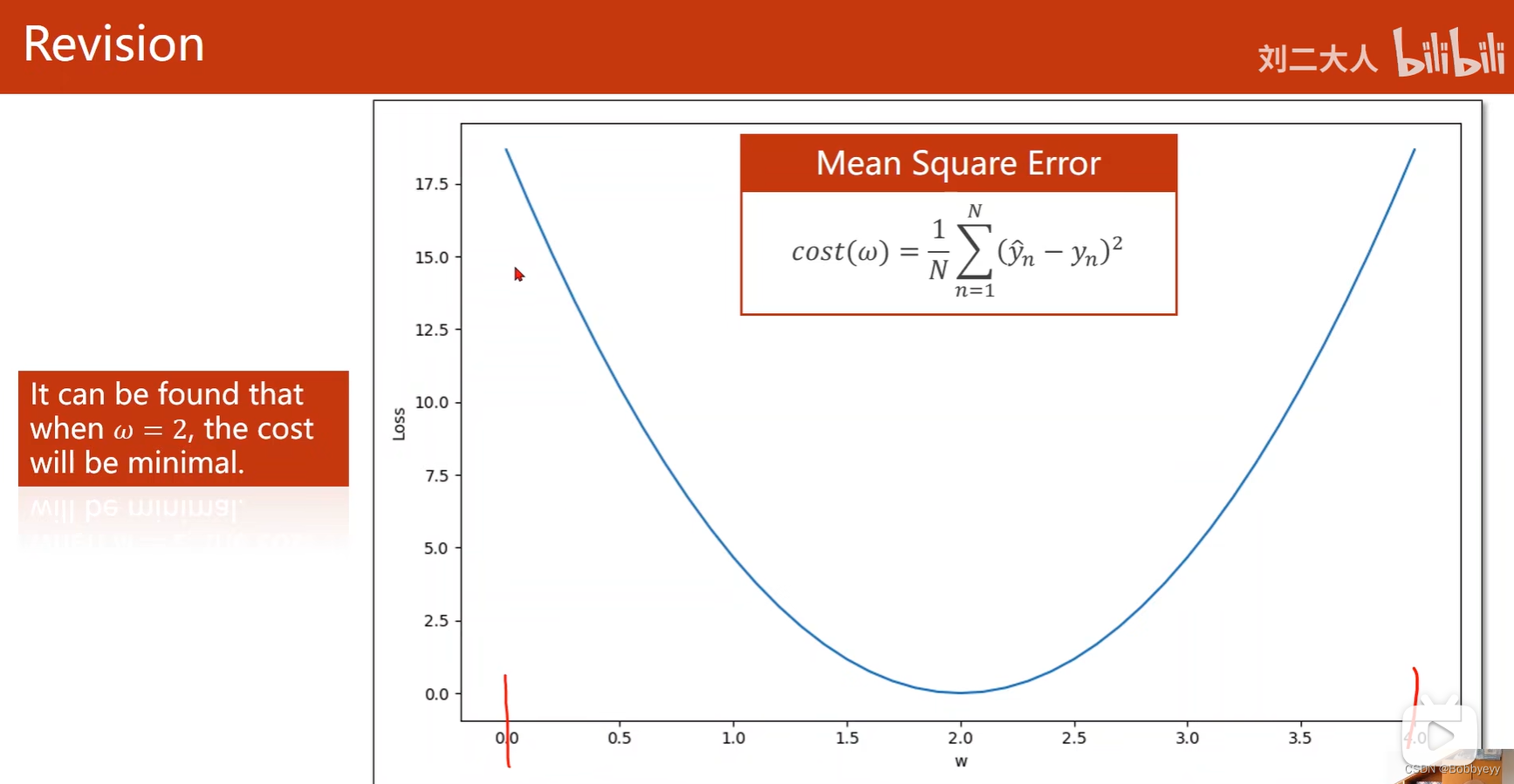
1.2 如图,简单的一个权重的线性模型,首先通过随机取w的值来找到与true line重合的w,其中通过MSE来判断w取值是否合理。(最简单的通过评价指标来判断模型的效果如何)
1.3 但是对于多个权重来说,搜索权重w的数量呈幂函数增长。此时可以想到分治方法,通过分治法减少首次搜索次数,找到MSE较小的点在进行一定区间范围内的权重w搜索。但是这种方法对于大部分的MSE曲线(不规则,非凸函数),会因为第一轮的分治取值不当导致错过最优点。
2 梯度下降
2.1 所以引入梯度下降算法寻找最小MSE值。
2.2 Q:什么是梯度?A:cost函数(本文为MSE)对权重求导。
2.3 梯度下降更新权重的方法:
(减去学习率×导数,是因为如果寻找的导数为负值,说明该区间曲线递减,则w向后取值即w数值增加;如果为正,说明该区间曲线递增,则w向前取值即w数值减少。学习率:一般取值不宜太大,其控制MSE曲线上所取的w的跨越程度,学习率取值太大容易导致cost函数发散。)
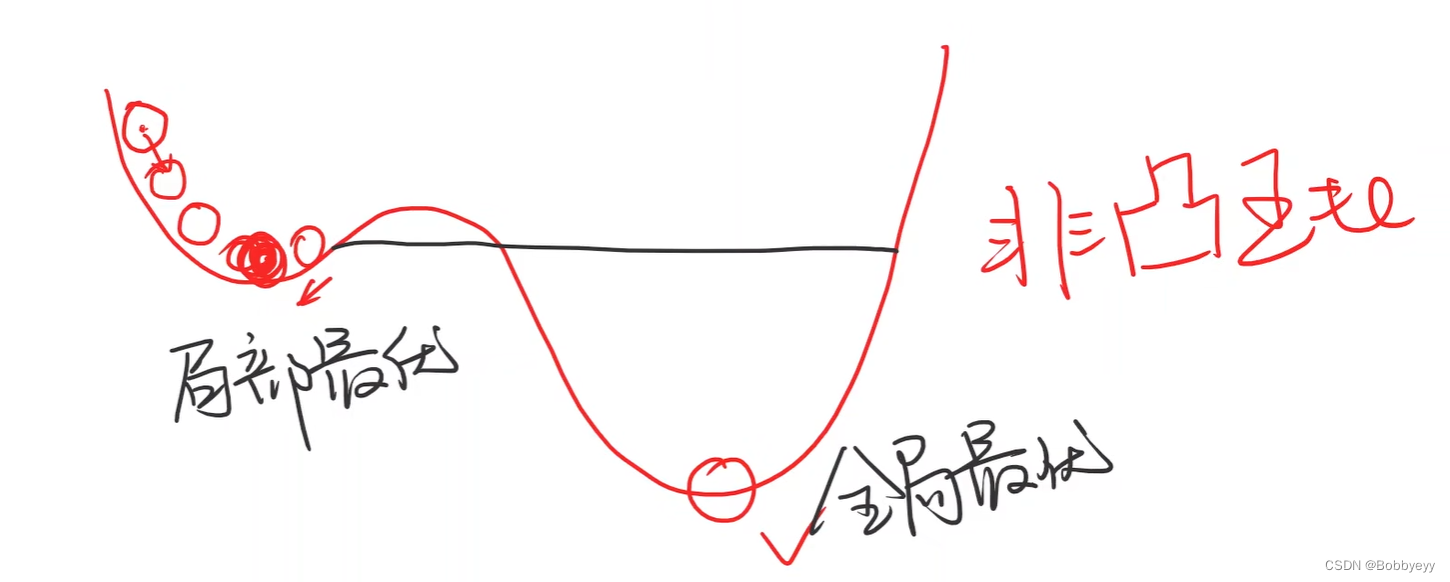
2.4 梯度下降为贪心算法,由于非凸函数存在多个最优点(局部最优),所以梯度下降算法很难找到全局最优,容易陷入局部最优点,但是在深度神经网络中并没有太多的局部最优点,即很难陷入局部最优,所以梯度下降算法依然被大量使用。同时梯度下降算法存在鞍点问题(梯度为0)。
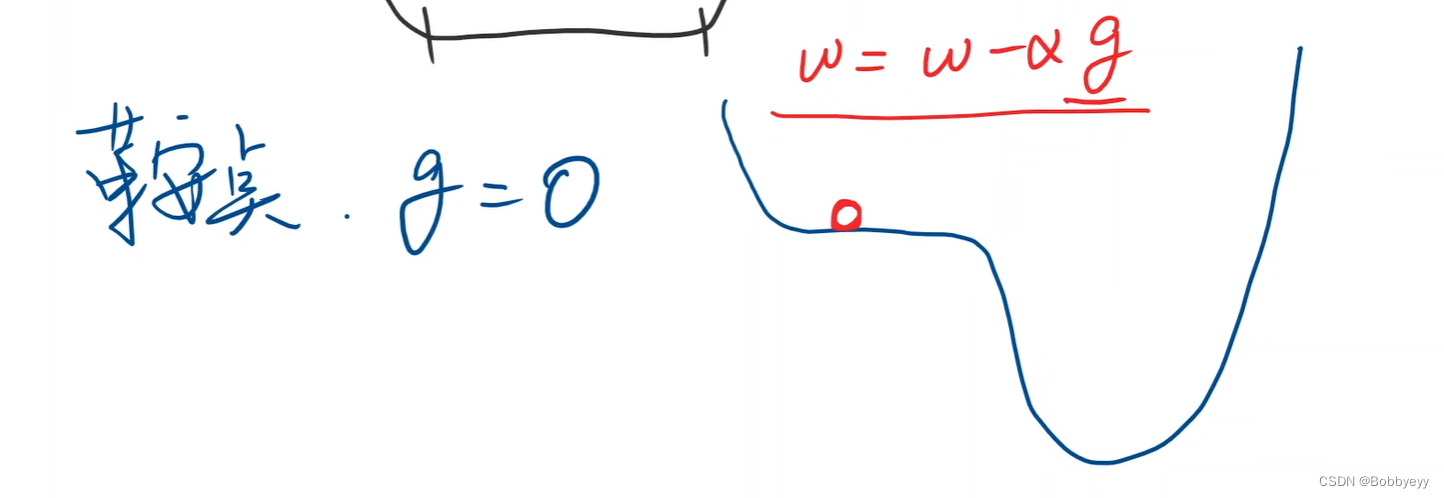
2.5 可以通过指数加权均值平滑cost函数,这样更容易观察曲线趋势。

3 随机梯度下降
3.1 cost在本文中指MSE(所有样本的平均损失),而loss是指单个样本的损失。利用单个样本的loss函数之后增加了随机噪声,可以很大程度上解决鞍点问题。

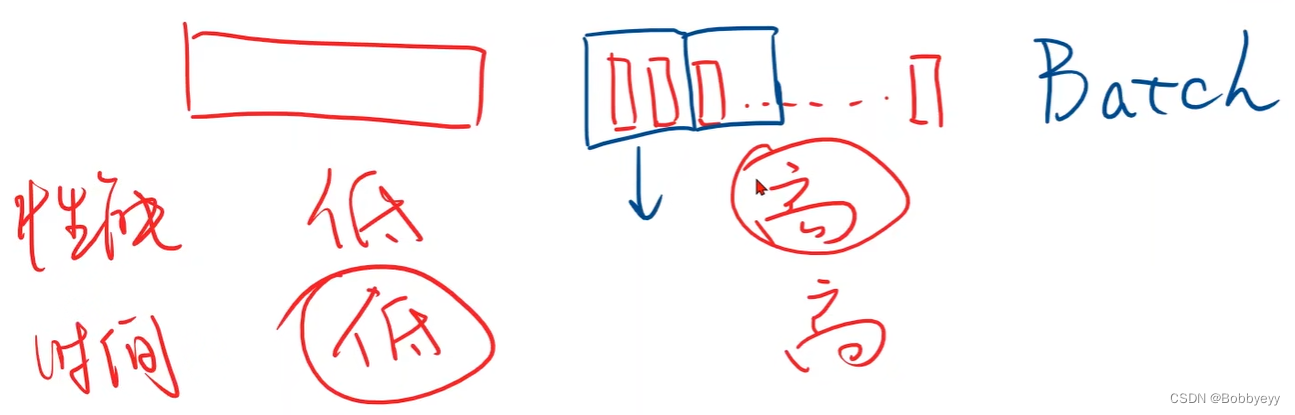
3.2 梯度下降算法每个点的损失计算是可以并行的,但是随机梯度下降算法w的更新依赖于上次w更新的结果。所以梯度下降算法效率更高,随机梯度算法性能更好但是时间复杂度太高。
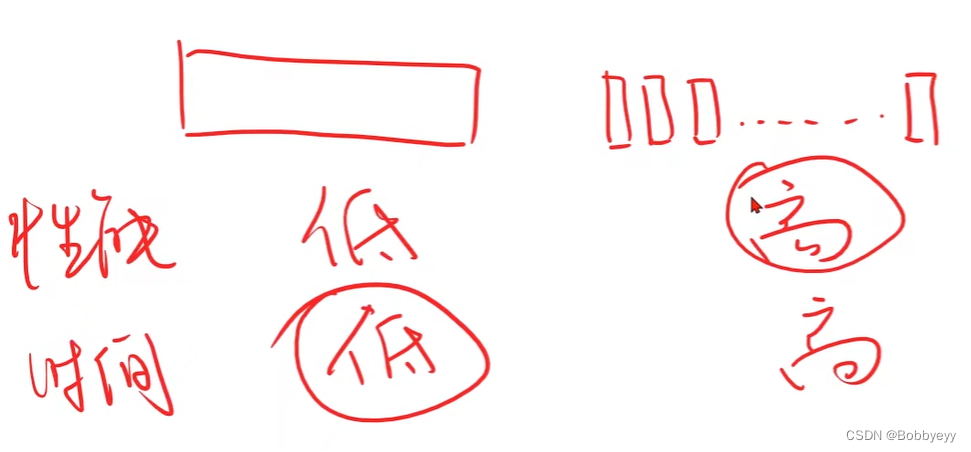
3.3 因此折中引入batch(mini-batch)(批量随机梯度下降)。随机梯度下降法(stochasticgradientdescent,SGD)算法默认使用批量随机梯度下降方法。