1.什么是回溯算法
回溯就是递归问题：
解决组合问题（无顺序），切割问题，子集问题，排列问题（顺序）
所有的回溯可以抽象为一棵树：树 宽度就是for循环大小 树深度就是回溯

void backtracking（参数）
{
  if(终止条件)
  叶子结点收集问题;
  return；
  for（集合元素集）//子节点数 
  处理节点；
  递归函数；
  回溯操作；//有撤销的结果
}

2.组合问题

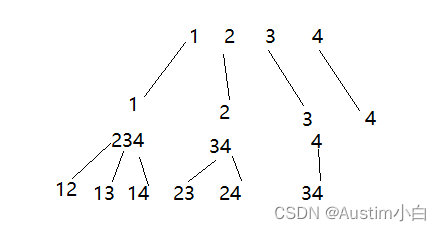
回溯三部曲：
递归函数的参数返回值 : void backtracking(n,k,startindex);n个数4（1234)，k组合大小，startindex 搜索起始位置 一维数组path（12 13 14 等等）二维数组 res
确定终止条件；path.size() == k ;res,push(path);
单层递归逻辑；、
for(i= startindex;i<=n;i++){
path.push();
backtracking(n.k.i+1);
path.pop();//弹出
剪枝

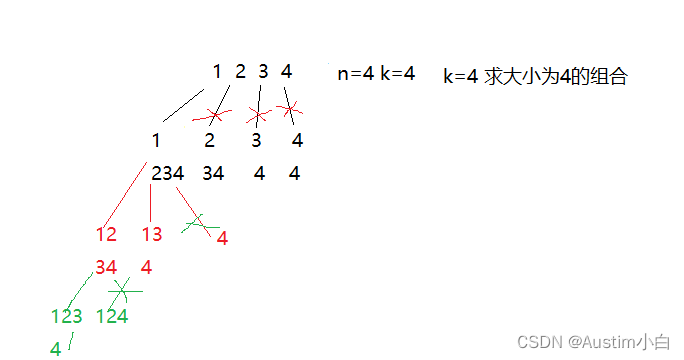
代码：剪枝剪的就是子孩子
for(i = startindex;i<= n-（k-path.size)+1;i++){// 四个子孩子遍历
path.push();
backtracking();//往下搜索过程
path.pop();
}
path.size已经选取的元素大小，还剩k-path.size()个元素要选取；选取的元素至多n-（k-path.size()）+1个；
为什么+1，起始位置包括startIndex;
n = 4； k = 3；path.size() = 0；至多从哪里开始： 4-3+1 =2; 234
题目描述

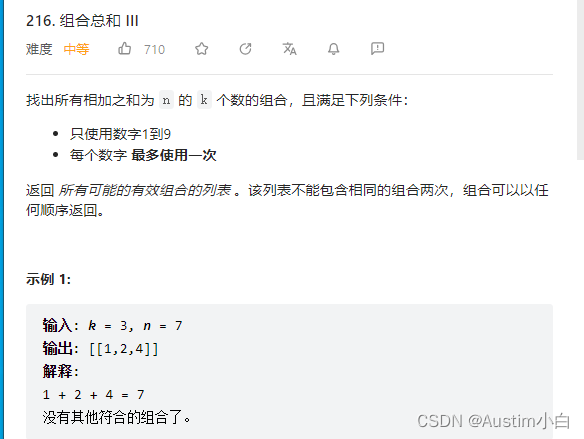
分析：

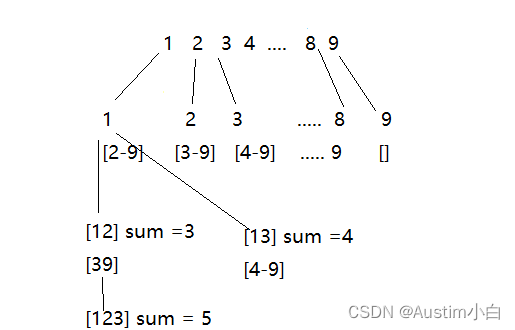
int* path;//一维数组，收集单条路径符合的结果
int path_size;
int** ans;// 二维数组 所有结果集
int ans_size;

void backtrack(int k, int n, int sum, int index)// index比如取2之和，从3开始；开始的时候是1 
{
    // 终止条件 沿途取的个数 == k
    if (path_size == k){// 
        if (sum == n){// sum = n 就是目标结果
            int* temp = (int*) malloc((k + 1)* sizeof(int));
            for (int j = 0; j < k; j++){
                temp[j] = path[j];
            }
            ans[ans_size++] = temp;
        }
        return;
    }
    int i;
    // 取数
    for (i = index; i <= 9; i++) {
        sum += i;//取数 + i
        path[path_size++] = i; //路径 push
        backtrack(k, n, sum, ++index);//
        sum -= i;
        path_size--;//pop 回退
    }
}
int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes)
{
    path = (int*)malloc((k + 1) * sizeof(int));
    ans = (int*)malloc(20 * sizeof(int*));
    path_size = 0;
    ans_size = 0;
    backtrack(k, n, 0, 1);
    *returnSize = ans_size;
    *returnColumnSizes = (int*)malloc(sizeof(int)*ans_size);
    for (int i = 0; i < ans_size; i++){
        (*returnColumnSizes)[i] = k;
    }
    return ans;
}