目录

指数函数及e

指数增长

复数指数

练习

1. expgui

2. 计算e

3 五角星绘制

---

指数函数及e

（1）的比值总是常数

（2）的导数为其自身。（根据比值=1推导出e的值）

%% Plot a^t and its approximate derivative
    a = 2;
    t = 0:.01:2;
    h = .00001;
    y = 2.^t;
    ydot = (2.^(t+h) - 2.^t)/h;
    plot(t,[y; ydot])
    legend('y','dy/dx')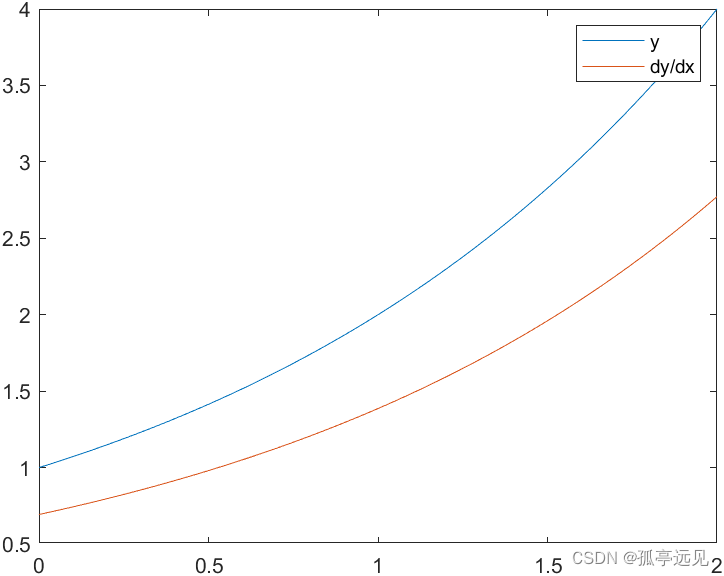

%% Compute e
    format long
    format compact
    h = 1;
    while h > 2*eps
        h = h/2;
        e = (1 + h)^(1/h);
        disp([h e])
    end

对指数函数进行二项式展开，求和式的每一项都通过前一项简单计算得出。该循环在r==s时结束，即两个相连的部分浮点数相同时结束。

%% Experimental version of exp(t)
    t = rand
    s = 1;
    term = 1;
    n = 0;
    r = 0;
    while r ~= s
       r = s;
       n = n + 1;
       term = (t/n)*term;%求和式的每一项都通过前一项简单计算得出
       s = s + term;
    end
    exp_of_t = s

---

指数增长

---

年利、月利、连续利息

%% Compound interest
    fprintf('             t        yearly       monthly     continuous\n')
    format bank
    r = 0.05;
    y0 = 1000;
    for t = 0:20
       y1 = (1+r)^t*y0;
       y2 = (1+r/12)^(12*t)*y0;
       y3 = exp(r*t)*y0;
       disp([t y1 y2 y3])
    end

贷款清还

%% Payments for a car loan
    y0 = 20000
    r = .10
    h = 1/12
    n = 36
    p = (1+r*h)^n/((1+r*h)^n-1)*r*h*y0

---

复数指数

---

绘制八边形

%% Complex exponential
    theta = (1:2:17)'*pi/8
    z = exp(i*theta)
    p = plot(z);
    set(p,'linewidth',4,'color','red')
    axis square off

---

练习

---

1. expgui

---

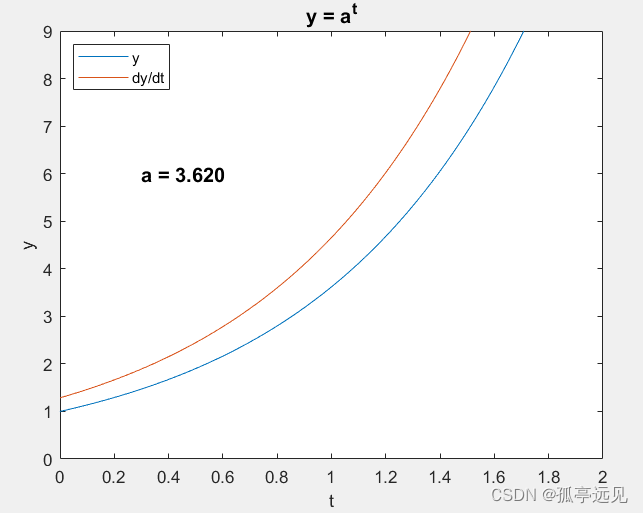
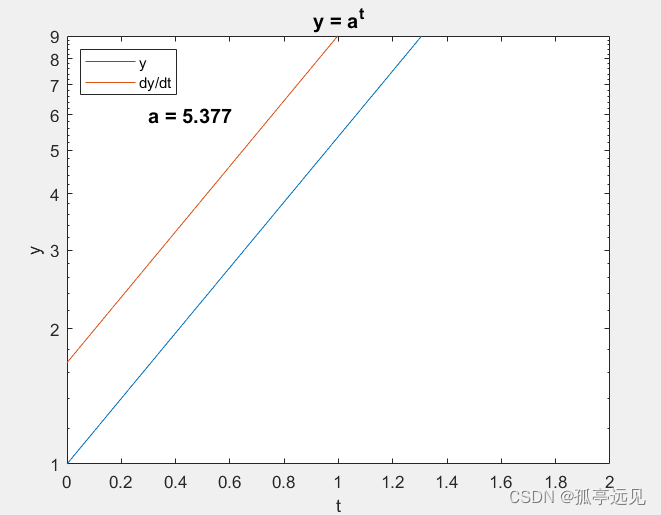
2. 计算e

%% 计算e
%在h很小时，10的负多少次方不能由浮点数很好表示，将会发生偏差
clear
format long
format compact
h=1
while h>1.e-15
    h=h/10; e=(1+h)^(1/h); disp([h e])
end

%% 计算e
clear
format long
format compact
h=1
while h>1.e-15
    h=h/10; e=(1+h)^(1/(1+h-1)); disp([h e])
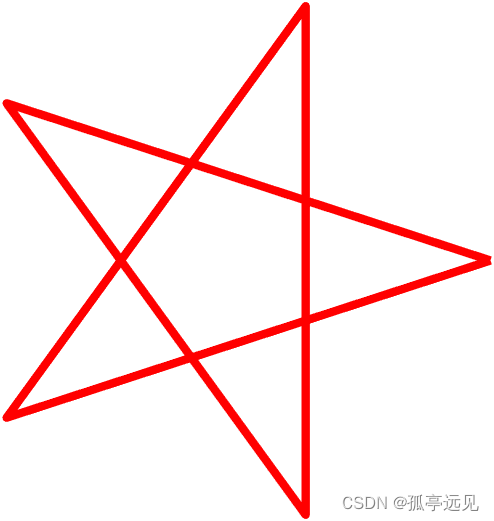
end

---

3 五角星绘制

%% 利用复数指数绘制五角星
    theta = (0:3:15)'*(2*pi/5)
    z = exp(i*theta)
    p = plot(z);
    set(p,'linewidth',4,'color','red')
    axis square off