目录
一,插入排序
二,希尔排序
三,选择排序
四,冒泡排序
五,快排
5.1 Hoare法
5.2 挖坑法
5.3 指针法
5.4 非递归写法
六,归并排序
6.1 递归
6.2 非递归
一,插入排序
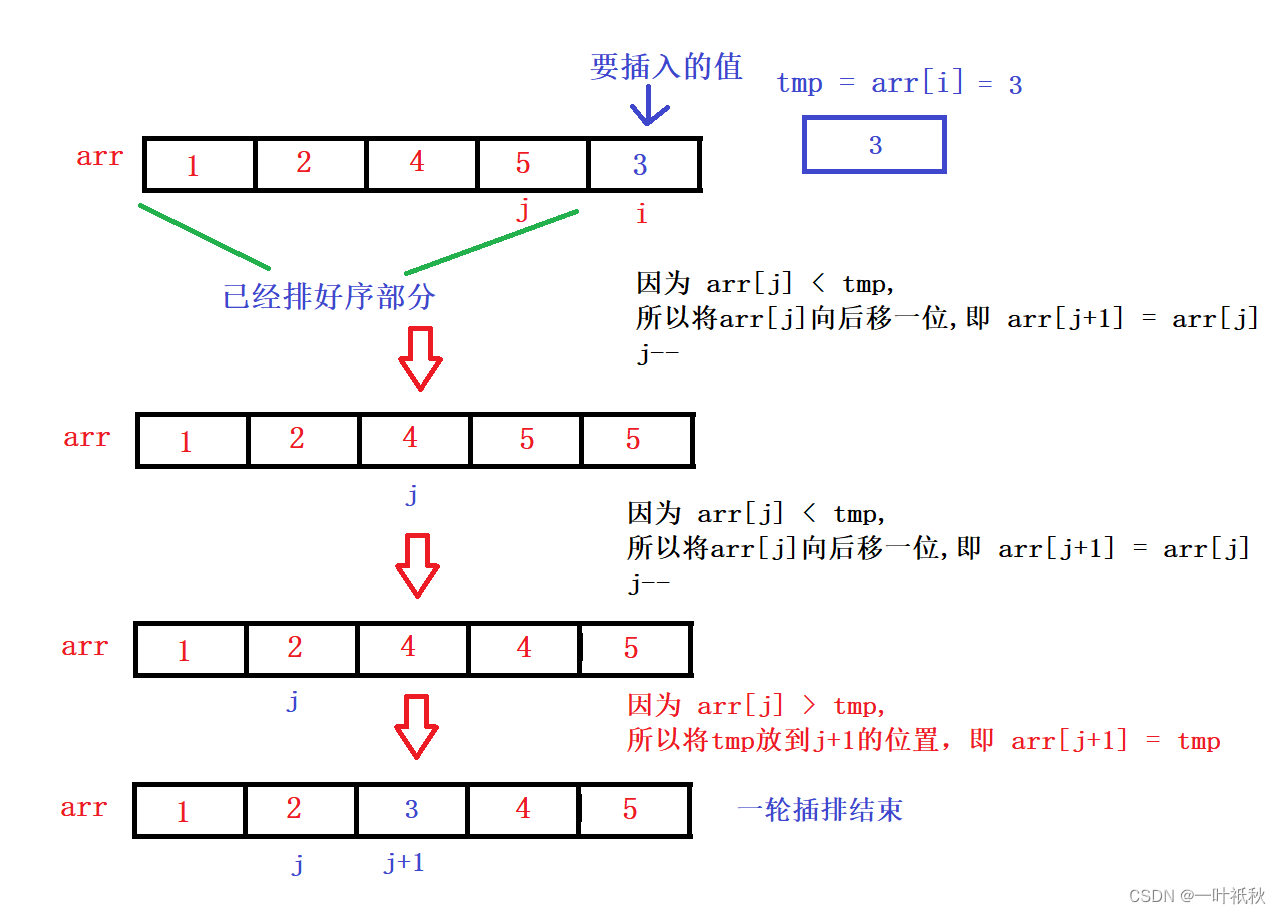
基本思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
/**
* 直接插入排序
* 时间复杂度:O(n^2)
* 空间复杂度:O(1)
* 稳定性:稳定
*/
public void insertSort(int[] arr){
for (int i = 1; i < arr.length; i++) {
int tmp = arr[i];//要插入的元素
int j = i-1;
for (; j >= 0; j--) {
if(arr[j] > tmp){//判断是否插入
arr[j+1] = arr[j];
}else{
break;
}
}
arr[j+1] = tmp;
}
}二,希尔排序
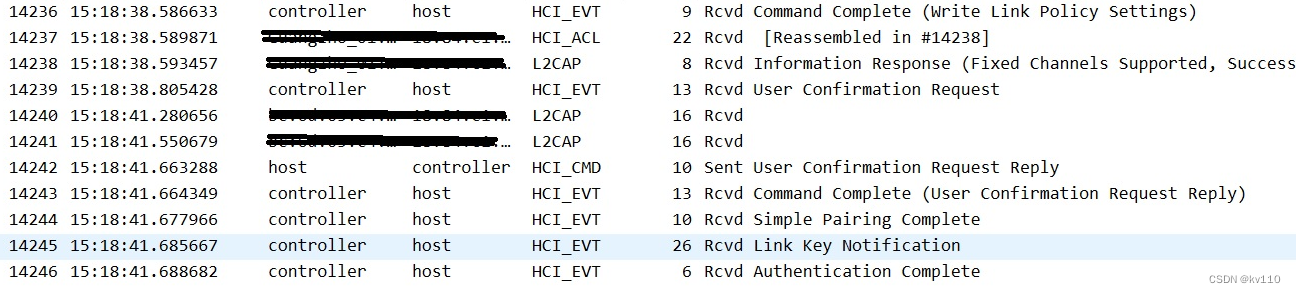
基本思想:先选定一个整数,把待排序文件中所有记录分成多个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后gap/=2,重复上述分组和排序的工作。当到达gap=1时,所有记录在统一组内排好序。画个图理解一下:

/**
* 希尔排序 - 直接排序的优化版
* 时间复杂度:O(n^1.3)~O(1^1.5)
* 空间复杂度:O(1)
* 稳点性:不稳定
*/
public void shellSort(int[] arr){
int gap = arr.length;
while(gap > 1){
gap /= 2;
for (int i = gap; i < arr.length; i++) {
int tmp = arr[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if(arr[j] > tmp){
arr[j+gap] = arr[j];
}else{
break;
}
}
arr[j+gap] = tmp;
}
}
}
三,选择排序
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
/**
* 选择排序
* 时间复杂度:O(n^2)
* 空间复杂度:O(1)
* 稳定性:不稳定
*/
public void selectSort(int[] arr){
for (int i = 0; i < arr.length; i++) {
int minIndex = i;
for (int j = i+1; j < arr.length; j++) {
if(arr[minIndex] > arr[j]){
minIndex = j;
}
}
swap(arr,minIndex,i);
}
}
public void swap(int[] arr, int i, int j){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
四,冒泡排序
基本思想:根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
/**
* 冒泡排序
* 时间复杂度:O(n^2)
* 空间复杂度:O(1)
* 稳定性:稳定
*/
public void bubbleSort(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
boolean flg = true;
for (int j = 0; j < arr.length-1-i; j++) {
if(arr[j] > arr[j+1]){
int tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
flg = false;
}
}
if(flg){
break;
}
}
}五,快排
基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
5.1 Hoare法

从整体看,这就像一颗二叉树,所以我们可以用类似二叉树遍历的递归来实现,代码如下:
/**
* 快排
* 时间复杂度:O(nlogN)
* 空间复杂度:O(logN)
* 稳定性:不稳定
*/
public void quickSort(int[] arr, int left, int right){
if(left > right) return;//递归终止条件
int div = partition(arr, left, right);//得到基准值下标
quickSort(arr,left,div-1);//递归基准值前面的值
quickSort(arr,div+1,right);//递归基准值后面的值
}
public int partition(int[] arr, int left, int right){
int tmp = left;
int key = arr[left];
while(left < right){
//注意这里只能先遍历右边,否则基准值的前面就会存在 >基准值的值,
//后面就会存在 <基准值的值
// && = 号必须有,不然如果基准和R相同,就会出现死循环
while(left < right && arr[right] >= key){
right--;
}
while(left < right && arr[left] <= key){
left++;
}
swap(arr,left,right);
}
swap(arr,tmp,left);
return left;//or right
}5.2 挖坑法
与Hoare法类似,只不过它把基准的初始位置当作一个坑,查找右边,将右边的值赋给坑,将右边变成坑,再查找左边,将左边的值赋给坑,将左边变成坑,重复以上操作直到 L== R,将arr[L] = key。再往下面递归,这里就不画图讲解了,直接上代码:
public int partition(int[] arr, int left, int right){
int tmp = arr[left];
while(left < right){
while(left < right && arr[right] >= tmp){//=必须有 , 必须是right先走
right--;
}
arr[left] = arr[right];
while(left < right && arr[left] <= tmp){
left++;
}
arr[right] = arr[left];
}
arr[left] = tmp;
return left;
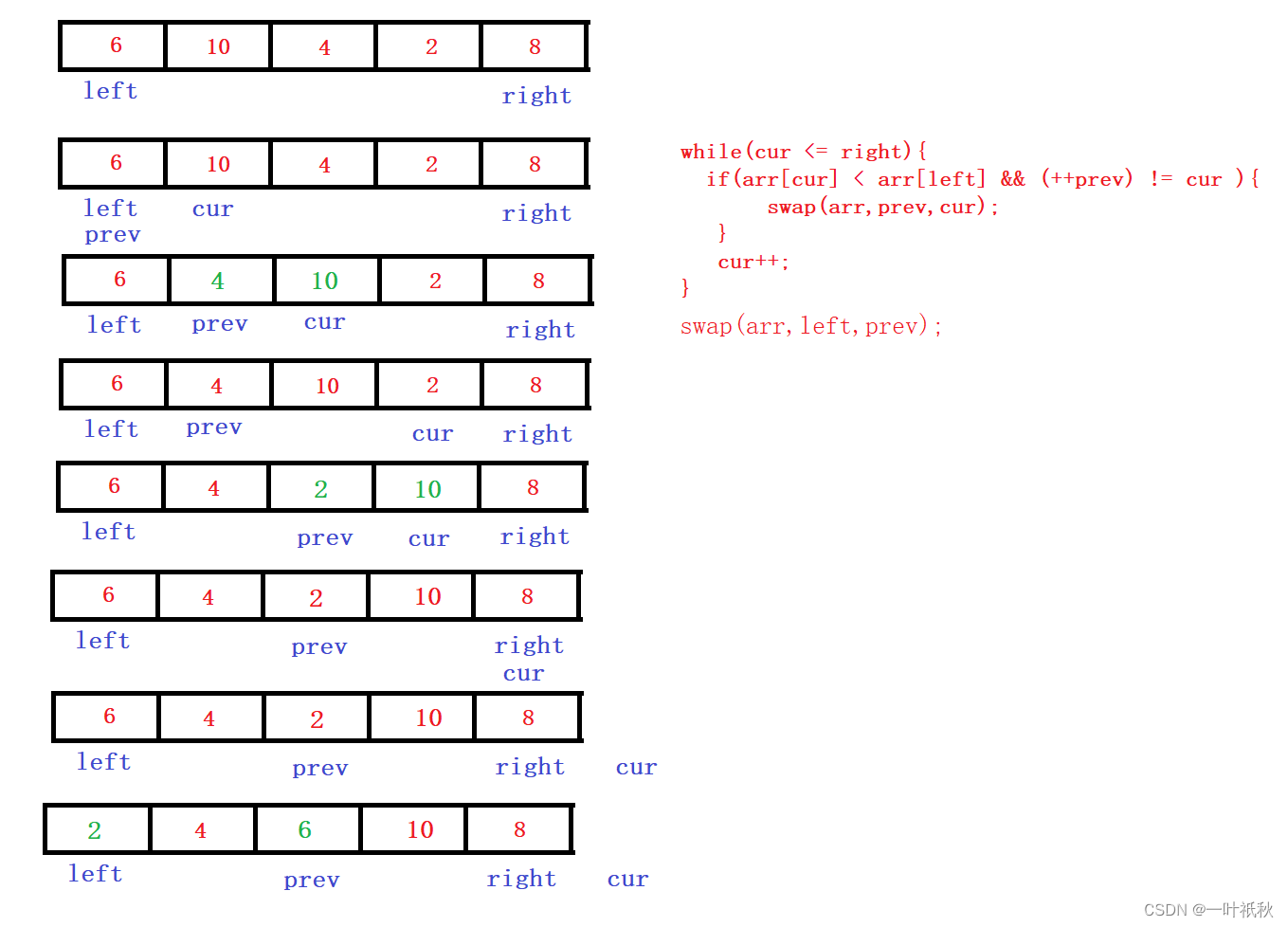
}5.3 指针法
它的主要思想没变,还是找到基准值的下标位置,将其分成两份,依次类推,但是它寻找基准的方法很神奇,先看代码:
public int partition(int[] arr, int left, int right){
int prev = left;
int cur = left + 1;
while(cur <= right){
if(arr[cur] < arr[left] && (++prev) != cur ){
swap(arr,prev,cur);
}
cur++;
}
swap(arr,left,prev);
return prev;
}
5.4 非递归写法
public void quickSortNor(int[] arr, int left, int right){
Stack<Integer> ret = new Stack<>();
ret.push(left);
ret.push(right);
while(!ret.empty()){
right = ret.pop();
left = ret.pop();
int div = partition(arr,left,right);//找到基准的下标
if(left + 1 < div){//基准左边有2+的元素
ret.push(left);
ret.push(div-1);
}
if(right-1 > div){//基准右边有2+的元素
ret.push(div+1);
ret.push(right);
}
}
}六,归并排序
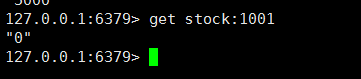
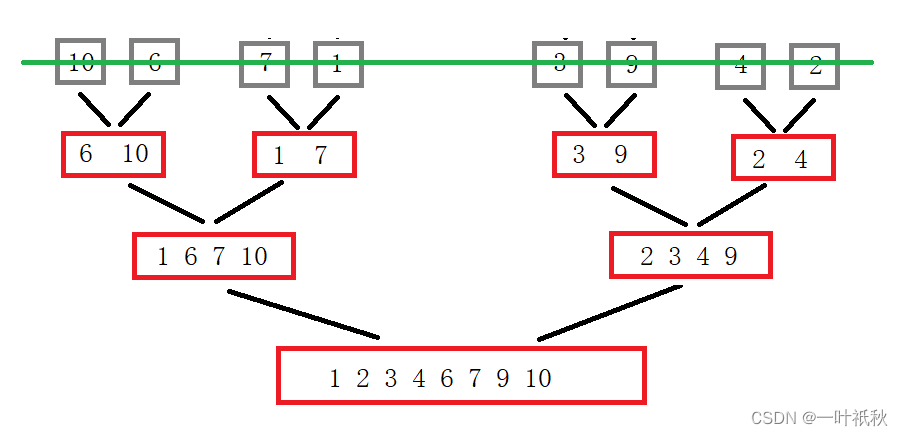
基本思路:将一组数据分成等长的两份,再将每份分成等长的两份,直到每份数据的长度都为一,然后再逆推回去,每次逆推都要进行一次排序,直到变成一份。如图:

6.1 递归
可以通过子问题的思路来理解代码:先将前面的一半排序,再将后面的一半排序,最后将整体排序,它们的每一部分都可是这样操作,所以可以使用递归解决。
/**
* 归并排序
* 时间复杂度:O(nlogn)
* 空间复杂度:O(n)
* 稳定
*/
public void mergeSort(int[] arr, int left, int right){
if(left >= right) return;
int mid = left + (right - left)/2;
mergeSort(arr,left,mid);// 前 n/2 排序
mergeSort(arr,mid+1,right);// 后 n/2 排序
merge(arr,left,right,mid);// 整体排序
}
public void merge(int[] arr, int left, int right, int mid){
int s1 = left;
int s2 = mid+1;
int k = 0;
int[] tmp = new int[right-left+1];
while(s1 <= mid && s2 <= right){
if(arr[s1] <= arr[s2]){
tmp[k++] = arr[s1++];
}else{
tmp[k++] = arr[s2++];
}
}
while(s1 <= mid){
tmp[k++] = arr[s1++];
}
while (s2 <= right){
tmp[k++] = arr[s2++];
}
for (int i = 0; i < tmp.length; i++) {
arr[i+left] = tmp[i];
}
}6.2 非递归
思路:直接将其分成一个一组,然后再两两组合,直到合成一体,就只有上面那张图的下半部分:
public void mergeSortNor(int[] arr){
int gap = 1;
while(gap < arr.length){
for (int i = 0; i < arr.length; i+=2*gap) {
int left = i;//相邻两段子数组的开始和末位下标 [left,mid] [mid+1,right]
int mid = left + gap -1;
int right = mid + gap;
if(mid >= arr.length){//说明只有前面一段数组
mid = arr.length - 1;
}
if(right >= arr.length){//说明后面的子数组数量少
right = arr.length-1;
}
merge(arr,left,right,mid);
}
gap *= 2;
}
}